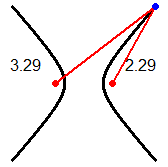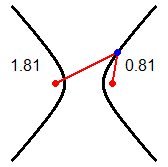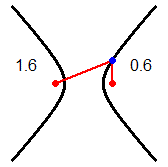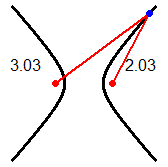
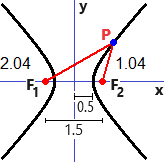
Una iperbole è l'insieme dei punti del piano le cui distanze da due punti fissati (detti fuochi) hanno differenza costante.  Nel nostro caso:  1.25-0.25 = 1.3-0.3 = 1.42-0.42 = ... = 1.  La distanza tra i fuochi è 1.5.  La distanza tra i due rami dell'iperbole è 1.

Posso tracciare l'iperbole con WolframAlpha:
      hyperbola center (0, 0), focus (0.75, 0), vertex (0.5,0)
foci | (0.75, 0) | (-0.75, 0)
vertices | (0.5, 0) | (-0.5, 0)
semimajor axis length | 0.5
semiminor axis length | 0.559017
focal parameter | 0.416667
eccentricity | 1.5
asymptotes | y = 1.11803 x + 0 | y = 0 - 1.11803 x
  Equivale a:
     

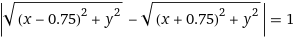
Nel caso particolare in cui gli asintoti siano uno verticale e l'altro orizzontale un'iperbole può essere interpretata come grafico di una funzione. Esempio:
hyperbola center (0, 0), focus (1, 1), semimajor axis length = 1

È il grafico di  x → 1/(2·x) plot y-1/(2*x) = 0    → intersect y = 1/(2*x), y = x   x = -1/sqrt(2), y = -1/sqrt(2)   x = 1/sqrt(2), y = 1/sqrt(2)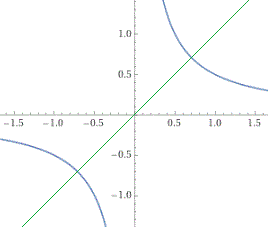