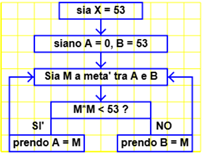
Considera il diagramma di flusso rappresentato qui a lato.  Cerca di capire come si comporta la sequenza di numeri che viene generata se prendiamo come X un numero maggiore di 1.  Fallo utilizzando il programmino che viene avviato se premi QUI.

leggi X | A = 0 B = X | ---> M = (A+B)/2 <--- | | | | M×M < X ? | | sì | | no | | | | | ---- A = M B = M ----

Un esempio:

X = 53
A = 0   B = 53  (A+B)/2 = 26.5
A = 0   B = 26.5  (A+B)/2 = 13.25
A = 0   B = 13.25  (A+B)/2 = 6.625
A = 6.625   B = 13.25  (A+B)/2 = 9.9375
A = 6.625   B = 9.9375  (A+B)/2 = 8.28125
...
A = 7.280109889280517   B = 7.280109889280523  (A+B)/2 = 7.280109889280521
A = 7.280109889280517   B = 7.280109889280521  (A+B)/2 = 7.280109889280519
A = 7.280109889280517   B = 7.280109889280519  (A+B)/2 = 7.280109889280518
A = 7.280109889280517   B = 7.280109889280518  (A+B)/2 = 7.280109889280517
A = 7.280109889280517   B = 7.280109889280518  (A+B)/2 = 7.280109889280517
...

Prova altre volte, e osserva in particolare cosa accade se X è 4, 9, 16, 25, 36, 49, 64 o 81.

Prova, infine, a prendere il numero K su cui si sono stabilizzare le uscite e a calcolare K×K.

Nel caso dell'esempio fatto sopra otteniamo 7.280109889×7.280109889 = 53

È facile concludere che questo programmino calcola la radice quadrata di X.

Questo è uno dei molti programmini che possono essere utilizzati per ottenere la radice quadrata di un numero.  Le calcolatrici utilizzano dei metodi di calcolo di questo tipo per calcolare operazioni più complicate della quattro operazioni.