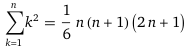Verifica col computer che per n intero positivo 1² + 2² + 3² +…+ n² = n·(n+1)·(2·n+1)/6.

Un modo molto semplice è usare una calcolatrice, ad es. la calcolatrice online "calcolatrice2" presente qui.  Impiegando il tasto [N] posso generare sequenze qualunque di numeri naturali, con [data^Q] (Q = 2) posso elevarli al quadrato, con [sum] posso farne la somma.  Ad esempio se n = 12 metto 12 nel riquadro sopra [N] e premo questo tasto; poi metto 2 in Q e premo [data^Q], in modo da ottenere da ottenere i primi 12 interi positivi elevati al quadrato; poi copio questa sequenza di numeri sopra a [N] e premo [sum] ottenendone la somma, 650.  Lo stesso risultato lo ottengo calcolando 12·(12+1)·(2·12+1)/6.

Analogamente, ad esempio per n = 30, ottengo:  1+4+9+...+841+900 = 9455;   30*(30+1)*(2*30+1) = 9455

    Ovviamente potrei ricorrere al software online WolframAlpha introducendo  1^2+2^2+3^2+ ... +n^2

 

    Ma situazione può essere affrontata anche con un semplicissimo programma in Basic (o in un altro linguaggio di programmazione):

10 input "N = "; N
20 s = 0
30 for i = 1 to N : s=s+i^2 : next
40 print "1^2+2^2+ ... +N^2 = "; s
50 print "N*(N+1)*(2*N+1)/6 = "; N*(N+1)*(2*N+1)/6
60 goto 10

N =  10
1^2+2^2+ ... +N^2 = 385
N*(N+1)*(2*N+1)/6 = 385
N =  30
1^2+2^2+ ... +N^2 = 9455
N*(N+1)*(2*N+1)/6 = 9455
N =  100
1^2+2^2+ ... +N^2 = 338350
N*(N+1)*(2*N+1)/6 = 338350