Trova come semplificare il calcolo del prodotto (1-1/2)(1-1/3)(1-1/4)...(1-1/n) con una formula e dimostra la cosa per induzione.

Facciamo qualche prova, ad esempio con la "piccolissima" calcolatrice online presente qui:

(1-1/2)*(1-1/3)*(1-1/4)*(1-1/5) = 0.2
(1-1/2)*(1-1/3)*(1-1/4)*(1-1/5)*(1-1/6)*(1-1/7)*(1-1/8) = 0.125
(1-1/2)*(1-1/3)*(1-1/4)*(1-1/5)*(1-1/6)*(1-1/7)*(1-1/8)*(1-1/9)*(1-1/10) = 0.1

È facile congetturare che (1-1/2)(1-1/3)(1-1/4)...(1-1/n) = 1/n.

Posso verificare la cosa con WolframAlpha:

(1-1/2)*(1-1/3)*(1-1/4)*...*(1-1/n)   →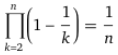

Proviamo a dimostrarlo per induzione.

Passo inziale: (1-1/2) = 1/2   OK
Supponiamo che (1-1/2)(1-1/3)...(1-1/n) = 1/n;
(1-1/2)(1-1/3)...(1-1/n)(1-1/(n+1)) = 1/n·(1-1/(n+1)) = 1/n·(n+1-1)/(n+1) = 1/n·n/(n+1) = 1/(n+1)   OK