Risolvi rispetto a x (eventualmente in modo approssimato) la disequazione (x + 1)³ − x > 0.

Mi conviene trasformare la disequazione in:   (x + 1)³ > x
e affrontare questa schizzando le curve y=(x + 1)³ (che so ottenere traslando il grafico di y=x³) e y=x.
y=(x + 1)³ a destra di x=0 sta sopra ad y=x in quanto per x>0  (x+1)³ > x+1 > x  (l'elevamento al cubo di un numero maggiore di 1 è maggiore del numero di partenza).
    A sinistra di x=0 il primo grafico scavalca il secondo in un punto di ascissa k compresa tra -3 e -2 (il primo in -2 ha ordinata -1 e in -3 ha ordinata -8): si tratta dell'unica intersezione tra i due grafici.
    Quindi le soluzioni sono gli elementi dell'intervallo (k,∞). Sotto la rappresentazione grafica, tracciata col computer ma schizzabile a mano.

Per trovare k con più precisione posso procedere per approssimazioni successive, usando una calcolatrice per tabulare (x + 1)³ o ricorrendo ad un apposito programma. Ad esempio posso usare lo script online "equazioni" presente qui, dopo aver sviluppato il termine nella forma x^3 + 3*x^2 + 2*x + 1.

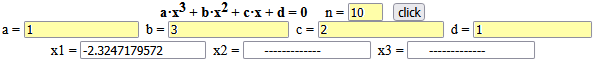
Per altri commenti: disequazioni negli Oggetti Matematici

In alternativa si può ricorrere a questo semplice script online, riscritta la disequazione come:  x^3 + 3*x^2 + 2*x + 1 > 0.

La rappresentazione grafica è stata realizzata con questo script (vedi QUI esempi analoghi).