Ad una azienda tessile viene richiesto di produrre un tessuto che deve contenere cotone e almeno 25 kg di filo sintetico e 45 kg di lana. L'azienda può usare una miscela di due filati, così costituiti: (1) cotone 20%, sintetico 50%, lana 30%, o: (2) cotone 30%, sintetico 10%, lana 60%. Sia m la moneta corrente. Il filato (1) costa 30 m/kg, il filato (2) 20 m/kg. In quali quantità deve utilizzare i due filati per minimizzare i costi? Risolvi il problema "geometricamente".
Siano x ed y i due tipi di filato. Il problema è:
| 0.5 x + 0.1 y ≥ 25 | |
| 0.3 x + 0.6 y ≥ 45 | |
| x + 0y ≥ 0 | |
| 0x + y ≥ 0 |
WolframAlpha con:
minimize[30x+20y, {0.5x+0.1y>=25 && 0.3x+0.6y >= 45 && y>=0 && 0<=x} ]
fornisce min ≈ 2277.78 at (x,y) ≈ (38.8889, 55.5556)
Mi conviene prendere 38.9 kg del primo filato e 55.6 kg del secondo.
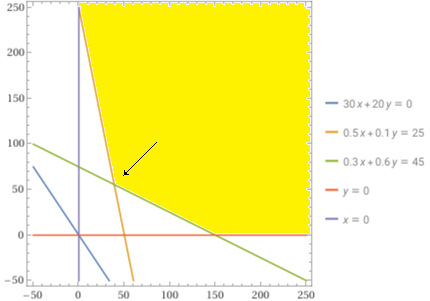
La regione e la retta 30 x + 20 y = 0:
plot 30x+20y=0, 0.5x+0.1y=25, 0.3x+0.6y = 45, y=0 , x=0, -50 < x < 250, -50 < y < 250
Approfondimenti in:
Programmazione lineare neGli Oggetti Matematici.