Un proiettile è lanciato da terra verso l'alto, verticalmente. Se la sua altezza H in metri in funzione del tempo t (in secondi) trascorso dal lancio è data dalla formula  H = 45 t – 4.9 t²,  qual era la velocità di lancio? qual è l'altezza massima raggiunta dal proiettile? qual è la velocità che aveva quando ha toccato terra?

• H(t) è polinomio di 2° grado in t con coefficiente direttivo negativo.
H'(t) = D_t(45 t – 4.9t²) = 45 – 9.8 t
La velocità iniziale è H'(0) = 45 (m/s).

• L'altezza smette di crescere quando H'(t)=0, ossia per t = 45/9.8.
In tale istante H = 45·45/9.8 – 4.9(45/9.8)² = 45·45/9.8(1 – 4.9/9.8) = 45·45/9.8/2 = 103.31…, che arrotondo a 103 (m).

• Il proiettile è a terra quando H=0, ossia 45 t – 4.9t² = t(45 t – 4.9t) = 0. Una soluzione è t=0 (lancio), l'altra è t = 45/4.9. In tale istante la velocità con cui varia H è 45 – 9.8·45/4.9 = 45 – 90 = –45:
stesso valore assoluto e segno opposto rispetto alla velocità di lancio.
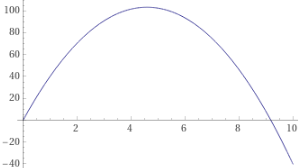
È quanto ci dovevamo aspettare tenendo conto che il grafico di H = 45 t – 4.9t² è simmetrico rispetto alla retta passante per il vertice: la pendenza della tangente nei punti di intersezione con l'asse x deve essere opposta.

Grafico e calcoli col software online WolframAlpha. Vedi qui.

plot 45*t - 4.9*t^2, 0 < t < 10

d/dt 45*t - 4.9*t^2, t=0
      45  (vel. inziale di lancio)
maximize 45*t - 4.9*t^2
     max = 10125/98 at t = 225/49
     max ≈  103.32 at t  ≈  4.5918  (alt. massima)
solve 45*t - 4.9*t^2 = 0
t = 450/490 ≈ 9.1837  (quando tocca terra)
d/dt 45*t - 4.9*t^2, t=450/49
      -45  (vel. quando tocca terra, opposta a quella di partenza)
    Potevo trovare il massimo anche trovando dove si azzera la deriv.
solve (d/dt 45*t - 4.9*t^2=0) for t
      t = 225/49
45*t - 4.9*t^2, t = 225/49
      103.316