Tracciare il grafico di x → asin(x)+acos(x) [con asin, acos, atan si indicano le funzioni "arcoseno", "arcocoseno" e "arcotangente", ossia le funzioni inverse di sin, cos e tan ristrette al massimo intervallo contenente [0,π/2) in cui sono iniettive].

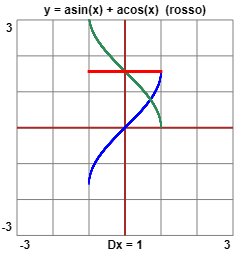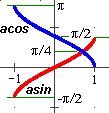
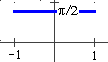
Sia asin che acos hanno come dominio [-1,1], ossia l'immagine delle funzioni sin e cos. Quindi questo è anche il dominio di asin+acos. Se si tracciano i grafici di asin e acos (simmetrici rispetto a y=x di quelli di sin e cos, ristretti come ricordato nel testo) si capisce subito che sono tra loro simmetrici rispetto a una retta orizzontale e che quindi la loro funzione somma è costante e vale, ad es., asin(0)+acos(0) = 0+π/2 = π/2. 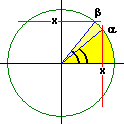Si poteva arrivare a questa conclusione anche ragionando sul cerchio di centro O e raggio 1: l'arcocoseno di x e l'arcoseno di x sono direzioni α e β tra loro simmetriche rispetto a y=x, ovvero sono angoli tra loro complementari (aventi per somma π/2).

Il grafico con questo script per controllare la risposta: