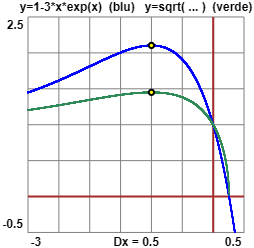
P = √(1 – 3 T e^T) per quale valore di T ha il valore massimo?

Invece che derivare P in funzione di T ci conviene osservare che la radice quadrata è una funzione crescente, quindi conserva la crescenza/decrescenza della funzione a cui viene applicata. Possiamo quindi ricondurci a trovare il massimo di 1 – 3 T eT, restringendoci ai T in cui tale termine non è negativo.

d(1–3TeT)/dT = 0 – 3·(1·eT + T·eT) = –3eT(1+T) ha segno opposto a quello di T+1 in quanto eT>0. Dunque 1–3TeT cresce per T≤–1 e decresce per T≥–1, e assume in –1 il valore massimo, pari a 1+3e–1. Questo valore è maggiore di 0 e quindi appartiene al dominio di √(1–3TeT). Anche questo termine assume quindi valore massimo per T = –1. A lato sono tracciati i grafici in funzione di T sia di 1–3TeT che di √(1–3TeT).