Calcolare (motivando) g'(1) dove g è la funzione inversa di f così definita:
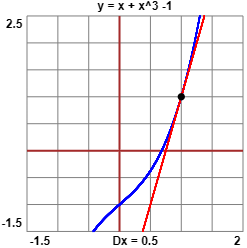
(a)  f(x) = x + x³ − 1
f è invertibile in tutto R, infatti è la somma di due funzioni crescenti e una funzione costante; f(x) = 1 per x = 1; quindi:
D _y=1 (g(y)) = 1/D _x=1 (f(x)) = [1/(1+3x²)] _x=1 = 1/4.
In figura, a conferma, si vede che nel punto di ordinata (e ascissa) 1 il grafico di f ha pendenza 4.

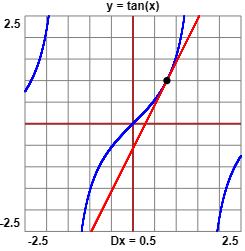
(b)  f(x) = tan(x)
f è invertibile in ciascun intervallo di ampiezza π centrato in nπ al variare di n in N; per l'inversa in (-π/2, π/2) o in qualunque altro di questi intervalli, essendo l'andamento periodico, dovremmo trovare la stessa derivata nel punto 2, uguale al reciproco della pendenza del grafico della funzione tangente nel punto di ordinata 2.
In (-π/2, π/2) tan(x)=1 per x = π/4:
D_y=1 (g(y)) = 1/D_x=π/4 (f(x)) = [1/(1+tan(x)²)]_x=π/4 = 1/2  (si vede che nel punto il grafico di f ha pendenza 2)
Operando in un qualunque altro intervallo avremmo ottenuto lo stesso valore (sarebbe stato diverso il valore di x per cui tan vale 1, ma 1+tan(x)² avrebbe comunque avuto valore 2).

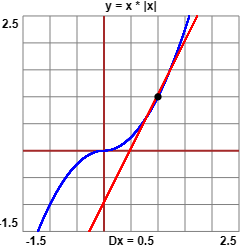
(c)  f(x) = x·|x|
f è crescente e quindi invertibile in tutto R in quanto per x ≥ 0 si comporta come x² e per x ≤ 0 come -x².
f(x) = 1 per x=1, dove f(x) = x²
D_y=1 (g(y)) = 1/D_x=1 (f(x)) = [1/(2x)]_x=1 = 1/2  (si vede che nel punto il grafico di f ha pendenza 2).

Richiami qui.  I grafici sono stati fatti con gli script uno, due, tre.