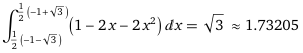Controlla la risposta con WolframAlpha.
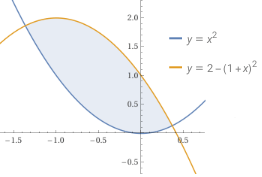
La parabola verde è y = -x² traslata di Δx = -1 e Δy = 2, ossia y = -(x+1)²+2.
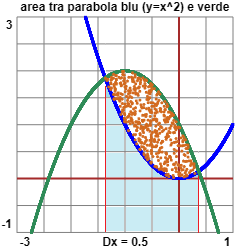
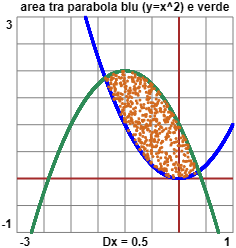
| Calcola
l'area delle figura rappresentata a fianco, compresa tra la parabola
y = x² e la parabola, uguale, ma ruotata di 180°, avente vertice in (-1.5,2). Controlla la risposta con WolframAlpha. | |
| La parabola verde è y = -x² traslata di Δx = -1 e Δy = 2, ossia y = -(x+1)²+2. |
Le due parabole si intersecano nei punti che hanno per ascissa le soluzioni di
-(x+1)²+2 = x², ossia di 2x²+2x-1=0:
x1 = -1/2-√3/2 = - 1.36…, x2 = -1/2+√3/2 = 0.36…
Indichiamo con I l'intervallo [x1,x2]; l'area cercata sta tra questi due valori di x e
"sta sotto a y = -(x+1)²+2"
ma "non sta sotto a y = x²"
∫[-1/2-√3/2,-1/2+√3/2] -(x+1)²+2 dx - ∫[-1/2-√3/2,-1/2+√3/2] x² dx =
∫[-1/2-√3/2,-1/2+√3/2] 2x²+2x-1 dx =
[l'antiderivata di 2x²+2x-1 è -2/3 x³ - x²+ x]
(-2/3 x³ - x²+ x)x=-1/2+√3/2 - (-2/3 x³ - x²+ x)x=-1/2-√3/2 =
1.7320508075688776
Manipolando potrei arrivare direttamente alla soluzione √3 = 1.73…
Potrei fare il calcolo anche con
la "calcolatrice" presente QUI:
-2/3*pow(A,3)-pow(A,2)+A per A = -1/2 [+] sqrt(3)/2 → 0.3660254037844386 (risultato messo automaticamente in A)
0.19935873711777197
-2/3*pow(A,3)-pow(A,2)+A per A = -1/2 [-] (sqrt(3)/2) = -1.3660254037844386 (risultato messo automaticamente in A)
0.3660254037844386 - (-1.3660254037844386) → 1.7320508075688776
Con WolframAlpha è tutto molto semplice. Metto in input:
area between y = x^2 and y = -(x+1)^2+2 e ottengo:
Potrei fare il calcolo anche con un programmino, ad esempio in Basic:
10 a = -1/2-sqr(3)/2 : b = -1/2+sqr(3)/2 : d = b-a ... 500 y = 2*(x^2)+2*x-1 : return n = 4321 integrale = -1.7320508539522268 n = 8642 integrale = -1.732050819164719 variaz.= 3.4787507763311964e-8 n = 17284 integrale = -1.7320508104678345 variaz.= 8.69688454585571e-9 n = 34568 integrale = -1.7320508082936124 variaz.= 2.1742221356646496e-9 n = 69136 integrale = -1.7320508077500738 variaz.= 5.435385475038856e-10 n = 138272 integrale = -1.7320508076141847 variaz.= 1.358890777680699e-10 n = 276544 integrale = -1.732050807580238 variaz.= 3.3946623290148636e-11