Trova la derivata rispetto a x di x·e^x.  Determina quindi, aiutandoti col precedente risultato,  ∫ x·e^x dx.  Trova, infine,  ₀∫^∞ x·e^{− x} dx.

D_x(x·e^x) = e^x + x·e^x.
Quindi  D_x(x·e^x − e^x) = e^x + x·e^x − e^x = x·e^x.
Dunque  ∫x·e^x dx = x·e^x − e^x + c, al variare di c tra i numeri reali.
Allora  ₀∫^∞ x·e^{− x} dx = − ₀∫^−∞ (−u)·e^u du = [ho cambiato −x con u e, quindi, ho cambiato anche gli estremi di integrazione e ho cambiato segno all'integrale] = ₀∫^−∞ u·e^u du =  [u·e^u − e^u] _u=−∞ − [u·e^u − e^u] _u=0  =  0 − 0 − 0 − (−1)  =  1.
    Quindi  x → x·e^{− x}   (di cui sotto a sinistra è tracciato, parzialmente, il grafico tra 0 e ∞:  in questo intervallo la funzione è positiva, tranne che in 0, dove è nulla;  ha per derivata  x → e^{− x}(1 − x)  che è positiva in [0,1), negativa in (1,∞) e nulla in 1;  e tende a 0 al tendere dell'input a ∞)   è una candidata ad essere una funzione di densità tra 0 e ∞.

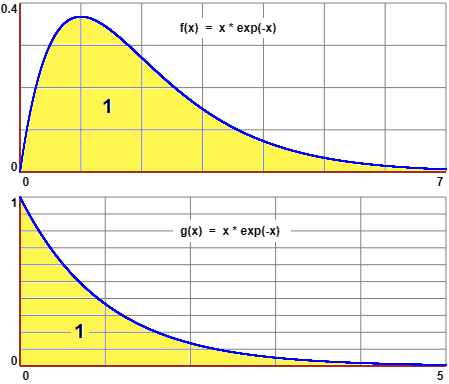
Tuttavia, poichè anche  ₀∫^∞ e^{− x} dx = 1,  pure  x → e^{− x}  (di cui sopra a destra è tracciato, parzialmente, il grafico)   è una funzione densità tra 0 e ∞, come lo è più in generale, per ogni k positivo,  x → k e^{− k x}, di cui, infatti, l'integrale tra 0 e ∞ è 1  ( ∫ k e^{− k x} dx = −e^{− k x} + c, e per x tendente a ∞, essendo k>0, tende a c, mentre per x che tende a 0 tende a c−1: la differenza è 1).