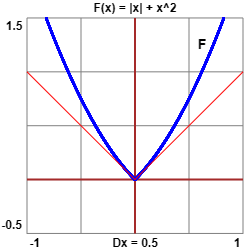
Sia F: x → |x| + x². Sudiare la derivabilità e la concavità di F nel suo dominio.

Sappiamo che x → |x| e che x → x2 sono crescenti in [0,∞) e decrescenti in (−∞,0], quindi sarà tale anche la loro funzione somma. In 0 la funzione x → |x| ha grafico che arriva in (0,0) da destra con pendenza 1 e da sinistra con pendenza −1, mentre la funzione x → x2 vi arriva con pendenza 0. Quindi F ha grafico che arriva in (0,0) come x → |x|, da destra con pendenza 1 e da sinistra con pendenza −1. A destra ne è tracciato il grafico attorno a (0,0). In 0 F non è dunque derivabile, mentre lo è altrove (essendo la somma di due funzioni ivi derivabili). F ha inoltre la concavità verso l'alto (ossia è convessa) in quanto somma di due funzioni, x → x2 e x → |x|, che sono tali.

Richiami:   concavità di una funzione  neGli Oggetti Matematici.