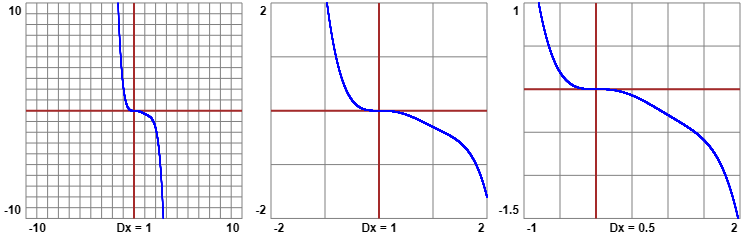
Data la funzione x → −3/10·x⁵ + x⁴ − x³, studiane l'andamento, compresa la concavità, eventualmente trovando alcuni valori (zeri o punti di massimo o minimo o …) in forma approssimata.

Proviamo, prima, a fare tutto graficamente, con l'ausilio del computer. Utilizziamo un semplice script per tracciare grafici, ma si potrebbe usare un qualunque altro buon programma.
Usando questo script per la nostra funzione F ottengo, dopo un po' di prove, una scala ottimale:

A questo punto calcolo F'(x) = -3/2·x4+4·x3-3·x2 e F"(x) = -6·x3+12·x2-6x Modifico lo script aggiungendo il tracciamento di F' e F"   → Ho tutto quello che mi serve per rispondere al quesito.  In (0,0) il grafico ha un punto di flesso con l'asse x come tangente, infatti F' ha ivi un punto di massimo. A conferma, F" ivi si annulla e cambia segno. 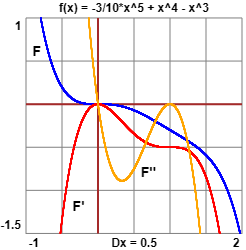F' non è mai positiva, a conferma che F è decrescente. Vi sono infine altri due punti di flesso in quanto non vi sono altri punti, oltre a 0, in cui F" cambi segno.

Ora vediamo come rispondere utilizzando anche i "calcoli".
Si tratta di una funzione polinomale di grado dispari e di coefficiente direttivo negativo, quindi per l'input che tende a ∞ tende a −∞, per l'input che tende a −∞ tende a ∞.  È di grado 5: potrebbe avere da 1 a 5 zeri.  Ma mi rendo conto che, indicato −3/10·x² + x − 1 con H(x), ho F(x) = H(x)·x³.  H(x) < 0 per ogni x, per cui F(x) = 0 solo quando x³ = 0, ossia solo per x = 0.
Studiamo le derivate di F.  F '(x) = −3/2·x⁴+4x³−3x² = (−3/2·x²+4x−3)x²; il primo termine è sempre negativo, per cui tale prodotto si annulla solo per x = 0.  Posso dedurre che per x = 0, in cui F decresce, ho l'unico punto di flesso a tangente orizzontale.
F "(x) = −6x³+12x²−6x = −6(x²−2x+1)x = −6(x−1)²x.  Si azzera per x = 0, dove ho già trovato esservi un flesso discendente, e in x = 1, dove non c'è alcun flesso (F" si mantiene negativa a destra e a sinistra di 1):  si noti che se vi è un flesso ed esiste la derivata seconda, questa deve essere nulla, ma dal fatto che questa sia nulla non si può dedurre che si tratti di un punto di flesso.

Richiami:   concavità di una funzione  neGli Oggetti Matematici.