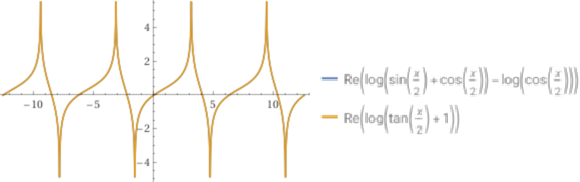
Calcola    ∫ 1 / ( 1+sin(x)+cos(x) ) dx    (procedi per sostituzione)

t = tan(x/2),  sin(x) = 2t/(1+t²),  cos(x) = (1−t²)/(1+t²) (vedi), dt/dx = (1+t²)/2, dx = 2dt/(1+t²)
∫ 1 / ( 1+2t/(1+t²)+(1−t²)/(1+t²) ) 2dt/(1+t²) = ∫ 1/(1+t) dt = log(1+t)
∫ 1 / ( 1+sin(x)+cos(x) ) dx = log( 1 + tan(x/2) )  (+ costanti diverse per ciascun intervallo in cui la funzione è definita).

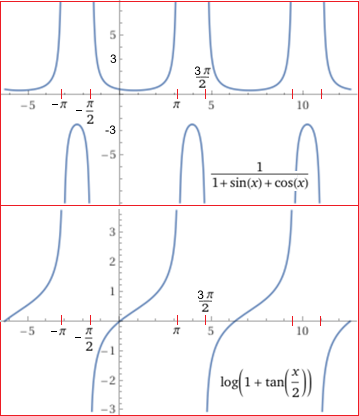
Ma il dominio dell'integranda è tutto R meno un insieme di punti isolati, come si vede nella figura a destra in alto, mentre l'integrale ottenuto sopra non è definito nell'intervallo [π,3π/2] e negli intervalli ottenuti traslando questo di multipli di 2π, come si vede nella figura a destra in basso.     Le figure sono state ottenute con WolframAlpha coi comandi  plot 1 / ( 1+sin(x)+cos(x) ), -2PI < x < 4PI  e  plot log( 1 + tan(x/2) ), -2PI < x < 4PI.     L'errore è stato commesso nel calcolo di ∫ 1/(1+t) dt, che non ha tenuto conto che ∫ 1/x dx, oltre che log(x) (+c), vale anche log(−x) (+c).     Le altre soluzioni sono, dunque, log(−1 − tan(x/2) )  (+ costanti diverse per ciascun intervallo in cui la funzione è definita).     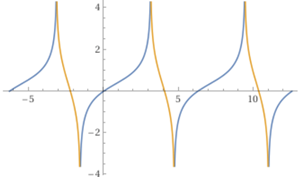Tracciamo con WolframAlpha anche questa funzione: plot log( 1 + tan(x/2) ), plot log(-1-tan(x/2)), -2PI < x < 4PI

Vedi  calcolo di integrali neGli Oggetti Matematici.

    Qualche approfondimento.

    Proviamo a tracciare con WolframAlpha sia il grafico dell'integranda che quello della funzione integrale (lasciando indicato l'operatore di integrazione):

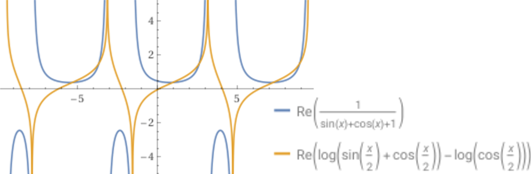
    Nel grafico compare "Re(...)", a indicare la "parte reale", nel senso che la funzione ha anche una componente "complessa", che a noi comunque non interessa.

    L'integrale viene indicato con un'altra formula, che possiamo verficare graficamente essere equiavlente all'altra: