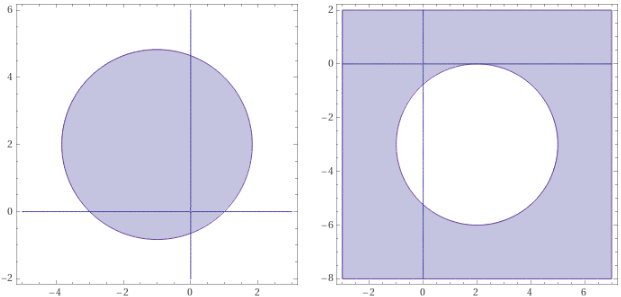
Scrivi due disequazioni che descrivano le figure tracciate sotto  (la parte interna e quella esterna di due differenti cerchi).

La prima figura è l'interno del cerchio centrato in C = (-1,2) e con raggio R che va da (-1,2) a, per esempio, (1,0), ossia R = √(2²+2²) = √8.
È l'insieme dei punti (x,y) tali che √((x+1)²+(y-2)²) < √8, ossia tali che  (x+1)²+(y-2)² < 8.

La seconda è l'esterno del cerchio centrato in (2,-3) con raggio 3:  (x-2)²+(y+3)² > 9.

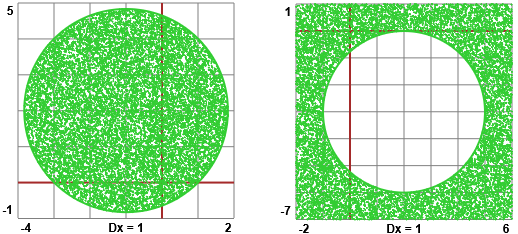
I grafici con questo e questo script.

Come tracciare le figure col software online WolframAlpha (vedi):
(x+1)^2+(y-2)^2 <= 8 and x*y=0, -5 < x < 3, -2 < y < 6
(x-2)^2+(y+3)^2 >= 9 and x*y=0, -3 < x < 7, -8 < y < 2