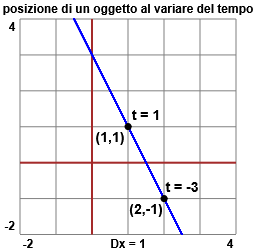
Sia  P(t) = ( x(t), y(t) )  la posizione che un oggetto ha (rispetto a un sistema di coordinate x,y fissato) all'istante t  (espresso in secondi assumendo come riferimento un dato istante fissato).  Sappiamo che l'oggetto si muove lungo una traiettoria rettilinea, che all'istante  t = 1  ha la posizione  P(1) = (1, 1) e che all'istante  t = −3  (ossia 3 secondi prima dell'istante scelto come riferimento)  ha la posizione  P(−3) = (2, −1). 1)  Descrivi la traiettoria dell'oggetto mediante una coppia di equazioni:         x(t) = …         y(t) = … 2)  Descrivila, poi, mediante una equazione del tipo  y = f(x).

In 4 secondi l'oggetto varia la x di −1 e la y di 2.
Quindi, per  Δt = 1,  Δx = −1/4  e  Δy = 1/2.
All'istante t = 0 l'oggetto è dunque in  (1,1) − (−1/4, 1/2) = (5/4, 1/2).
Posso quindi descrivere il moto con  x = 5/4 − t/4,  y = 1/2 + t/2.
Controllo:  per t = 1 ottengo x = 1, y = 1;  per t = −3 ottengo x = 2, y = −1; OK.
Alternativa.  Se l'oggetto fosse in (1,1) all'istante t = 0 il moto sarebbe:
x = 1 − t/4, y = 1 + t/2.  Se traslo il tempo di 1 devo cambiare le equazioni in:
x = 1 − (t−1)/4, y = 1 + (t−1)/2   che, come si vede, equivalgono a quelle trovate nell'altro modo.
Equazione della retta.  Retta per (1,1) con pendenza −2:
y = 1 − 2(x−1).
Controllo: per x = 1 y = 1, per x = 2 y = −1. OK