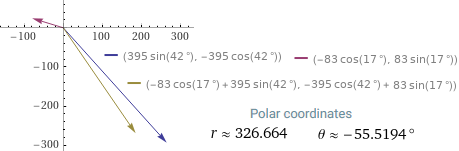[controlla i risultati utilizzando la figura a lato e tracciando su di essa il vettore somma dei due rappresentati]
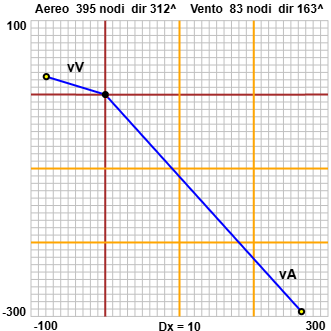
Dalla figura (vedi sotto) possiamo renderci conto che la velocità sarà di circa 330 nodi e diretta circa a -60°.
|
Un aereo vola alla velocità di 395 nodi con direzione 312°. C'è un vento di 83 nodi che soffia con
direzione 163°. Qual è la velocità reale dell'aereo? [controlla i risultati utilizzando la figura a lato e tracciando su di essa il vettore somma dei due rappresentati] |  |
|
Per renderci meglio conto del problema possiamo esprimere le velocità in chilometri all'ora.
Il nodo equivale ad un miglio nautico l'ora, ossia a 1.852 km/h. Quindi l'intensità della velocità dell'aereo
è di 1.852·395 = 731.54 km/h e quella del vento è di 1.852·83 = 153.716 km/h. Dalla figura (vedi sotto) possiamo renderci conto che la velocità sarà di circa 330 nodi e diretta circa a -60°. |
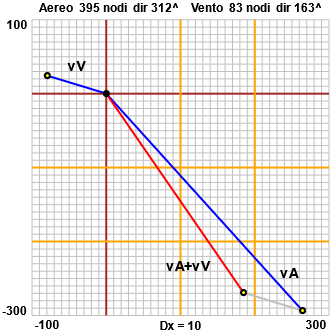 |
Facciamo i conti.
Esprimiamo i vettori (del volo dell'aereo e del vento) esplicitandone le componenti: Lo script online con cui è stato realizzato il grafico. Per altri commenti:
|
Calcoli e grafici col software online WolframAlpha (vedi).
vector(cos(312°)*395,sin(312°)*395), vector(cos(163°)*83,sin(163°)*83), vector(cos(312°)*395+cos(163°)*83, sin(312°)*395+sin(163°)*83)