Determinare l'angolo da formato dai vettori u = (1, −2, 2) e v = (−4, 0, 2).

Usando la definizione di "·" che ricorre alle componenti dei vettori ho: u·v = 1(−4)+(−2)0 + 2·2 = 0. Usando quella che usa l'angolo θ formato da essi ho: ||u|| = 3, ||v|| = 2√5, u·v = 6√5 cos(θ). Quindi cos(θ) = 0, ossia i due vettori devono essere tra loro perpendicolari. A lato l'illustrazione dei due vettori.

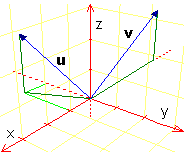
(clicca l'immagine per ingrandirla)

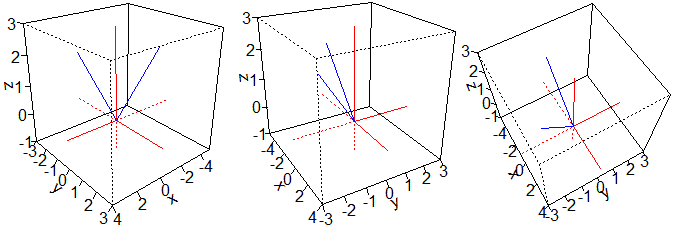
Per altri commenti: lo spazio tridimensionale neGli Oggetti Matematici.

lo spazio x da -5 a 4, y da -3 a 3, z da -1 a 3
da tre punti di vista diversi: