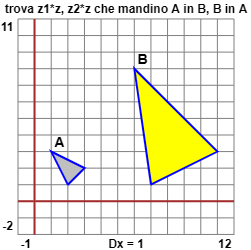
Determina le funzioni (C → C)  z → z1·z  e  z → z2·z  che, rispettivamente, trasformano il triangolo piccolo in quello grosso e viceversa.
(la figura è stata realizzata con questo script)

In entrambi i casi si tratta di una composizione di una trasformazione di scala monometrica (omotetia) di fattore pari al modulo del numero per cui z viene moltiplicato e di una rotazione di ampiezza pari all'argomento del numero stesso. Per trovare questo numero basta imporre che la moltiplicazione per esso associ a un punto il suo trasformato.

Per trovare z₁ osservo che (2,1) viene trasformato in (7,1), ovvero che z₁·(2+i) = 7+i. Scrivo z₁ come x₁+iy₁. Devo imporre che:

(x₁+iy₁)(2+i) = 7+i
2x₁-y₁+ (2y₁+x₁)i = 7+i
2x₁-y₁ = 7 AND 2y₁+x₁ = 1
4x₁-2y₁ = 14 AND 2y₁+x₁ = 1
5x₁ = 15 AND 2y₁+x₁ = 1
x₁ = 3 AND 2y₁+3 = 1
x₁ = 3 AND y₁ = -1     z₁ = 3-i
z₂ è il reciproco di z₁. Posso trovarlo in vari modi. In questo caso è semplice fare:
z₂ = 1/(3 - i) = (3 + i)/( (3 - i)(3 + i) ) = (3 + i)/(3²+i²) = 3/10 + i/10

Verifica con WolframAlpha:
2x1-y1 = 7 AND 2y1+x1 = 1   →   x1 = 3, y1 = -1
1/(3-i)   →   0.3 + 0.1 i