In un ospedale si stabilisce, in base ai sintomi e alle statistiche di cui si dispone, che un particolare paziente può essere affetto dalle malattie A, B e C con le seguenti probabilità: Pr(A)=0.3, Pr(B)=0.2, Pr(C)=0.5. Da un successivo test clinico del paziente si ottiene esito positivo. Sappiamo che mediamente questo test dà esito positivo nel 25% dei casi in cui il paziente ha la malattia A, nel 15% di quelli in cui ha la malattia B e nel 98% di quelli in cui ha la malattia C. Che cosa si può concludere?

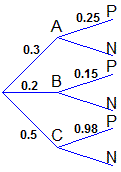
Facendo riferimento al grafo a lato è facile impostare i calcoli seguenti e ottenere che la probabilità di avere la malattia C, Pr(C|P) = 82%, è particolarmente alta, maggiore del 50% che si poteva ipotizzare a priori. Nei calcoli seguenti T è la probabilità di avere esito positivo; vengono confrontate Pr(A|P), Pr(B|P), Pr(C|P). T = 0.3*0.25 + 0.2*0.15 + 0.5*0.98 = 0.595 = 5.95% Pr(A|P)·100 = 0.3*0.25/T*100 = 0.3*0.25/(0.3*0.25 + 0.2*0.15 + 0.5*0.98)*100 = 12.6050420168 Pr(B|P)·100 = 0.2*0.15/T*100 = 0.2*0.15/(0.3*0.25 + 0.2*0.15 + 0.5*0.98)*100 = 5.0420168067 Pr(C|P)·100 = 0.5*0.98/T*100 = 0.5*0.98/(0.3*0.25 + 0.2*0.15 + 0.5*0.98)*100 = 82.3529411765

Per altri commenti: dipendenza e indipendenza neGli Oggetti Matematici.