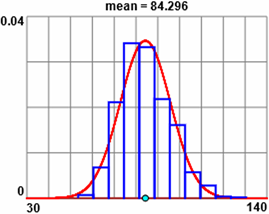
Un'indagine sul peso dei maschi tra i 45 e i 55 anni di un certo stato dà i seguenti esiti grafici rappresentati a lato e quelli numerici riportati qui sotto: median=85 − 1º,3º quartile: 78 92 − mean=84.296 − experim. standard dev. = 11.512 All'istogramma (costituito da 11 colonne) è stato sovrapposto il grafico della gaussiana (di media 84.296 e sigma 11.512).  Utilizzando i dati sperimentali e quelli ottenuti integrando la gaussiana negli intervallini considerati nell'istogramma si è ottenuto 27.1 come chi quadro. (1) Perché i gradi di libertà sono 8? (2) È da accettare l'ipotesi che la distribuzione sia gaussiana?

(1)  Gli intervalli sono 11 e vi sono 3 vincoli:  a) la somma delle frequenze relative è 1,  b) la media e c) la varianza sono date.  Dunque i gradi di libertà sono 11-3 = 8.
(2)  Sembra che vi sia una buona sovrapposizione tra la gaussiana e l'istogramma, ma è una valutazione superficiale:

d.f.     5       10      25      50      75      90      95 
 8       2.73    3.49    5.07    7.34    10.2    13.4    15.5

Il valore 27.1 è ben oltre il percentile di ordine 95 (15.5):  l'ipotesi deve essere decisamente rigettata.