Nelle classi I, II e III di una sezione i maschi e le femmine sono così divisi:

	maschi	femmine	totale
I	14	11	25
II	15	8	23
III	10	10	20

In quale classe ci sono più maschi rispetto al totale?

Devo capire se 14 rispetto a 25 è di più che 15 rispetto a 23 o …. Posso precedere in vari modi. Vediamoli.

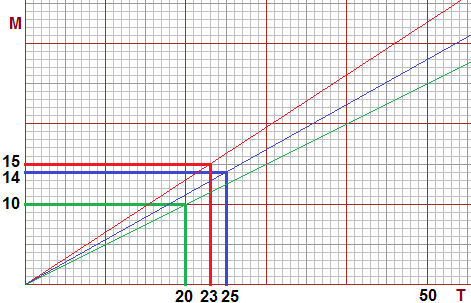
1)  Posso usare una rappresentazione su carta quadrettata o millimetrata come fatto qui sotto:

Vedo che 15 rispetto a 23 (colore rosso, classe II) vale di più che 14 rispetto a 25 (blu, classe I) e che 10 rispetto a 20 (verde, classe III). Infatti quanto pił sono i maschi (M) rispetto al totale della classe (T) tanto più aumenta la pendenza di una di queste rette.
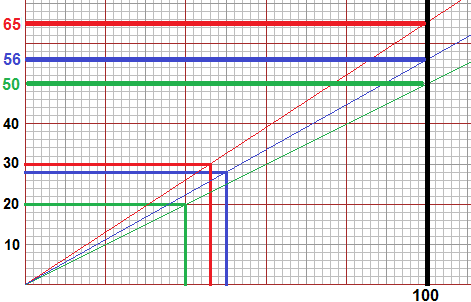
Volendo, osservando i grafici (prolungandoli, o cambiando la scala, come nella figura sotto), vedo che nella classe II se gli alunni fossero 100 e i maschi fossero presenti allo stesso modo, essi sarebbero 65, ovvero 65 maschi su 100 alunni, ovvero il 65 per 100, ovvero, in simboli, il 65%; nella classe I sarebbero il 56%; nella III il 50%.

2)  Posso, tuttavia, procedere senza tracciare i grafici. Ad esempio per valutare che parte di 23 è 15 posso fare la divisione 15/23. Trovo (a mano o con la calcolatrice) 0.652173…; ricordo che questo numero viene chiamato rapporto tra 15 e 23; lo arrotondo a 0.65, ovvero lo esprimo come 65 centesimi, ovvero come 65/100.
Ritrovo il valore trovato sopra. Analogamente trovo 56/100 e 50/100 per i maschi delle altre due classi.
Ricordo che la scrittura 65% è una abbreviazione di 65/100 e che, invece che "65 su 100", si legge in genere "65 per 100", nel senso che "per ogni 100 ce ne sono 65", non col significato che "per" assume per indicare le moltiplicazioni.