| Per studiare gli effetti di un certo virus, in uno studio scientifico 70 cavie sono state infettate con esso e si sono rilevati i loro giorni di sopravvivenza. I dati sono riportati a lato. Come potresti rappresentare queste informazioni in un modo più velocemente e più facilmente comprensibile? | 40, 45, 53, 56, 56, 57, 58, 62, 64, 73, 74, 78, 79, 80, 81, 81, 81, 82, 83, 83, 84, 85, 89, 90, 91, 92, 92, 97, 99, 99, 99, 99,101,102,102,102,103,104,107,108,109,113, 114,118,121,123,126,128,137,138,134,144,145,147,156,162, 174,174,179,184,191,198,208,214,247,249,328,383,403,511 |
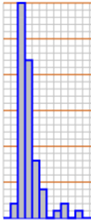
40, 45, 53, 56, 56, 57, 58, 62, 64, 73, 74, 78, 79, 80, 81, 81, 81, 82, 83, 83, 84, 85, 89, 90, 91, 92, 92, 97, 99, 99, 99, 99,101,102,102,102,103,104,107,108,109,113, 114,118,121,123,126,128,137,138,134,144,145,147,156,162, 174,174,179,184,191,198,208,214,247,249,328,383,403,511 | Un modo semplice e breve è quello di prendere come rappresentante dei dati (che sono già in ordine di grandezza) quello che sta, più o meno, a metà, ossia 102, e, per avere un'idea di come sono distribuiti i dati, prendere da una parte quello che sta, circa, a metà della prima metà, ossia 81, e dall'altra quello che sta a metà della seconda metà, ossia 144. Quindi possiamo dire che i dati sono attorno a 102, e che il 50% di essi sta tra 81 e 144. Ricordiamo che il dato che sta a metà dell'elenco ordinato dei dati si chiama mediana. |
Volendo fare un calcolo complicato si potrebbe fare la media dei dati, ottenendo 129.6, ma si tratta di una informazione poco significativa: è distante dal valore centrale (102) in quanto i dati maggiori di quello che sta a metà si disperdono maggiormente di quelli minori.
Riportando i dati in ordine, raggruppati in classi ampie 50 giorni, possiamo capire meglio come sono distribuiti i dati:
|40, 45, |53, 56, 56, 57, 58, 62, 64, 73, 74, 78, 79, 80, 81, 81, 81, 82, 83, 83, 84, 85, 89, 90, 91, 92, 92, 97, 99, 99, 99, 99 101,102,102,102,103,104,107,108,109,113,114,118,121,123,126,128,137,138,134,144,145,147, 156,162,174,174,179,184,191,198, 208,214,247,249, | 328, 383,403, | 511
Potrei anche rappresentare gli stessi dati su carta quadrettata, ottenendo un istogramma simile a quello raffigurato qui a destra. Questa è decisamente la rappresentazione migliore, più facilmente comprensibile. |
 |
L'istogramma a quadretti rappresentato qui a sinistra è stato ottenuto con questo script.
dati = [2,30,22,8,4,0,1,2,0,1] N = 30 G = [5,10,15,20,25,30] titolo="" |
C'è una rappresentazione alternativa agli istogrammi, su cui si tornerà negli studi successivi: invece di figure in due dimensioni figure in una dimensione. Sono i box-plot, diagrammi dalla forma di "scatola", in cui la parte centrale rappresenta il 50% centrale dei dati, suddivisa in due parti da una tacca che rappresenta la mediana. Ecco che cosa si può ottenere con lo script "box-plot":
È anche questa una rappresentazione che illustra efficacemente e in modo comprensibile la distribuzione dei dati, occupando poco spazio.