Da un tavola antropometrica rileviamo le informazioni riportate nella tabella seguente, relative a uno studio realizzato su un ampio campione di popolazione europea negli anni sessanta.  (1) Associa a ciascuna grandezza (i cui valori sono espressi in cm) il corrispondente box-plot.  (2) Valuta la probabilità che un bambino europeo di 3 anni a quell'epoca fosse alto più di 1 metro.		94% delle misure 3 anni maschi   80% delle misure     50% delle misure   3° 10° 25° 50° 75° 90° 97°  ordine del percentile 90.6 92.3 93.9 96.2 98.5 100.5 102.8 altezza 48.9 49.9 51.0 52.4 54.1 55.8 57.9 circonf. toracica

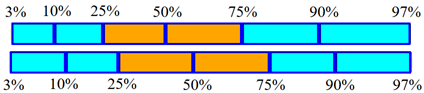(1)  Il box-plot in basso è più "simmetrico" di quello in alto.  La riga più simmetrica rispetto alla mediana è quella delle altezze, infatti gli intervalli tra 25° e 50° percentile e quello tra 50° e 75° sono ampi entrambi 2.3; in quella delle altezze gli stessi intervalli sono abbastanza diversi tra loro: uno è ampio 1.4, l'altro 1.7.  Il box-plot in basso dovrebbe quindi essere associato alla altezza e quello in alto alla circonferenza toracica.

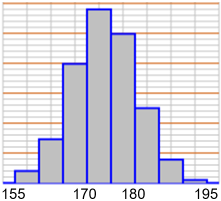
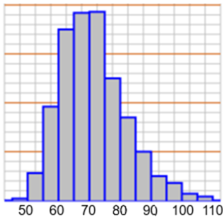
Del resto è noto che le altezze si distribuiscono in modo rappresentabile con un istogramma simmetrico dalla forma a campana (istogramma sotto a sinistra). La stessa cosa non accade per il peso (istogramma sotto a destra) e, come ora abbiamo visto, per la circonferenza toracica. Vedi gli esercizi 3 e 5 in fondo alla voce "distribuzione".

(2)  100 cm sta tra il 75° percentile (98.5 cm) e il 90° (100.5 cm). Per stimare il perecentile corrispondente osserviamo che variando l'ordine del percentile di 15 (dal 75º al 90º) il valore varia di 2 cm; facendo una valutazione proporzionale possiamo stimare che 0.5 cm (che da 100 cm portano a 100.5 cm) corrisponda a una variazione di 1/4 di 15, ossia 4: il percentile corrispondente è circa 86, e la probabilità richiesta è 100%-86% = 14%.