Utilizzando in modo opportuno il teorema del coseno (o di Carnot) o il teorema del seno (o della corda), dato il triangolo ABC:
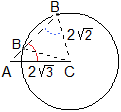
(a) in un caso, noti  BC = 2√2, AC = 2√3, sapendo che l'angolo in A è di 45°, determinare gli altri angoli;
(b) nell'altro, noti  AB = 14, BC = 10 e AC = 6, determinare gli angoli.

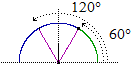
Per i riferimenti ai due teoremi si veda Funzioni circolari e trigonometria neGli Oggetti Matematici.     Nel primo caso posso usare il teorema del seno. Indicando con α, β e γ le ampiezze degli angoli in A, B e C, ho: sin(β) = sin(α)/BC·CA = √2/2 / (2√2)·2√3 = √3/2   da cui β = 60° o β = 120°. γ sarà in un caso di (180-45-60)° = 75°, nell'altro di (180-45-120)° = 15°.

    Nel secondo caso posso usare il teorema di Carnot:
cos(α) = (6²+10²−14²)/(2·6·10) = −60/120 = −1/2, da cui α = 120°.
cos(β) = (14²+10²−6²)/(2·14·10) = 13/14, da cui α = acos(13/14) = 21.7867892982618...°
cos(γ) = (14²+6²−10²)/(2·14·6) = 11/14, da cui α = acos(11/14) = 38.213210701738...°
Controllo (con "calcolatrice2" presente QUI):  (acos(13/14)+acos(11/14))*180/PI = 60.  OK.

In entrambi i casi posso trovare le soluzioni usando gli script "tri lato-lato-ang" e "tri lato-lato-lato" presenti QUI:
(a)




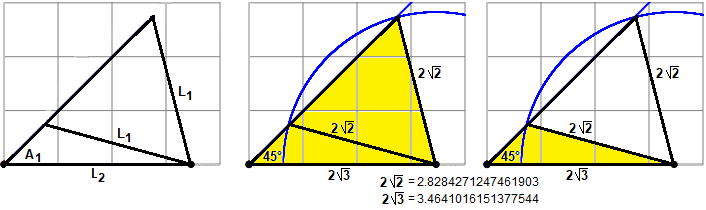
(b)