Il test χ²

In questa voce ci occuperemo di alcune (tra le molte) tecniche per prendere delle decisoni sulla base di dati statistici raccolti sperimentalmente.

  Verifica della verosimiglianza delle ipotesi

    Valutata la probabilità di un evento o individuata una legge di distribuzione o … solo sulla base di dati sperimentali, non abbiamo la certezza di questa conclusione. Possiamo, comunque, porci il problema di quanto sia verosimile l'ipotesi che il valore o la funzione o … individuata sia effettivamente una buona approssimazione, cioè valutare la probabilità che il suo scarto dall'oggetto (valore, funzione, …) "vero" rientri nei margini di aleatorietà dovuta alla limitatezza del materiale statistico a disposizione. In base a questa valutazione, a seconda della situazione (con considerazioni pratiche, legate al contesto, ai rischi sociali, …), potremo stabilire se tale ipotesi è accettabile o è da rifiutare.

    Abbiamo affrontato attività di questo tipo alla voce limiti in probabilità:  all'intervallo frequenza ± 3 σ/√n associo la probabilità di confidenza del 99.7% che esso contenga la probabilità Pr(A) cercata; all'intervallo frequenza ± t σ/√n con t<3 posso associare una probabilità di confidenza più piccola; in altre parole valuto ( la probabilità che tale l'intervallo sia veramente un intervallo di indeterminazione per Pr(A).

    Se in base a qualche ragionamento ho ipotizzato che Pr(A) sia 3/7 e trovo che 3/7 sta nell'intervallo frequenza ± t σ/√n, posso ritenere attendibile (con una opportuna confidenza) che lo scarto tra 3/7 e frequenza sia "normale", cioè ritenerlo non "significativo", non tale da giustificare il rifiuto dell'ipotesi. Questa terminologia (accettazione/rifiuto dell'ipotesi) in realtà non è fondata: la probabilità dell'ipotesi che Pr(A) sia "esattamente" 3/7 è nulla. Ma è un modo di esprimersi "convenzionale" ormai diffuso.

    In questa voce vedremo in particolare come valutare l'attendibilità di una legge di distribuzione.

  Verifica della verosimiglianza di una legge di distribuzione. Il test "chi quadro".

    Poniamoci il problema di valutare la conformità tra una distribuzione sperimentale e una teorica.

    Per valutare la discordanza tra un valore sperimentale U_s e un valore teorico U uso la differenza (o errore o scarto o deviazione) U_s–U.

    Come valutare la discordanza tra gli esiti di n prove, classificati in nc classi, e una certa legge di distribuzione?

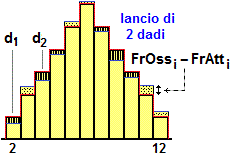
    Supponiamo di voler confrontare con la distribuzione Pr(U=2)=1/36, Pr(U=3)=2/36, … gli esiti del lancio di una coppia di dadi ripetuto n volte. Indichiamo con FrOs₁, …, FrOs₁₁ le frequenze assolute osservate (FrOs₁ + FrOs₁₁= n) e con FrAt₁, …, FrAt₁₁ le frequenze assolute attese, cioè i valori che si otterrebbero da  FrequenzaAssoluta = n · FrequenzaRelativa  mettendo  Probabilità al posto di  FrequenzaRelativa:  FrAt₁ = n·1/36, FrAt₂ = n·2/36, ….

Un'idea è prendere   X = Σ(FrOsi−FrAti)2 / FrAti   infatti: •  l'elevamento al quadrato fa sì che differenze positive (zone punteggiate nella figura a lato) e quelle negative (zone tratteggiate) non si compensino; •  la divisione per le frequenze attese fa sì che una differenza come d1 (nella figura a lato) pesi di più di una come d2, che sarebbe leggermente maggiore ma relativa a dati molto più piccoli (la deformazione dall'istogramma teorico è maggiore se si è in un punto in cui il grafico è basso).     Tale valore viene indicato con χ2  ("chi quadro"):

χ2 =  nc Σ i=1 (FrOsi − FrAti)2 ——————— FrAti

    Lo stesso valore viene preso nel caso di un'altra variabile casuale.  Cambia il modo in cui sono calcolate le frequenze attese nelle nc classi (intervallini o altri insiemi) I_i in cui ho classificato gli n dati;  se la variabile casuale è continua sono calcolate integrando su I_i la funzione densità.

    χ² è una variabile aleatoria (assume un valore diverso ogni volta che effettuo n prove) che, oltre che dal fenomeno studiato, dipende dal numero delle prove n,  dalle classi  I₁, …, I_nc  scelte  e  dalla legge di distribuzione teorica L di cui si vuole valutare la verosimiglianza, da cui dipendono le frequenze attese.

    Consideriamo ad esempio un dado di cui si sono effettuati 50 lanci ottenendo 9 uno, 11 due, 5 tre, 8 quattro, 10 cinque e 7 sei.  Per valutare la discordanza dalla distribuzione uniforme (distribuzione corrispondente ai dadi equi), calcoliamo il relativo χ².  Poniamoci, poi, il problema di individuare la distribuzione χ² teorica nel caso in cui il dado sia realmente equo, in modo da poter confrontare con essa il χ² trovato e valutare la verosimiglianza dell'equità del nostro dado.

    Potremmo svolgere il calcolo "a mano".  Effettuiamolo mediante lo script "test χ²" presente qui.  Otteniamo 2.8.

    Effettuato questo calcolo, che cosa possiamo concludere sulla equità del dado?
    Studiamo la distribuzione teorica χ², cioè come si distribuirebbe il valore di χ² se il dado fosse equo.  Realizziamo questo studio sperimentalmente, con una simulazione dei 50 lanci. Ecco l'esito della generazione di 7800 valori generati con un programmino in JavaScript e analizzati con lo script "istogramma". Vedi qui se vuoi vedere come generare i dati e analizzarli.

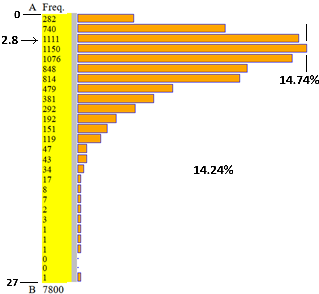A = 0,   B = 27,   27 intervalli di ampiezza 1 n = 7800,   min = 0,   max = 26 mediana = 4,   1º | 3º quartile = 2 | 6 media = 4.6570512820513 percentuali: 3.62 | 9.49 | 14.24 | 14.74 | 13.79 | 10.87 | 10.44 | 6.14 | 4.88 | 3.74 | 2.46 | 1.94 | 1.53 | 0.6 | 0.55 | 0.44 | 0.22 | 0.1 | 0.09 | 0.03 | 0.04 | 0.01 | 0.01 | 0.01 | 0 | 0 | 0.01 |

    Posso osservare dall'istogramma che 2.8 è un valore abbastanza centrale rispetto alla distribuzione dei dati. Esaminando le uscite osservo che 2.8 sta tra il 25º percentile (o primo quartile, 2) e la mediana (4), e quindi sta nel 50% centrale dei dati.
    Quindi posso ritenere plausibile (cioè non rifiutare) l'ipotesi che il dado sia equo.  Se avessi ottenuto un valore verso la coda sinistra o quella destra avrei invece dovuto avere dubbi su tale ipotesi: se è verso la coda destra si tratta di un valore molto alto, che fa supporre un dado non equo; se è verso la coda sinistra si tratta di un valore molto basso, ma un po' troppo "perfetto", che fa supporre che ci sia stato qualche errore (o qualche "imbroglio") nel riportare le frequenze.  In tali casi, prima di scartare l'ipotesi, sarebbe stato opportuno, se possibile, ripetere i lanci, ricalcolare χ² e valutare la posizione del nuovo valore rispetto all'istogramma sopra riprodotto (o rispetto ai percentili).

    Nel caso di un'altra legge di distribuzione L, altre classi o un altro numero n di prove, si può procedere analogamente: studiare sperimentalmente con una simulazione la distribuzione del relativo χ² e confrontare con essa il valore calcolato di χ².  In genere, tuttavia, si preferisce utilizzare un procedimento standard di tipo generale, che ha il seguente retroterra teorico:

si può dimostrare che, se il numero n delle prove è sufficientemente grande, la legge di distribuzione teorica di χ² è praticamente indipendente dalla legge di distribuzione L:

per n tendente all'infinito tende a una legge χ²(r) che dipende solo dal numero r dei gradi di libertà, cioè dalla quantità delle frequenze sperimentali che devo conoscere direttamente.

    Spieghiamo meglio il concetto di "grado di libertà"  (nello script precedente compariva denominato in inglese, "degrees of freedom")  con alcuni esempi.

    Nel caso del dado sopra considerato, sappiamo che le frequenze FrOs₁, FrOs₂, …, FrOs₆ devono avere come somma n.  Questa connessione fa sì che note 5 frequenze la rimanente sia determinata automaticamente.  Tale connessione è presente in tutti i casi.  Quindi i gradi di libertà sono in ogni caso al più  nc−1  (nc = numero delle classi).

    Nel caso di una variabile casuale a valori reali positivi, se FrOs₁,…, FrOs₁₆ sono le frequenze osservate nei 16 intervalli [0,5), [5,10), … e voglio operare il confronto con la densità esponenziale  x → w·exp(−w·x)  con w pari al reciproco della media sperimentale M, come connessione imposta, ulteriore rispetto a  ΣFrOs_i = n, ho che  Σx_i·FrOs_i / n = M  (x_i centro dell'intervallo i-esimo: x₁=2.5, x₂=7.5, …).  I gradi di libertà sono 16−2 = 14.  Note 14 tra le FrOs_i, ad es. FrOs₁, FrOs₂, …, FrOs₁₄, potrei determinare FrOs₁₅ e FrOs₁₆ risolvendo il sistema (avente FrOs₁₅ e FrOs₁₆ come incognite):   ΣFrOs_i = n  AND  Σx_i·FrOs_i/n = M.

    Se, invece, come w avessi scelto un valore stabilito a priori, non dipendente dai dati sperimentali, non avrei avuto la connessione Σx_i·FrOs_i /n = M, e i gradi di libertà sarebbero stati 15.

    L'espressione di χ²(r) non è facile da descrivere né da comprendere (non è una delle cosiddette funzioni "elementari": vedi).  Comunque nel software matematico in genere è definita e richiamabile con degli opportuni comandi.  Ecco, sotto, a sinistra, il grafico della densità di χ²(5) corrispondente all'istogramma ottenuto sopra per il dado equo, e, a destra, i grafici delle densità per i gradi di libertà inferiori tratti da WolframAlpha:

df = 5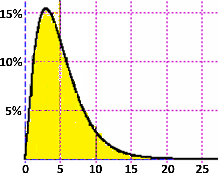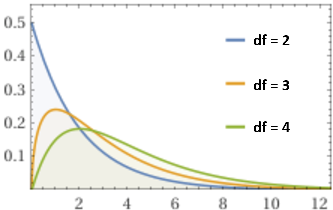

    Ecco, qua sotto, arrotondati, i valori del 5º, del 10º, …, del 95º percentile per diversi gradi di libertà, una parte di quelli che appaiono elencati azionando lo script test χ²:

d.f.     5       10      25      50      75      90      95 
 1       0.00393 0.0158  0.102   0.455   1.32    2.71    3.84
 2       0.103   0.211   0.575   1.39    2.77    4.61    5.99
 3       0.352   0.584   1.21    2.37    4.11    6.25    7.81
 4       0.711   1.06    1.92    3.36    5.39    7.78    9.49
 5       1.15    1.61    2.67    4.35    6.63    9.24    11.1
 6       1.64    2.20    3.45    5.35    7.84    10.6    12.6
 8       2.73    3.49    5.07    7.34    10.2    13.4    15.5
 9       3.33    4.17    5.90    8.34    11.4    14.7    16.9
 10      3.94    4.87    6.74    9.34    12.5    16.0    18.3
 15      7.26    8.55    11.0    14.3    18.2    22.3    25.0
 20      10.9    12.4    15.5    19.3    23.8    28.4    31.4
 30      18.5    20.6    24.5    29.3    34.8    40.3    43.8
 50      34.8    37.7    42.9    49.3    56.3    63.2    67.5
 75      56.1    59.8    66.4    74.3    82.9    91.1    96.2
 100     77.9    82.4    90.1    99.3    109     118     124

    Tornando al nostro dado (5 gradi di libertà), se come χ² invece di 2.8 (che è intorno al 25º percentile e quindi è abbastanza "normale") avessimo ottenuto 13 avremmo dovuto manifestare qualche dubbio sul fatto che il dado sia equo: c'è una discordanza molto alta rispetto alla legge uniforme: il 95º percentile è 11.1.

    Ma anche se avessimo ottenuto una discordanza molto bassa, ad esempio χ²<1, avremmo dovuto avere dei dubbi sulla equità del dado o sulla attendibilità dei dati fornitici:  è improbabile che si ottenga un valore inferiore a 1  (la probabilità è inferiore al 5%: il 5º percentile è 1.15).

    Altro esempio. Se un amico mi dice:  Questa moneta è equa. Infatti su 1000 lanci ho ottenuto 499 "testa" e 501 "croce".  Che cosa posso concludere sulla verosimiglianza di quanto raccontato dall'amico?

Trovo χ² = (499–500)²/500+(501−500)²/500 = 2/500 = 4/1000  (ovvero metto nello script "Test χ²"  O: 499, 101  e  E: 1,1;  ottengo 0.004).

I gradi di libertà sono 2-1 = 1. Dalla tabulazione ho che 0.004 corrisponde circa al percentile di ordine 5. Si tratta quindi di un valore piuttosto anormale. È sensato ritenere che l'amico ci abbia raccontato una frottola.

    Nell'usare la distribuzione del χ² limite occorre prestare qualche attenzione: occorre che le prove siano numerose (diciamo, almeno un centinaio); occorre, inoltre, che in ogni classe (di quelle in cui le prove sono state classificate - da chi ha fornito le informazioni o direttamente da voi) cadano abbastanza valori (diciamo, almeno 5); se in qualche classe cadono poche osservazioni è opportuno unire questa classe ad un'altra.

Esercizio 1   soluzione         Esercizio 2   soluzione         Esercizio 3   soluzione

  Altri test di significatività

    Abbiamo dato un'idea del significato e di alcuni impieghi del test χ².  Esitono vari altri tipi di test.
    Puoi trovare qualche approfondimento in WolframAlpha  (vedi)  e in Wikipedia, versione inglese  (ad esempio: Test statistic,  Chi-squared test,  Statistical hypothesis test,  Student's t-distribution,  Kolmogorov-Smirnov test).