I numeri complessi

  Introduzione

Se in WolframAlpha inserisco il comando: solve 7*x^4 + sqrt(3)*x^3- x^2 + 2*x + 2/3 = 0 for x real ottengo:   x ≈ -0.732581   x ≈ 0.294221     Se invece inserisco: solve 7*x^4 + sqrt(3)*x^3- x^2 + 2*x + 2/3 = 0 for x ottengo:  x ≈ -0.732581,  x ≈ 0.294221,  x ≈ 0.38968 - 0.53852 i  x ≈ 0.38968 + 0.53852 i ossia 2 altre soluzioni.    Che cosa sono questi 2 altri "numeri", 0.38968 - 0.53852 i  e  0.38968 + 0.53852 i?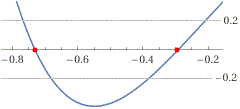

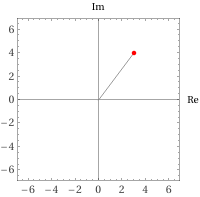
Sappiamo che non sono "real".     Proviamo a inserire  3 + 4i  e poi  3 + 0i.  In un caso ottengo la visualizzazione a lato.  Nell'altro ottengo il "risultato" 3.  Che cosa posso concludere?     Pare che  3+0i  sia un modo alternativo per rappresentare il numero reale 3.  Sembra, inoltre, che il numero  3+4i  sia un modo per rappresentare il punto di coordinate (3,4).     Ma che cos' questo i che compare?  Che ruolo ha in matematica?     In questa voce daremo una risposta a queste domande.     Ad un primo livello ci si pu fermare alle prime due sezioni ("Dai vettori ai numeri complessi", "Le operazioni tra numeri complessi").  Gli altri paragrafi sono da intendere come approfondimenti affrontabili, in alcuni tipi di scuola, o, eventualmente, alla fine delle superiori.

  Dai vettori ai numeri complessi

    Alla voce vettori abbiamo introdotto l'uso delle coppie di numeri per descrivere traslazioni, dopo che le avevamo già impiegate per descrivere punti dello spazio bidimensionale (piano cartesiano). Abbiamo introdotto anche una operazione di addizione tra tali coppie, per rappresentare la composizione di due traslazioni. Abbiamo poi introdotto la differenza tra coppie di numeri:  le figure seguenti ricordano come la differenza  (4,1) – (1,3) = (4-1, 1-3) = (3, -2) che rappresenta il vettore AB può essere interpretata sia come differenza tra i punti B e A, sia come differenza tra i vettori OB e OA (il vettore AB è quanto devo aggiungere al vettore OA per ottenere il vettore OB).

    La traslazione di una figura con passi Δx = 3, Δy = -2 può essere descritta come la applicazione della funzione  (x,y) → (x,y) + (3,-2) = (x+3, y-2)  a tutti i suoi punti.  Alla voce trasformazioni geometriche abbiamo visto come descrivere analogamente alcune particolari rotazioni attorno all'origine:
– il pesce della figura (A) seguente diventa il pesce di (B) mediante una rotazione di 90° (π/2) descrivibile come (x,y) → (-y, x)
– il pesce (A) diventa il pesce (C) mediante una rotazione di 180° (π) descrivibile come (x,y) → (-x,-y)
– il pesce (A) diventa il pesce (D) mediante una rotazione di 270° (3π/2), o -90°, descrivibile come (x,y) → (y,-x)

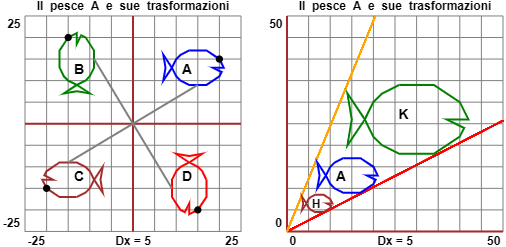
    Abbiamo anche visto anche come realizzare simmetrie rispetto all'asse x e all'asse y e trasformazioni di scala, come quelle raffigurate sopra a destra:  il pesce H è stato ottenuto una trasformazione di scala monometrica (od omotetia di centro O) di fattore 1/2 descrivibile come (x,y) → (x, y)/2 = (x/2,y/2) (moltiplicazione di (x,y) per il numero reale 1/2: direzioni e funz. circolari), il pesce K con una di fattore 2.

(le figure precedenti sono state tracciate con questo e questo script)

    Per semplificare la descrizione sia dei punti che delle trasformazioni geometriche (evitando l'uso delle parentesi e delle virgole) e, come vedremo, per trovare un modo semplice per descrivere anche le rotazioni di ampiezza diversa rispetto ai multipli di 90°, si introduce il seguente "trucco", che descriviamo riferendoci alla figura sotto a destra:

– posso pensare il punto P = (3,2), cioè il vettore OP, come somma del vettore (3,0) (il vettore di modulo 3 diretto come l'asse x) e del vettore (0,2) (di modulo 2 diretto come l'asse y):  (3,2) = (3,0) + (0,2). – abbreviando, scrivo 3 al posto di (3,0) e, indicando con i il versore verticale, cioè il vettore (0,1), scrivo 2i al posto di (0,2); posso dunque scrivere:  (3,2) = 3 + 2i.     In pratica descrivo la coppia come se fosse un termine numerico dato dalla somma di un numero reale (3) e il prodotto (2i) di un numero per il simbolo di costante i, che posso pensare come l'unità di misura degli spostamenti sull'asse verticale.

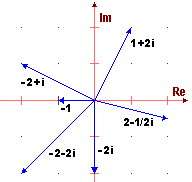i, in quanto simbolo di costante "inventato", che non corrisponde a un usuale numero, viene chiamato unità immaginaria, e le espressioni del tipo  x + iy,  somma di un numero reale e di un numero reale "moltiplicato per i", vengono dette numeri complessi.     L'espressione "numeri reali" è stata introdotta dopo l'invenzione dell'uso di i, per precisare che si tratta di numeri usuali in cui non compare l'unità immaginaria.     Quando si usano rappresentazioni grafiche come quelle illustrate sopra e a sinistra, gli assi delle ascisse e delle ordinate vengono chiamati anche asse reale e asse immaginario. E, dato il numero complesso, x + iy, a cui corrisponde il punto (x,y), x viene detta sua parte reale e y sua parte immaginaria.  In simboli:  x = Re(x + iy), y = Im(x + iy).

    Sopra sono rappresentati vari numeri complessi. Tra questi vi è anche un numero con parte reale nulla (-2i, rappresentato da un vettore verticale) e uno con parte immaginaria nulla (-1, rappresentato da un vettore orizzontale), ossia un numero complesso che è anche un numero reale.  Con le convenzioni usuali, -2-2i sta per -2+(-2)i, ossia ha -2 come parte immaginaria.

  Le operazioni tra numeri complessi

    L'insieme dei numeri complessi viene indicato con 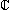o con C. Ad esso si possono estendere l'addizione e la moltiplicazione di R in modo che si mantengano le proprietà illustrate alla voce termini equivalenti.
    L'addizione non è altro che quella tra vettori: (4 + 6 i) + (2 + 3 i) diventa la somma dei vettori rappresentati da 4, da 6i, da 2 e da 3i, che posso riordinare come voglio, per cui posso ottenere:

(4 + 6 i) + (2 + 3 i) = 4+2 + (6i+3i) = 6 + 9i.

    Nel trasformare 6i+3i in 9i ho fatto:  6 i + 3 i = 6(0,1) + 3(0,1) = (0,6) + (0,3) = (0+0,6+3) = (0,9) = 9 i.

    Effettuando la moltiplicazione tra due generici numeri complessi in modo che valga la proprietà distributiva abbiamo, ad es.:

(7 + 10 i) · (4 + 3 i)  =  7·4 + 10·4 i + 7·3 i + 10·3 i·i  =  28 + 61 i + 30 i·i.

    Per completare il calcolo trasformando il risultato in una espressione del tipo x+iy dobbiamo stabilire quanto fa i·i.

L'addizione tra complessi è interpretabile come una composizione di traslazioni, una moltiplicazione di un complesso per un numero reale è interpretabile come una omotetia; proviamo a interpretare geometricamente la moltiplicazione per i: • 1 per i sappiamo che fa i; quindi il "vettore 1" è stato ruotato di 90° • -1 per i sappiamo che fa -i; quindi il "vettore -1" è stato ruotato di 90°     Definiamo in modo analogo "i per i":   i, ossia (0,1), ruotato di 90° diventa il vettore 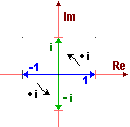(-1,0), che abbiamo rappresentato col numero complesso -1.

    Posto  i·i = -1  la moltiplicazione precedente diventa:

(7 + 10 i) · (4 + 3 i)  =  28 + 61 i + 30(-1)  =  -2 + 61 i

Indichiamo con z un generico numero complesso e con x e y le sue parti reale e immaginaria (z = x+iy). La figura sotto a sinistra illustra la interpretazione geometrica delle trasformazioni z → z+(4+3i) e z → z·(4+3i).

• z → z + (4+3i), in quanto (x+iy)+(4+3i) = x+4+(y+3)i, trasforma ogni punto (x,y) in (x+4,y+3): è la traslazione di vettore (4,3) che trasforma il quadrato F nel quadrato F1; • z → z · (4+3i) trasforma i punti del segmento OA nei punti del segmento OP; infatti O = 0+0i rimane invariato, A = 1+0i diventa 4+3i, ossia P; il punto medio di OA, ossia 0.5+0i, diventa 4/2+3/2i, cioè (4/2,3/2) che è il punto medio di OP, e così via. Facendo i calcoli in generale si ottiene:   z · (4+3i) = (4x-3y) + (4y+3x)i; quindi B = (1,1) diventa Q = (1,7), C = (0,1) diventa R = (-3,4); è facile verificare che il poligono OPQR è un quadrato: è il quadrato F2 che si ottiene da F mediante la stessa rotazione attorno ad O e la stessa omotetia (trasformazione di scala monometrica) che trasformano il versore OA dell'asse reale (il numero 1) nel vettore OP (il numero 4+3i).

  In sintesi, addizioni e moltiplicazioni tra numeri complessi si eseguono operando sulle espressioni che li rappresentano come si fa tra i numeri reali, a patto di operare la sostituzione di i² con -1.  E si ha che l'addizione di a+ib a x+iy trasla il vettore (x,y) con passi Δx=a e Δy=b e la moltiplicazione di x+iy per a+ib trasforma (x,y) con la stessa "roto-omotetia" che trasforma il vettore (1,0) in (a,b):  alla direzione di (x,y) viene addizionata la direzione di (a,b), il modulo di (x,y) viene moltiplicato per il modulo di (a,b).

    Viene chiamato modulo di a+ib, e indicato |a+ib|, il modulo del vettore (a,b), ossia √(a²+b²). Ad es. |4+3i| = √(16+9) = 5: è la lunghezza del segmento OP della figura precedente (ed è il fattore di scala dell'ingrandimento eseguito da z → z·(4+3i)).

    La direzione del vettore (a,b) viene invece chiamata anomalia o argomento di a+ib . Ad es. l'argomento di 4+3i è la direzione del vettore (4,3), ossia la direzione compresa tra 0° e 90° che ha come pendenza 3/4 = 0.75; per trovarne il valore posso usare ad es. una calcolatrice o del software:  atan(0.75) = 0.6435011, atan(0.75)*180/pi = 36.8699; 36.870° è la direzione del segmento OP della figura precedente (ed è l'ampiezza della rotazione eseguita da z → z·(4+3i)).

[con "calcolatrice2" (qui) ho  atan(3/4) [=] → 0.6435011087932844,  atan(3/4)*180/PI [=] → 36.86989764584402]

    Osserviamo che, se z è reale, |z| inteso come valore assoluto o come modulo coincidono in quanto √(x²+0²) = √(x²) = |x|. Del resto il modulo di OP indica la distanza di P da O, e, se P sta sull'asse x, questa non è altro che il valore assoluto dell'ascissa di P. 

    Come si possono effettuare i calcoli precedenti con WolframAlpha:

  Per calcolare le divisioni tra numeri complessi basta che stabiliamo, dato z = x+iy, quanto vale il reciproco 1/z. Infatti la divisione per z la possiamo interpretare come una moltiplicazione per 1/z.
    Dobbiamo, dunque, trovare a+ib tale che (a+ib)(x+iy)=1, ossia tale che:
ax-by + i(ay+bx) = 1, ossia:   ax-by=1 & ay+bx=0
    È un sistema di equazioni con incognite a e b che posso risolvere ad es. così:
a=-bx/y & (-bx²/y-by)=1     a=-bx/y & b(x²+y²)/y=-1
b=-y/(x²+y²) & a=x/(x²+y²)     Quindi:
1/z = 1/(x+iy) = (x-iy)/(x²+y²).
    Un modo più veloce (basato su ) per ottenere lo stesso risultato è il seguente:

1	=	x-iy	=	x-iy	=	x-iy
———		——————		———		———
x+iy		(x+iy)(x-iy)		x2- i2y2		x2 + y2

    Con WolframAlpha:

Esempio: calcolo di  (-2 + 61 i) / (4 + 3 i).  Potremmo usare la "formula" vista sopra, ma procediamo direttamente:

-2 + 61 i	=	(-2 + 61 i)(4 - 3 i)	=	175 + 250 i	=  7 + 10 i
————		——————		————
4 + 3 i		(4 + 3 i)(4 - 3 i)		42 + 32

    Con WolframAlpha:

Esercizi:   uno  e  soluz.;    due  e  soluz.;    tre  e  soluz.;    quattro  e  soluz.;    cinque  e  soluz.;    sei  e  soluz..
 

  Le coordinate polari

    Un vettore può essere individuato indicandone le componenti oppure indicandone direzione e modulo. Analogamente un numero complesso può essere individuato indicandone le parti reali e immaginaria oppure indicandone argomento e modulo. E tutto ciò è analogo alla possibilità di individuare un punto del piano mediante le sue coordinate cartesiane oppure mediante le sue coordinate polari. Queste sono comode, oltre che per rappresentare fenomeni, per descrivere figure.

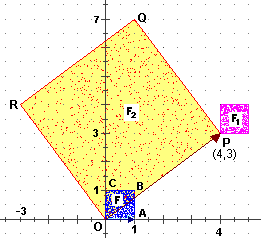
Ad es., usando ρ (lettera greca "ro") e θ (lettera greca "teta") per rappresentare rispettivamente la distanza da O e la direzione, il disco forato (corona circolare) illustrato a fianco, che in coordinate cartesiane è rappresentabile con 4 ≤ x²+y² ≤ 16, e che usando la variabile complessa z (=x+iy) può essere descritta con 2 ≤ |z| ≤ 4, usando le coordinate polari diventa  2 ≤ ρ ≤ 4: è la figura compresa tra i cerchi ρ=2 e ρ=4.     Sono facilmente descrivibili le spirali [se n'è visto un esempio alla voce tangenti e curve]. Quella raffigurata a destra è ρ = θ (per θ=0 ho ρ=0: sono nell'origine; al crescere di θ, ossia ruotando, ρ, ossia la distanza da O, cresce; per θ=2π ho compiuto un giro e sono a distanza 2π da O; per θ=4π ho compiuto un secondo giro e sono a distanza doppia da O; …).     La disequazione 135° ≤ θ ≤ 225° invece rappresenta un angolo. In forma cartesiana lo avremmo descritto con il sistema:  x ≤ 0 & h·x ≤ y ≤ k·x con h = tan(225°) e k = tan(135°).     ρ varia sui numeri reali non negativi, mentre θ varia su tutti i numeri reali. (la figura precedente è stata tracciate con questo script)

    Naturalmente due numeri θ₁ e θ₂ che differiscono di 2π (360°) sono da intendersi diversi come numeri ma uguali come direzioni.

    In alcuni casi si restringe θ a variare in [0,2π), cioè [0,360°), o in (-π,π], cioè (-180°,180°]. In questi casi le eventuali operazioni tra direzioni vengono interpretate in modo opportuno.

Le coordinate polari ρ e θ vengono chiamate spesso, rispettivamente, raggio vettore e anomalia (come viene spesso chiamato anche l'argomento del corrispondente numero complesso). L'origine del sistema di riferimento viene chiamata polo. Il termine anomalia deriva dall'aggettivo "anomalo" (strano, irregolare). Infatti tra i primi usi delle coordinate polari vi fu quello della descrizione del moto dei pianeti intorno al sole e la scoperta che la direzione del vettore Sole-Pianeta (ossia della anomalia) non variasse proporzionalmente al tempo (i pianeti descrivono un'orbita ellittica e "ruotano" più velocemente quando sono vicini al sole) era stata considerata una cosa "strana" rispetto all'idea allora predominante che i pianeti ruotassero attorno al sole in modo uniforme (ossia con il vettore Sole-Pianeta che varia direzione proporzionalmente al tempo).

  Se indichiamo con x, y, ρ, θ e con x_n, y_n, ρ_n, θ_n rispettivamente le parti reale e immaginaria, il modulo e l'argomento del numeri complessi z e z_n, possiamo scrivere:

se z = z₁· z₂,   ρ = ρ₁· ρ₂  e   θ = θ₁+ θ₂;

se z = 1 / z₁,   ρ = 1 / ρ₁  e   θ = –θ₁;

se z = z₁/ z₂,   ρ = ρ₁/ ρ₂  e   θ = θ₁– θ₂.

Naturalmente, ρ = |z|.  Se la direzione di z viene espressa con un numero θ tale che 0≤θ<2π, tale numero viene indicato con Arg(z) e chiamato argomento principale di z. A volte si ricorre a una convenzione diversa: si assume come Arg(z) tra i possibili argomenti di z (ossia tra i numeri con cui se ne può esprimere la direzione) quello che cade in (-π,π]. A 0 non è assegnato un argomento principale (il vettore nullo non è caratterizzabile con una particolare direzione: se si pone ρ=0, per qualunque θ risulta individuato il punto (0,0): se parto da O con una qualunque direzione ed eseguo uno spostamento nullo, rimango in O).

A lato è illustrato come le funzioni circolari mettono in relazione parti reale e immaginaria (coordinate cartesiane) con modulo ed argomento (coordinate polari).     Mentre da ρ e θ a x e y si passa con la diretta applicazione di due formule, e lo stesso accade per il passaggio da x e y a ρ, per determinare θ occorre tener conto che la direzione con pendenza y/x fornita da arctan (così, o atan, è indicata la funzione inversa della funzione tangente, tan) potrebbe differire di 180° dal valore corretto:  il valore fornito è sempre compreso tra -π/2 e π/2, per cui se x<0 occorre aggiungere π:

x=ρcos(θ)   y=ρsin(θ)     ρ=√(x2+y2)   tan(θ)=y/x

• nel caso di 2+5i (figura A), ρ = √(4+25) = √29 = 5.3851…, θ = atan(5/2) = atan(2.5) = 1.1902… = 68.198…°
• nel caso di -3+2i (figura B), ρ = √(9+4) = √13 = 5.3851…, θ₀ = atan(-2/3) = -0.588002… = -33.690…°, che non è l'argomento di -3+2i, in quanto dovrebbe essere una direzione del 2° quadrante: dobbiamo aggiungere π: θ = -0.588002…+π = (-33.690…+180)° = 146.310°

    Se x = 0, non si può calcolare arctan(y/x). Ovviamente si ha: θ = π/2 quando y > 0, θ = 3π/2 (o -π/2) quando y < 0.

Nota.  Le scritture arctan(x) e atnn(x) sono abbreviazioni di arcotangente di x (la direzione o angolo compreso tra -π/2 e π/2 che ha come tangente x). La parte "arco" della parola deriva dal fatto che, come è spiegato alla voce direzioni e funz. circolari, direzioni e angoli sono "quantificati" interpretandoli come lunghezze di archi di cerchio.  In modo simile sono chiamate le funzioni inverse di seno e coseno ("arcoseno", "arcocoseno").

    Con WolframAlpha:

 Numeri complessi, figure e loro trasformazioni

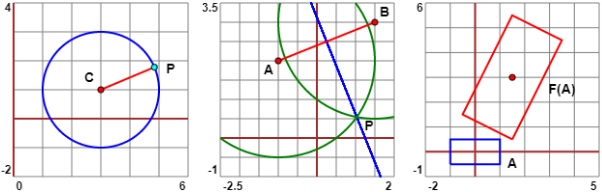
L'uso dei numeri complessi consente di descrivere in modo compatto diversi tipi di figure.  Ad es. il cerchio di centro C = (3,1) e raggio 2 (figura sotto a sinistra) può essere descritto dalla equazione |z-3-i|=2 con la "variabile complessa" z=x+iy, che traduce la condizione che il punto P = (x,y) abbia distanza 2 da C, ovvero che il vettore CP abbia modulo 2.  L'equazione |z+1-2i|=|z-1.5-3i| rappresenta invece l'asse del segmento di estremi A = ( 1, 2) e B = (1.5, 3)  (figura sotto al centro): un punto P (ovvero z) di esso è equidistante da A (ovvero -1+2i) e da B (ovvero 1.5+3i).

  Abbiamo visto che le trasformazioni geometriche tra figure piane possono essere descritte invece che come funzioni (x,y) → (x',y') da coppie di numeri reali a coppie di numeri reali anche come funzioni z → z' da numeri complessi a numeri complessi.  Sopra a destra è illustrata la trasformazione del rettangolo A mediante una funzione F ottenuta componendo z → z·(1+2i)  (la rotoomotetia che trasforma il versore dell'asse x nel vettore (1,2), e quindi i lati orizzontali di A, lunghi 2, in segmenti diretti e lunghi come il vettore (2,4))  e z → z+1.5+3i  (la traslazione di passi 1.5 e 3), ossia la funzione z → z·(1+2i)+1.5+3i.  Più in generale tutte le similitudini possono essere descritte come funzioni di variabile complessa del tipo z → z·z₁+z₂

Dato z = x+iy, si pone = x-iy.  È il numero che si ottiene cambiando segno alla parte immaginaria di z; viene chiamato il coniugato di z. Geometricamente, z → è la simmetria rispetto all'asse x  (la trasformazione in forma polare è: ρ' = ρ, θ' = -θ).     Invece z → -z = -x-iy è la simmetria rispetto a (0,0)  (in forma polare è: ρ' = ρ, θ' = θ+180°)..     Le rotazioni attorno ad O sono un caso particolare delle trasformazioni richiamate nel punto precedente: sono descrivibili come funzioni z → z·z1 dove z1 è un numero complesso di modulo 1, ossia un numero complesso che rappresenta un versore. Se voglio ruotare con ampiezza α moltiplico per il numero che rappresenta il versore di direzione α, ossia per cos(α) + i sin(α).

Usando le coordinate cartesiane questa trasformazione diventa: (x, y) → (x·cos(α)-y·sin(α), x·sin(α)+y·cos(α)),  infatti: z · (cos(α) + i sin(α)) = (x+iy)(cos(α)+isin(α)) = x cos(α) - y sin(α) + i (x sin(α) + y cos(α))     Non è una formula da imparare a memoria: la si ricava facilmente nel modo appena illustrato.

Nota. La relazione tra moltiplicazioni per un numeri complessi e rotazioni attorno ad O ci consente di ricavare facilmente alcune formule spesso utili quando si opera con funzioni circolari. Siano u e v due numeri complessi di modulo 1 e siano α e β i loro argomenti, ossia siano  u = cos(α) + i sin(α)  e  v = cos(β) + i sin(β). Allora:
u·v = (cos(α) + i sin(α))·(cos(β) + i sin(β)) = cos(α)·cos(β) + i·(sin(α)·cos(β)+sin(β)·cos(α)) + i²·sin(α)·sin(β) = cos(α)·cos(β)-sin(α)·sin(β) + i·(sin(α)·cos(β)+sin(β)·cos(α)).
D'altra parte u·v ha come argomento la somma degli argomenti di u e v, ossia:
u·v = cos(α+β) + i·sin(α+β).  Se ne deduce che:

cos(α+β) = cos(α)·cos(β) – sin(α)·sin(β),   sin(α+β) = sin(α)·cos(β) + sin(β)·cos(α).

[cliccando qui ottieni una figura che suggerisce una dimostrazione alternativa di tali relazioni]

Come caso particolare, per β = α, si ottiene:
cos(2α) = cos(α)² – sin(α)² = [essendo sin(α)²=1–cos(α)²]  2cos(α)² – 1,  sin(2α) = 2 sin(α)·cos(α).
Si possono ricavare facilmente, essendo tan(x) = sin(x)/cos(x):

tan(α+β) = (tan(α)+tab(β)) / (1–tan(α)·tan(β))  e  tan(2α) = 2 tan(α) / (1–tan(α)²)

[le formule …(2α) sono note come formule di duplicazione - double-angle formulas]

A lato, e sotto, è esemplificata l'azione di z → z2:  viene raddoppiato "θ" e viene elevato al quadrato "ρ", per cui ogni semicerchio centrato in O sopra all'asse x viene trasformato nel cerchio centrato in O con raggio elevato al quadrato, e lo stesso accade per il semicerchio simmetrico che sta sotto all'asse x.
Ad es. il punto (0,2), ossia 0+2i, viene trasformato nel punto (-4,0), ossia -4+0i: la direzione da 90° diventa 180° e il modulo da 2 diventa 4. Ma anche il punto (0,-2) del semicerchio inferiore, ossia 0-2i, viene trasformato nel punto (-4,0): la direzione da -90° diventa -180°, ovvero da 270° diventa 540° che, "come direzione", è uguale a 540°-360° = 180°, e il modulo da 2 diventa 4. Del resto, con i calcoli, abbiamo sia: (2i)2= 22 i2= 4·(-1) = -4, sia: (-2i)2= (-2)2 i2= 4·(-1) = -4.     Geometricamente (vedi figura (A) sotto) possiamo interpretare anche il fatto noto che non solo 1 ma anche -1 elevato al quadrato fa 1 (-1 ha θ=180°, per cui moltiplicare per -1 equivale a ruotare di 180°, e quindi -1 per sé stesso diventa 1).  In (B) è invece illustrato che sia i che -i al quadrato fanno -1 (i ha direzione 90°, il suo doppio è 180°, che è la direzione di -1;  -i ha direzione -90° il cui doppio è -180°, che è un altro modo di esprimere la direzione di 180°).  La figura (C) illustra in un modo alternativo che -i al quadrato fa -1 (la direzione di -i posso indicarla con 270° il cui doppio è 540° che, come si è già osservato, equivale a 180°).
Più in generale ogni punto e il suo simmetrico rispetto ad O sono trasformati da z → z2 nello stesso punto. Del resto, (-z)2 = (-1)2z2 = z2.     Come nel caso in cui x sia un numero reale positivo con √x (radice quadrata di x) si indica uno dei due numeri (quello positivo) che al quadrato fanno x, così, più in generale, se z è un numero complesso, con √z si indica uno dei numeri complessi che al quadrato fanno z, e precisamente quello con direzione in (-90°, 90°].  In particolare con √(-1) si indica i, non -i.

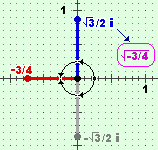
E, per esempio, come √(-3/4), si prende √3/2i  [per le proprietà delle potenze, il suo quadrato è il quadrato di √3/2 per il quadrato di i, ossia 3/4·(-1) = -3/4],  non il suo opposto -√3/2i, che anch'esso al quadrato fa √(-3/4).  In pratica si procede così:                     √(-3/4) = √(3/4·(-1)) = √(3/4)·√(-1) = √3/2i.     Posso , invece, dire che  z2= -3/4  ha come soluzioni entrambi i numeri, ossia ±√3/2i.. Ecco come tracciare figure, come la prima del paragrafo, con uno script   →

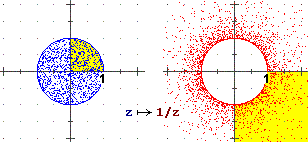
  La figura sotto a sinistra illustra un'altra trasformazione, z → 1/z, che, ricordando la interpretazione "polare" del prodotto, possiamo descrivere anche così:  ρ' = 1/ρ,  θ' = – θ  (infatti z e 1/z per avere come prodotto 1, ossia un numero che ha 1 come modulo e 0 come argomento, devono avere moduli ρ e ρ' che abbiano come prodotto 1 e argomenti θ e θ' che abbiano come somma 0, o, che è lo stesso, 360°):  i punti all'interno del "cerchio goniometrico" vengono trasformati in punti esterni, e viceversa, e tutti i punti vengono ribaltati rispetto all'asse y.

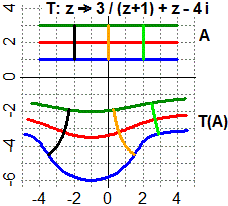    Nella figura sopra a destra si vede come una particolare funzione a input e output complessi trasforma un reticolato: si vede che cambia la forma ma che le linee tra loro perpendicolari si mantengono perpendicolari. Quella di mantenere gli angoli con cui si incontrano le linee è una caratteristica delle trasformazioni descrivibili come z → z' con z' termine ottenuto componendo le quattro operazioni (e altri particolari tipi di funzione). È di questo genere anche la funzione che trasforma la figura F nella figura D nell'esempio all'inizio della voce trasformazioni geometriche.

    Si può intuire come questo tipo di trasformazioni (chiamate "conformi", in quanto conservano la forma degli incroci) possano essere utili per studiare come cambia il flusso di un fluido al cambiare della forma di un canale, per studiare questioni di aerodinamica e altri fenomeni di tipo fisico:  una situazione in cui il comportamento di una grandezza vettoriale (una velocità, una forza, …) varia lungo certe linee può essere ricondotta ad una in cui le linee lungo cui agisce la grandezza siano più facili da rappresentare e, quindi, consentano di semplificare lo studio matematico del problema.

A destra un esempio di come un cerchio può essere trasformato dando luogo a delle curve particolarmente belle. In questo caso si viene a formare un nodo in O. Vediamo come trovare quali sono i punti del cerchio che vengono trasformati in O, ossia quali sono i valori di z per cui:       z2+ z + 1 = 0. Potendo operare in C come se si fosse in R, posso ricorrere a un completamento del quadrato: (z + 1/2)2- 1/4 + 1 = 0   →   (z + 1/2)2 = -3/4   →  [vedi sopra] z + 1/2 = i √(3/4)  OR  z + 1/2 = -i √(3/4) z = -1/2 + i √3/2  OR  z = -1/2 - i √3/2.

(-1/2, √3/2) e (-1/2, -√3/2) sono dunque i due punti che vengono trasformati nell'origine degli assi. La cosa può essere anche interpretata geometricamente, come illustrato a sinistra nel caso di z rappresentato dal punto (-1/2, √3/2): la trasformazione in z2 produce mediante una rotazione un punto che poi, con la traslazione corrispondente a "+z" diventa (-1,0) e, infine, con "+1" diventa l'origine.

Vedi qui lo script con cui è stato ottenuto il grafico.

 Polinomi rispetto a una variabile complessa

Quando per descrivere il piano invece delle coordinate cartesiane si usano i numeri complessi si parla di piano di Argand, dal nome del matematico francese che, verso la fine del XIX sec., ha avuto l'idea di usare i numeri complessi per descrivere figure e trasformazioni geometriche, e, in particolare, di rappresentare le rotazioni di 90° come moltiplicazioni per i.
    Ma i numeri complessi sono stati "inventati" nel XVI sec. come "trucco" per risolvere alcune equazioni polinomiali di 3° grado. Il procedimento è stato descritto in quegli anni dall'italiano Gerolamo Cardano, anche se probabilmente non è stato lui ad avere l'idea iniziale. Il termine numeri immaginari fu introdotto (circa 100 anni dopo) da Cartesio, e il simbolo i fu introdotto (dopo circa altri 100 anni) da Eulero (prima si usavano altri nomi e altre notazioni).

Si era trovato che un'equazione del tipo  x³ + p x + q = 0  ha come soluzione rispetto ad x il numero  ³√(R-q/2) - ³√(R+q/2)  dove  R = √((p/3)³+(q/2)²)
    Ad esempio per  x³ + 6 x - 2 = 0  si trova  R = √(2³+1²) = √9 = 3  da cui  x = ³√4 - ³√2. È possibile verificare (anche con una calcolatrice) che si tratta effettivamente di una soluzione.
   Ma per  x³ - 15 x - 4 = 0  si trova  R = √(-5³+2²) = √(-121), che non sarebbe definito, mentre si sa che una soluzione ci deve essere (le funzioni polinomiali di 3° grado assumono valori sia positivi che negativi quindi ci si aspetta che assumano anche il valore 0). Si è allora provato a inventare i per indicare √(-1) e vedere se con qualche manipolazione algebrica si riesce a ricavare la soluzione.
√(-121) diventa 11i e la soluzione diventerebbe x = ³√(2 + 11i) - ³√(2 - 11i)
    Si trova che (2+i)³ = (2+i)(2+i)(2+i) = (4+4i-1)(2+i) = (3+4i)(2+i) = (6+11i-4) = 2+11i  e analogamente che (2-i)³ = 2-11i, per cui si ha:
x = ³√(2 + 11i) - ³√(2 - 11i) = 2+i - 2-i = 4, che è effettivamente una soluzione della nostra equazione.

  Dunque, i numeri complessi sono stati introdotti come "numeri fittizi" per potere estendere l'uso delle formule risolutive di alcune equazioni polinomiali e trovare i numeri reali che le risolvono. Non c'era, invece, alcun interesse a trovare i numeri complessi che risolvono una equazione, interesse che è nato, invece, con gli usi dei numeri complessi descritti nei paragrafi precedenti, in cui si è avuto a che fare con equazioni polinomiali di variabile complessa, come la equazione z²+ z + 1 = 0 risolta sopra. Si possono considerare complessi non solo la variabile, ma anche i coefficienti, come nel caso dell'equazione z²- i = 0, ossia z² = i (che ha come soluzioni cos(45°)+isin(45°) e il suo opposto).
    Ai polinomi di variabile complessa si può applicare lo stesso algoritmo della divisione e lo stesso teorema del resto visti per quelli di variabile reale.
    In più per essi vale il cosiddetto teorema fondamentale dell'algebra, secondo il quale ogni equazione polinomiale di variabile complessa di grado maggiore o uguale a 1 ha almeno una soluzione.
    Ad esempio, x²+ 1 = 0 se le si assegna come dominio R non ha soluzioni, se le si assegna come dominio C (caso in cui, in genere, verrebbe scritta come z²+ 1 = 0) ha invece i come soluzione, e anche -i.
    Dal teorema del resto e dal teorema fondamentale deriva la possibilità di scomporre, nell'ambito dei numeri complessi, qualunque polinomio P(z) di grado n, con n≥1, nel prodotto di n polinomi di grado 1. Infatti trovata una soluzione z₁ posso dividere P(z) per z-z₁ e, trovato Q₁(z) come quoziente, scrivere P(z) come (z-z₁)Q₁(z); poi, trovata una soluzione z₂ di Q₁(z), posso scriverlo come (z-z₁) (z-z₂)Q₂(z); e così via fino a ottenere (z-z₁) (z-z₂)… (z-z_n), eventualmente moltiplicato per il coefficiente direttivo di P(z).
    Ovviamente se, ad esempio, z₁ e z₂ sono eguali, potremo sostituire (z-z₁)(z-z₂) con (z-z₁)² (in questo caso si dice che la radice z₁ ha molteplicità 2).

  Questo è il motivo per cui i programmi che svolgono calcoli simbolici in genere svolgono le loro manipolazioni operando nei numeri complessi: in tale ambito è sempre possibile fattorizzare i polinomi per i quali si conoscono formule risolutive delle corrispondenti equazioni e, quindi, è più facile semplificare un'espressione complessa contenente termini polinomiali.
    Ciò, tuttavia, crea anche dei problemi. Infatti può accadere che una semplificazione eseguita nell'ambito dei numeri complessi conduca a un termine che non è equivalente nell'ambito dei numeri reali.

Ad esempio alcuni software della funzione  F: x → x-1+√(4x)/√x  tracciano il grafico anche in (-∞,0) anche se ivi F non definita:  durante la tabulazione per tracciare il grafico calcolano la radice anche dei numeri negativi, trasformano "i/i" in 1 e trovano un numero reale come valore della funzione  (ad esempio per x = -1 trovano -1-1+√(-4)/√(-1) = -2+2i/i = -2+2 = 0).  Per essi, infatti, F(x) equivale a  x+1 = 0  (ossia come se, nella figura a lato, F fosse prolungabile in G)  in quanto considerano √(4x)/√x, ossia 2√x/ √x, equivalente a 2 per ogni x diverso da 0, anche per x < 0.     E se chiedessi di risolvere l'equazione  F(x) = 0  otterrei come soluzione -1 anche se non lo sarebbe in quanto non appartiene al dominio della equazione, se pensata di variabile reale  (apparterrebbe ad esso se considerassi l'equazione nell'ambito dei numeri complessi).

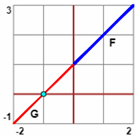    Anche WolframAlpha con  plot x-1+sqrt(4*x)/sqrt(x), x in [-2,2], y in [-1,4]  produce il grafico sottostante a sinistra.
    plot Piecewise[ { {x-1+sqrt(4*x)/sqrt(x), x>=0}, {1e5, x<0} } ], x in [-2,2], y in [-1,4]  fornisce invece il grafico corretto, a destra;  abbiamo definito la funzione a tratti:  per x = 0 la funzione effettiva,  per x < 0 un valore molto grande, fuori dall'intervallo delle y scelto.

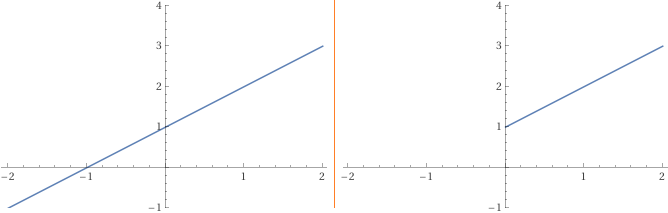
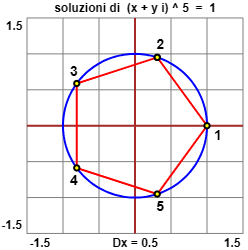
È interessante osservare che le soluzioni di zn = 1, con z variabile complessa, corrispondono geometricamente ai vertici del poligono regolare centrato nell'origine e avente un vertice in (0,1).     A lato è illustrato il caso  z5 = 1:  oltre a 1 è soluzione  cos(360°/5) + i sin(360°/5)  in quanto elevare alla 5 equivale a moltiplicare "θ" per 5 e quindi ottenere  cos(360°) + i sin(360°)  che è uguale ad 1;  ma è soluzione anche  cos(360°/5·2) + i sin(360°/5·2)  in quanto  360°/5·2·5 = 360°·2  che, come direzione, equivale a  360°;  e così via. (la figura a destra è stata tracciata con questo script)

Altri esercizi:   testo   e   soluz.;     testo   e   soluz.;     testo   e   soluz.;     testo   e   soluz..