Derivata e differenziale di una funzione

Alle voci  pendenza 2,  rette tangenti e curve e  velocità di variazione vengono proposte diverse situazioni e idee che motivano e introducono il concetto di derivata, uno dei più importanti della matematica.  Esamina almeno l'ultima di tali voci prima di intraprendere la lettura di questa.

  Introduzione

    Riprendiamo i primi tre esempi discussi nella voce velocità di variazione.
    Nell'esempio iniziale abbiamo visto come l'esame della pendenza di un grafico consenta di discutere efficacemente della velocità con cui varia un fenomeno, in questo caso della velocità con cui cambia la temperatura in una certa località.
    Nel secondo abbiamo considerato un fenomeno in cui la pendenza del grafico cambia con continuità, in un modo che intuiamo possa essere descritto con una funzione.
    Nel caso del fenomeno considerato nel terzo esempio possiamo trovare la pendenza dei tre tratti che ne costituiscono il grafico. Nei due punti che corrispondono a V=1000 e a V=1500 la pendenza varia di scatto:  ad esempio a sinistra di V=1000 è 50/1000 = 0.05, a destra è 50/500 = 0.1.

Consideriamo, ora, un esempio astratto.     A lato è tracciato il grafico della funzione F che ad x associa x².     Quale è la pendenza della tangente al grafico nel punto di ascissa 1, tracciata in blu nella figura?     Nel primo grafico è evidenziato, oltre al punto del grafico di ascissa 1, quello di ordinata 4.  La retta che passa per questi due punti ha pendenza "variazione di y"/"variazione di x" = 3/1 = 3.     Nel secondo grafico è evidenziato il punto di ordinata 2.  Qual è la pendenza della retta che passa (1,1) e questo punto. L'ascissa x di questo punto è la soluzione di x²=2, ossia √2, per cui la pendenza è 1/(√2-1) = 2.4142…     Procedendo con punti man mano più vicini a (1,1) potremmo trovare valutazioni mano mano più precise della pendenza della tangente. Si intuisce, comunque, che tale pendenza è 3/1.5 = 2  (lo dimostreremo più avanti).     Consideriamo la funzione rappresentata in basso a destra, la funzione inversa della restrizione di F agli input non negativi, ossia la funzione G che ad x associa √x.     Il grafico di G è ottenuto da quello di F scambiando le x con le y.  Quindi la pendenza della tangente in un punto del grafico di G è il reciproco della pendenza della tangente al grafico di F nel punto simmetrico rispetto alla bisettrice del 1º quadrante.     Nel caso particolare del punto (1.1), che sta su tale bisettrice, il simmetrico coincide col punto stesso. La pendenza è il reciproco di 3/1.5 (= 2), ossia 1.5/3 (= 1/2).

    Vediamo, ora, come precisare le idee introdotte con questi esempi.

    Avrai sentito parlare di "tasso tendenziale di inflazione", "aumento tendenziale della produzione", ….  Si tratta di indicatori economici con cui si cerca di descrivere la situazione attuale e individuare come essa evolverebbe se le cose continuassero ad andare come negli ultimi tempi.  Analogamente, se nell'ultimo anno la temperatura media sulla Terra fosse salita di 0.04° potremmo dire che questa è la tendenza con cui varia la temperatura sul nostro Pianeta; potremmo prevedere che tra 5 anni la temperatura sarà variata di 0.04·5 = 0.2 gradi.  Ma in entrambi i casi si tratta solo di approssimazioni di come evolveranno i fenomeni, che saranno tanto migliori quanto più la produzione o la temperatura della terra varieranno proporzionalmente allo scorrere del tempo; e questo avverrà con una buona approssimazione solo per durate relativamente piccole.

    In generale, data una funzione F (continua) di una generica variabile x , possiamo considerare la variazione tendenziale di F(x), ossia la variazione che F(x) subirebbe passando da x a x+Δx se in tale intervallo le variazioni dell'output fossero proporzionali a quelle dell'input, cioè se la funzione proseguisse con grafico rettilineo, cioè se fosse lineare.  Viene usato il termine differenziale di F(x), e la notazione d F(x), per indicare la variazione tendenziale di F(x).
    Nella figura seguente la funzione che ha tale retta come grafico è indicata T. La variazione dell'input per F (inidicata con Δx) e per T (indicata con dx) sono ovviamente uguali.
    La retta considerata è tangente al grafico di F nel punto P di esso avente ascissa x.

Il differenziale di F  (nel punto x e rispetto alla variazione Δx).
Per Δx → 0  dF(x) ≈ ΔF(x).

La mia approssimazione di ΔF(x)  - la variazione effettiva di F(x) -  con d F(x)  è buona se Δx è piccolo, man mano peggiora al crescere di Δx.     Rivediamo il caso di √x.     Abbiamo visto che la retta tangente in (1,1) ha pendenza 1/2.  Approssimo il grafico di x → √x con essa e indico con E l'errore che commetto con questa approssimazione.  Se non dispongo di una calcolatrice posso valutare √2.5 tenendo conto che la retta tangente per x = 2.5 ha y = 1.5. Questa è l'approssimazione.  Il valore estatto sarebbe √2.5 = 1.581….  Quindi l'errore dell'approssimazione è E = 0.081…     Analogamente valutiamo, ad esempio, √0.9:  0.9 = 1-0.1.  La retta tangente in 1 se mi sposto a sinistra di 0.1 scende di 1/2·0.1 = 0.05.  Quindi posso approssimare √0.9 con √1-0.05 = 0.95.  Il valore esatto sarebbe √0.9 = 0.9486…  L'errore di questa approssimazione è molto piccolo: 0.0013…

Esercizio,     soluzione

  Definizione di coefficiente differenziale e di funzione derivata

    Abbiamo visto in un caso specifico come individuare la funzione lineare che ha grafico tangente ad una funzione in un dato punto.  In una precedente voce [ rette tangenti e curve] avevamo considerato le tangenti a curve che non fossero necessariamente grafici di funzioni.  Ora vediamo come si può determinare in generale il coefficiente direttivo della retta tangente al grafico di una funzione continua in un determinato punto x₀.
    Si chiama coefficiente differenziale o derivata di F in x₀ la pendenza della retta a cui tende la retta PQ sotto raffigurata (P è il punto del grafico di F di ascissa x₀ e Q è quello di ascissa x₀+h) al tendere di h a 0 (con h abbiamo indicato, per brevità, la variazione Δx dell'input):

lim h → 0	F(x0 + h) – F(x0)
	———————
	h

Δx = h    ΔF(x) = yQ – yP = F(x0 + h) – F(x0) P = (x0, F(x0))    Q = (x0+h, F(x0+h))

Nota. Nelle immagini abbiamo considerato variazioni h positive, ma è da intendersi che può essere anche h < 0, come nella figura a lato.  Il numero ( F(x0+h)−F(x0) )/h, che esprime la pendenza media del grafico di F tra x0 e x0+h, viene chiamato anche rapporto incrementale di punto iniziale x0 e passo h (è il rapporto tra la variazione dell'output e l'incremento dell'input, o il suo decremento, se h è negativo).

Esempio.  Sia F(x) = x². Determiniamo la derivata di F in 0.5. lim h→0  (0.5+h)² - 0.5² —————— h  =  lim h→0  0.25+h+h²-0.25 —————— h  =  lim h→0  h+h² —— h  =  lim h→0 (1+h)  =  1  Dunque per x→1/2 la funzione è approssimabile con una funzione lineare di coefficiente direttivo 1: T(x) = 1·(x − 0.5) + 0.25

    La derivata di una funzione F (a 1 input e 1 output, e continua) si chiama così in quanto deriva, si ottiene da F.  La derivata di F viene di solito indicata F'.  L'operazione di ottenere F' da F viene chiamata derivare F.  La funzione originaria si chiama primitiva (o antiderivata) della nuova funzione così ottenuta,  ossia F è una primitiva di F'.  La parola "derivata" ora viene usata per indicare il coefficiente differenziale ma inizialmente il nome era usato solo per indicare la funzione-derivata.

    Alla voce  pendenza 2 è stato introdotto in modo intuitivo, con vari esempi, il concetto di funzione-derivata. Esso in qualche modo generalizza il passaggio dal profilo altimetrico di una strada (grafico superiore) al grafico di come varia la sua pendenza (grafico inferiore):

–  Quando il percorso sale la pendenza è positiva. –  Nei punti in cui il percorso è orizzontale la pendenza è 0. –  Quando il percorso scende la pendenza è negativa. –  Quando la salita si addolcisce o la discesa si accentua la pendenza scende. –  Quando la discesa si addolcisce o la salita si accentua la pendenza sale.

Il grafico inferiore rappresenta la funzione derivata della funzione rappresentata sopra. Il grafico superiore rappresenta una funzione primitiva della funzione rappresentata sotto.

  Alcuni esempi di calcolo di derivate

    Vi sono alcuni casi semplici in cui è immediato determinare la funzione derivata.  Se una funzione F è costante (ad es. la temperatura in un buon frigorifero in funzione del tempo, a patto che esso non venga mai aperto), del tipo F(x) = k, al variare dell'input (x = tempo) si ha sempre lo stesso output (la stessa temperatura); quindi ΔF(x) vale sempre 0. Sia da questo fatto che dal fatto che si tratta di un grafico orizzontale e quindi con pendenza nulla, possiamo subito dedurre che F'(x) = 0 per ogni x.
    Se la funzione, invece, ha uscite che crescono proporzionalmente al crescere dell'input (ad es. il peso di un contenitore cilindrico al variare dell'acqua in esso contenuta), ossia se è una funzione polinomiale di 1° grado, del tipo F(x) = ax + b, la funzione derivata dovrà avere un valore costante e positivo (ad ogni tot di acqua in più corrisponde un altro tot di peso in più, indipendentemente da quanta acqua ci fosse prima).  La cosa può essere dedotta più precisamente pensando al grafico:  è una retta inclinata;  la sua pendenza è la derivata: F'(x) = a per ogni x.  In altre parole la funzione lineare che approssima F è F stessa, che ha come coefficiente direttivo a.

Esempio A.  Determiniamo la funzione derivata di x → x².
    Possiamo procedere come nel precedente paragrafo, con un generico x al posto di 0.5.

lim h→0  (x + h)2 – x2 ————— h

=

lim h→0  x2 + 2xh + h2 – x2 ——————— h

=

lim h→0  2xh + h2 ——— h

=

lim h→0 (2x+h)

=

2x

Esempio B.  Determiniamo la funzione derivata di x → x³.

lim h→0  (x+h)3 – x3 ———— h

=

lim h→0  x3+3x2h+3xh2+h3 – x3 ————————— h

=

…

=

lim h→0 (3x2+3xh+h2)

=

3x2

Esempio C.  Determiniamo la funzione derivata di x → xⁿ (per n intero positivo).

lim h→0  (x+h)n – xn ———— h

=

lim h→0  xn+nxn–1h+(…)h2 – xn ————————— h

=

…

=

lim h→0 (nxn–1+(…)h)

=

n xn–1

Nello sviluppo di (x+h)ⁿ, ossia nel calcolo del prodotto tra n fattori (x+h)(x+h)…(x+h), compare la somma di n termini uguali a x^n–1 h; tutti gli altri termini, a parte xⁿ, contengono h con almeno grado 2.

I grafici di alcune funzioni x → xⁿ e delle loro derivate:

    Usando D per indicare l'operazione di derivazione, possiamo esprimere la regola precedente con:

    Evitiamo di dimostrare che la regola si può estendere dai numeri naturali n ad ogni numero reale α:

Quindi:     D_x(x^2.5) = 2.5·x^1.5       D_x(√x) = D_x(x^1/2) = 1/2·x^−1/2       D_x(1/x) = D_x(x⁻¹) = −1·x⁻²

    Ci limitiamo a verificarlo graficamente nel caso degli ultimi due esempi tracciando (in blu) il grafico della funzione e (in rosso) quello della sua funzione derivata.

    Nel primo caso si vede per x che si avvicina a 0 la pendenza tende all'infinito, e infatti il grafico rosso tende a salire oltre ogni limite, e che per x = 1 la pendenza è 1/2, in accordo con quanto visto nel paragrafo precedente.
    Nel secondo caso si vede per x che si avvicina a 0 da destra la pendenza, negativa, ha valore assoluto che tende all'infinito e che per x che si avvicina a 0 da sinistra la pendenza, positiva, ha valore assoluto che tende all'infinito; per x che tende all'infinito o a meno infinito la pendenza tende a diventare zero.

    Qui puoi trovare gli script che producono i precedenti grafici:  uno,  due.

Esercizio,     soluzione

  Derivabilità e continuità

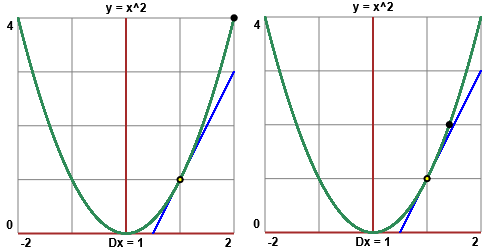
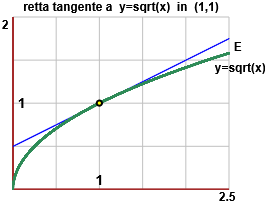
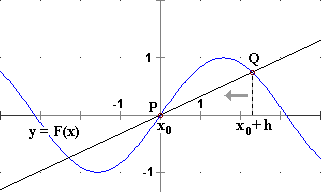
I concetti di derivata e differenziale sono stati introdotti per studiare come al variare dell'input varia l'output di una funzione continua. Non è detto, comunque, che una funzione continua in un intervallo sia derivabile in tutti i punti interni ad esso.     Consideriamo ad esempio la funzione x → |x|. Per x<0 e per x>0 si comporta in entrambi i casi come una funzione lineare, a sinistra di pendenza –1, a destra di pendenza 1. Le funzioni costanti che assumono questi valori costituiscono la sua derivata in (-∞,0) ∪ (0,∞), ma essa non è definita in 0 (per gli altri input coincide con la funzione segno). 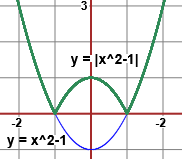       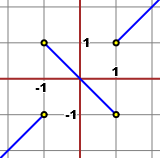Ecco, a sinistra, un altro esempio di funzione continua non ovunque derivabile, con il grafico avente 2 punti angolosi; a destra il grafico della sua derivata.     Oltre a casi come questi, in cui vi sono punti in cui la funzione non è derivabile in quanto ivi i limiti da destra e da sinistra delle derivate sono diversi, vi sono situazioni in cui il limite della derivata è infinito, ossia la tangente è una retta verticale, e situazioni in cui il limite della derivata, da destra o da sinistra o da entrame le parti, non esiste, come nell'esempio di curva  che presenta un punto avvicinandosi al quale aumenta la frequenza delle oscillazioni  visto alla voce  lunghezza: non si sa con che direzione si arriva e con quale si riparte da esso.       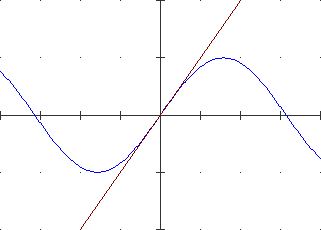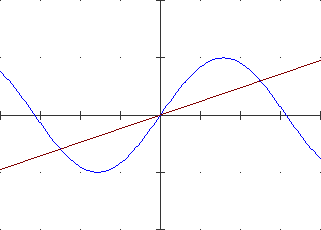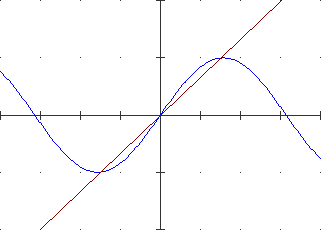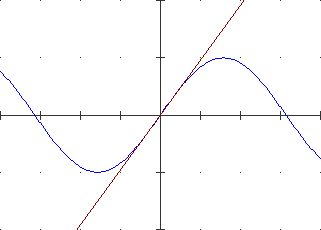Vi sono anche situazioni come quella illustrata nella figura seguente (e discussa in uno dei successivi esercizi), in cui il grafico della funzione avvicinandosi a un punto (l'origine) aumenta la frequenza con cui oscilla, per cui i limti da destra e da sinistra della derivata non esistono, ma in cui esiste la tangente nel punto (nel caso illustrato si tratta dell'asse x, ossia in 0 la funzione ha derivata 0).  Questo esempio mostra che il fatto che una o entrambe le derivate da destra e da sinistra in un punto non esistono non è sufficiente per stabilire che la derivata non esiste. Esercizi:   testo e soluzione,   testo e soluzione     Notazioni e proprietà     Abbiamo visto che, data una funzione f, la sua funzione derivata si indica f', dove l'apice "'" sta a indicare che si tratta di una nuova funzione rispetto a f. Ma esistono anche altre notazioni, in alcuni casi più utili di questa. 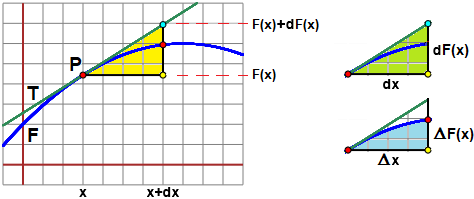Ecco le notazioni più usate per indicare la derivata di f in x (le ultime due si usano se si è convenuto di indicare f(x) con y): f '(x) ( f(x) )'x D(f)(x) Dx ( f(x) ) d f(x) —— d x y '(x) d y — d x (a) (b) (c) (d) (e) (f) (g)     Può essere comodo pensare la notazione d f(x) /d x come una abbreviazione di  limΔx→0 Δf(x)/Δx,  che è un modo in cui può essere riscritta la espressione con cui abbiamo definito D(f):  sarebbe il rapporto tra Δf(x) e Δx quando questi diventano piccolissimi, "infinitesimali":  d v indicherebbe una variazione infinitesimale della variabile v.     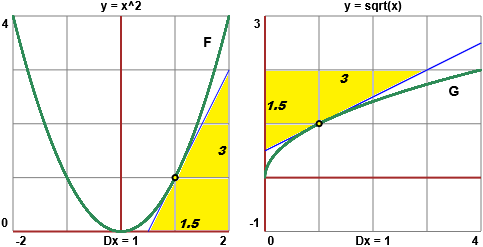Le formule seguenti, in cui f e g sono funzioni e k è un numero, presentano due proprietà di base delle derivate che facilitano il calcolo delle derivate di vari tipi di funzioni (con esse e quanto visto nell'esempio F siamo in particolare in grado di derivare tutte le funzioni polinomiali): D(kf) = kD(f) D(f+g) = D(f)+D(g) Dx(k f(x)) = k Dx(f(x)) Dx(f(x)+g(x)) = Dx(f(x)) + Dx(g(x))     Ne vediamo un esempio d'uso e poi le motiviamo: Dx(3x2 + 2√x) = Dx(3x2) + Dx(2√x) = 3Dx(x2) + 2Dx(√x) = 3·2x + 2·1/(2√x) = 6x + 1/√x     Abbiamo usato la seconda proprietà, poi la prima e, infine,  Dx (xα)  =  α xα–1.     La validità di queste formule è facilmente giustificabile: • Se, al variare di x, f(x) varia di una quantità Q, allora, alla stessa variazione di x, k·f(x) varia di k·Q. In breve:  Δ(k·f(x)) = k·Δf(x).  In termini geometrici: se moltiplico tutte le y per k la pendenza si moltiplica per k. • Se, al variare di x, f(x) varia di una quantità Q e g(x) varia di una quantità R, allora, alla stessa variazione di x, f(x)+g(x) varia di Q+R. In breve:  Δ((f+g)(x)) = Δf(x)+Δg(x).  In termini geometrici: se sommo, in corrispondenza delle stesse x, le y dei grafici di f e di g, ottengo un grafico che man mano ha come pendenza la somma delle pendenze dei due grafici. Attenzione 1.  Dx(7√x) = 7Dx(√x)   ma  Dx(√(7x))  non equivale a  7Dx(√x). Attenzione 2.  Prima di mettersi ad usare delle formule conviene sempre ragionare.  Per un esempio banale si pensi a  d/dx (F(x)+G(x))  con F(x)=|x|  e  G(x)=−|x|+1.  Uno potrebbe pensare che la derivata in 0 non esiste in quanto non esistono quelle di F e di G  (il cui grafico in 0 ha dei punti angolosi).  Ma il fatto che non esistano F'(x) e G'(x) non implica che non esista  d/dx (F(x)+G(x)).  In questo caso  (F+G)(x)  vale 1 per ogni x, e quindi la sue derivata vale, ovunque, 0. Un semplice esempio d'uso:  troviamo il vertice della parabola di equazione y = x² − 6x + 1/7 e, quindi, scriviamola nella forma y = (x−h)² + k. Dx(x² − 6x + 1/7) = 2x−6.  Il vertice della parabola ha ascissa x tale che 2x−6=0, ossia x = 3. Quindi la parabola ha la forma  y = (x - 3)² + k.  (x - 3)² + k = x²-6x+9+k = x²-6x+1/7 se 9+k=1/7, ovvero k = 1/7-9 = -62/7. La parbola possiamo esprimerla come y = (x - 3)² - 62/7. Si può verificare la cosa con WolframAlpha:           x^2 - 6x + 1/7 = (x-h)^2+k   →   h = 3, k = -62/7 Esercizio,   soluzione     Vedremo altre proprietà in una voce successiva.   Applicazioni: tangenti, andamento di funzioni, velocità, accelerazione     Le applicazioni del concetto di derivata sono innumerevoli. In questa voce abbiamo visto come può essere usato per fare approssimazioni e calcoli approssimati.  In una voce successiva si vedrà che esso consente, più in generale, di trovare funzioni polinomiali per approssimare funzioni continue di qualunque tipo.   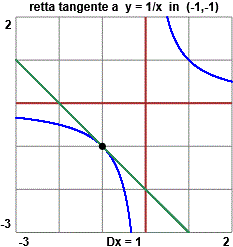Può essere impiegato per determinare le tangenti a una curva in un punto.  Ne abbiamo accennato introducendo la definizione di derivata. A destra è tracciata la tangente alla curva y=1/x nel punto di ascissa -1.  Per determinarla: • ne ho trovato la pendenza derivando la funzione: (1/x)' = (-1/x2) vale -1 per x=-1; • poi ho trovato la retta passante per (-1,-1) di pendenza -1:  è y = -x-2.     La questione può essere approfondita a partire da un'esame della voce  rette tangenti e curve. Vediamo ad es. un modo per determinare la tangente alla curva  x = t(t+1), y = t3  nel punto corrispondente a t=–1 alternativo a quello ivi considerato: Δy e Δx avvicinandosi al punto sono sempre meglio approssimabili con i differenziali rispetto a t  dy = d(t3)dt = 3t2dt  e  dx = d(t(t+1))dt = d(t2+t)dt = (2t+1)dt,  il cui rapporto, 3t2/(2t+1), vale –3 per t = –1.  Quindi –3 è la pendenza della retta tangente.      Il concetto di derivata, in quanto ci permette di determinare la pendenza di un grafico, ci consente di affrontare facilmente anche alcuni problemi legati all'andamento delle funzioni, sui quali torneremo. Ad es. se D(F) in un intervallo è sempre positiva, tranne che in un qualche isolato punto interno all'intervallo in cui vale 0, posso concludere che F è (strettamente) crescente nell'intervallo; è di questo tipo, ad es., x → x3, che ha 3x2 come derivata in x: questa è sempre positiva, tranne che per x=0 quando vale 0. 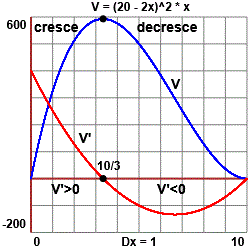       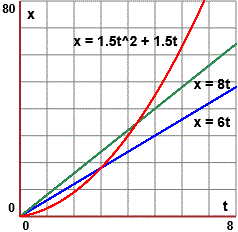Per fare un esempio concreto rivediamo il problema si rendere massimo il volume V = (20-2x)2x di una scatola alta x cm da realizzare con un quadrato di lamiera di lato 20 cm, considerato alla voce risoluz. equazioni 2. Là con un metodo grafico viene trovata come soluzione x = 3.33. Ora, disponendo del concetto di derivazione, possiamo fare: V' = D((20-2x)2x) = D(4x3-80x2+400x) = 12x2-160x+400 e studiare il segno di V', ovvero, dividendo per 4, sudiare il segno di 3x2-40x+100. Questa è una funzione quadratica con coefficiente direttivo positivo che si annulla in 40/6-√(1600-1200)/6 e in 40/6+√(1600-1200)/6, ossia in 10/3 e in 10. Ciò ci consente di concludere (vedi figura a lato) che V cresce per x ≤ 10/3 e decresce per 10/3 ≤ x ≤ 10. Quindi, nell'intervallo [0,10] che ci interessa (quello in cui può variare l'altezza della scatola), V assume valore massimo quando x = 10/3 = 3.333…, valore che, poi, dobbiamo approssimare tenendo conto del contesto del problema. Nota.  Una funzione che in un intorno del valore m assuma valore massimo in m stesso si dice che ha ivi un massimo relativo, nel senso che, al di fuori di tale intervallo, potrebbe assumere valori maggiori che in m. Analogamente si dice che ha la funzione ha un minimmo relativo in m se ivi assume il valore minimo rispetto ad un intervallo centrato in tale valore. Se si vuole evidenziare che un tale punto, oltre ad essere di minimo o di massimo relativo, è un massimo o minimo nell'intero dominio della funzione, si parla anche di massimo o di minimo assoluto.  I problemi di ricerca del massimo o del minimo di una funzione sono chiamati anche problemi di ottimizzazione e, per le applicazioni che hanno in ambito economico e tecnologico, sono uno dei settori della matematica applicata più usati.     In modo analogo posso determinare i vertici delle parabole, con un procedimento più semplice di quello algebrico ( funz. polinomiali):  il vertice di  y = 4x2 + 12x – 1  ha x tale che Dx(4x2+12x–1)=0, ossia 8x+12=0, ossia x=-3/2; la y del vertice è 9–18–1 = -10; il vertice è (-3/2,-10).   Nel caso di una generica parabola  y = ax2 + bx + c  ho:  Dx(ax2+bx+c) = 2ax+b = 0 per x = –b/(2a). Esercizio:  testo e soluzione   Infine, la derivata consente di esprimere la velocità di variazione di una grandezza.     Pensiamo al caso in cui P(t) sia la posizione lungo una autostrada in cui si trova all'ora t un mezzo che viaggia a velocità costante. In questo caso P(t) varia proporzionalmente alla variazione di t:  se raddoppia il tempo trascorso raddoppia la strada percorsa) e ΔP(t)/Δt, ossia il rapporto tra la strada percorsa e il tempo impiegato, esprime la velocità del mezzo.  Ad es., se la posizione è espressa chilometricamente e il tempo in ore, ΔP(t)/Δt = 115 indica che il mezzo viaggia a 115 km/h.     Se il mezzo non ha velocità costante possiamo approssimare la velocità che ha all'istante t calcolando ΔP(t)/Δt per una piccola variazione di tempo.  Ad esempio se per Δt = 1/60, ossia al passare di 1 min, la posizione lungo la strada ha subito la variazione ΔP(t) = 2, allora ΔP(t)/Δt = 120: il mezzo viaggia a circa 120 km/h; questa sarebbe esattamente la sua velocità se in questo intervallo di tempo non avesse accelerato o decelerato.     La velocità all'istante t non è altro che limΔt→0ΔP(t)/Δt, ossia P'(t).     Questa formula non è altro che la sintesi del procedimento che puoi trovare sviluppato più estesamente alla voce  velocità di variazione.     Potremmo anche ragionare in termini di variazione tendenziale, come fatto all'inizio di questa voce: la velocità all'istante t non è altro che il rapporto tra la variazione tendenziale dP(t) della posizione lungo la strada del mezzo (di quanto si sposterebbe se mantenesse la stessa andatura) e la variazione Δt del tempo, che non è altro che P'(t). 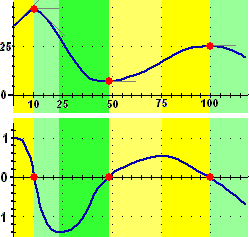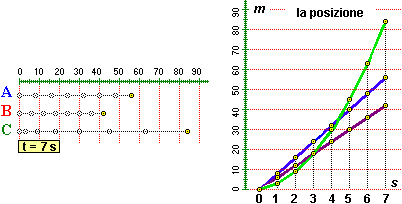•  Vediamo, in breve, un esempio discusso alla voce  velocità di variazione. Tre mezzi avanzano nel modo raffigurato sotto a sinistra, mediante foto scattate ad intervalli di 1 secondo. A destra la loro posizione x (in m) in funzione del tempo t (in s) è descritta anche mediante formule. A e B hanno velocità costante, C sta accelerando, ossia ha velocità crescente. Per quanto ora visto, le loro velocità (in m/s) sono: vA(t) = D(6t) = 6 vB(t) = D(8t) = 8 vC(t) = D(1.5t2 + 1.5t) = 3t + 1.5     Geometricamente, nei primi due casi 6 e 8 corrispondono alla pendenza costante dei grafici di x in funzione di t, nel terzo caso 3t+1.5 indica come varia la pendenza al trascorrere del tempo.     Per valutare come varia la velocità di C al passare del tempo possiamo a sua volta derivare vC(t): accelerazione di C  =  Dt(vC(t))  =  Dt(3t + 1.5)  =  3 Il mezzo C sta avanzando con accelerazione costante: la sua velocità aumenta di 3 m/s ogni secondo, ossia di 3 m/s/s = 3 m/s2. •  Un esempio in cui la velocità di variazione non è rispetto al tempo: qual è la velocità con cui cresce il volume V di un cubo al crescere del lato l? e l'accelerazione?   V  =  l 3;   d V / d l  =  3 l 2: velocità;   d 3 l 2 / d l  =  6 l : accelerazione (anche l'accelerazione in questo caso è crescente).   Galileo - I vettori velocità e accelerazione (e forza)   [← clicca]   L'area della matematica che si occupa dello studio delle proprietà e delle applicazioni del concetto di derivata si chiama calcolo differenziale.  L'area più generale che si occupa delle funzioni a (uno o più) input e output reali (o  complessi), del concetto di limite e degli altri concetti ad esso collegati (oltre alle derivate, i metodi per calcolare lunghezze, aree e volumi di figure definite mediante funzioni od equazioni, le proprietà delle funzioni continue, …) viene chiamata analisi matematica.  Spesso l'aggettivo analitico, in matematica, viene usato per indicare metodi in cui un oggetto o una proprietà viene studiata usando tecniche di analisi matematica. In particolare lo studio delle figure mediante il ricorso alle funzioni od equazioni che le hanno per grafici viene a volte chiamato geometria analitica (è una terminologia introdotta nei primi anni del XIX secolo per distinguerla dall'approccio alla geometria allora più diffuso, in cui lo studio delle figure era basato su metodi, più direttamente legati alla immediata intuizione fisica, che non ricorrevano ai numeri reali e alle funzioni). Altri esercizi:   testo   e   soluzione;    testo   e   soluzione;    testo   e   soluzione.