Equazioni differenziali - 1

    Abbiamo visto come, data una funzione, se ne può studiare la variazione utilizzando le sue derivate prima, seconda, ….  Qui vedremo, viceversa, che da informazioni su come varia una funzione si possono dedurre informazioni sulla funzione stessa.

  Esempi

Suppongo di sapere che un corpo A si muove alla velocità costante di 8 m/s e che un corpo B si muove alla velocità crescente di (3 t + 1.5) m/s, dove t è il tempo espresso in secondi dall'istante t = 0 in cui l'oggetto è partito.  Sto ipotizzando, per semplicità, che un corpo possa partire immediatamente a tale velocità; in realtà sappiamo che la potrà raggiungere solo dopo qualche istante

    Se indico con x_A e con x_B la strada in metri percorsa dai due oggetti dopo t secondi, posso scrivere:

d xA / d t = 8 d xB / d t = 3 t + 1.5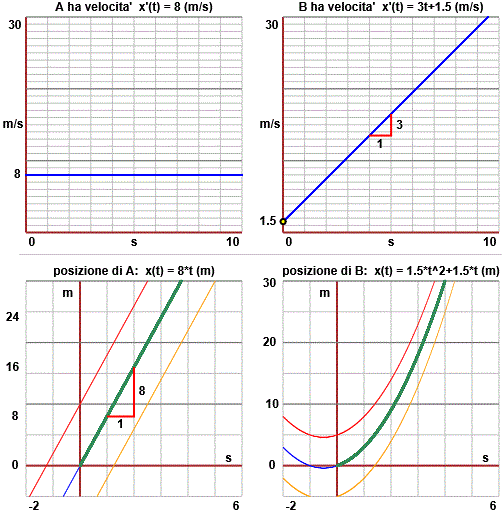
Posso ricavare:   xA = 8 t   (grafico verde)   ma anche:   xA = 8 t + 10,  xA = 8 t − 10, … e:   xB = 1.5 t2 + 1.5 t   (grafico verde)   ma anche:     xB = 1.5 t2 + 1.5 t + 10,     xB = 1.5 t2 + 1.5 t − 10, …

Abbiamo tracciato anche i tratti corrispondenti a  t < 0, in quanto, in entrambi i casi, avremmo potuto considerare un istante precedente a  t = 0.  Le "soluzioni", ossia le equazioni che esprimono x_A e x_B in funzione di t, sono in entrambi i casi infinite:  solo se fisso la posizione in un istante fissato, ad es. per t = 0, posso individuare una particolare soluzione.

Equazioni come queste  [x'(t) = 8,  x'(t) = 3t+1.5]  che ci forniscono delle informazioni sulla derivata di una funzione incognita  [x(t) in questi casi]  vengono chiamate equazioni differenziali.  Ne vedremo vari altri esempi.

Si usano spesso dei diagrammi per schizzare l'insieme delle le soluzioni di un'equazione differenziale realizzati prendendo dei punti del piano e tracciando segmentini centrati in essi aventi la pendenza indicata dalla equazione. Ad esempio nel secondo caso tracciando dei segmentini in punti (t,x) aventi pendenza 3t+1.5. Questi diagrammi vengono chiamati campi direzionali o campi vettoriali  ("vector field" in inglese, comando usabile col software online WolframAlpha)  in quanto i segmenti indicano la direzione delle curve-soluzione. Si capisce bene dalla figura di che tipo devono essere le soluzioni. Il tracciamento del campi direzionali è utile per controllare le soluzioni o per instradare alla ricerca di esse.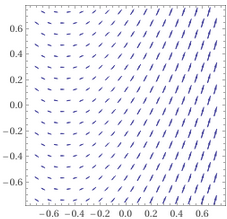

  Se so che la derivata prima di g è x → |x|  ( g '(x) = |x|; qui, a differenza che nell'esempio precedente, ho indicato con x la variabile indipendente), che cosa posso dire di g ?

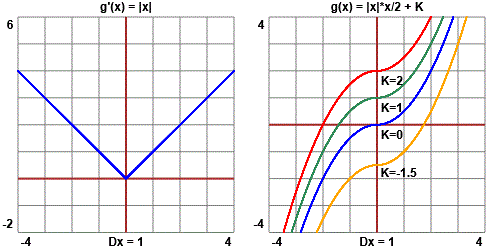
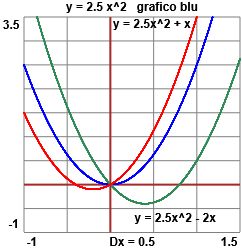
Per x ≥ 0  g '(x) = x:  quindi  g(x) = x²/2.   Per x ≤ 0  g '(x) = −x:  quindi  g(x) = −x²/2.  Posso riassumere tutto con:  g(x) = x · |x| / 2.

    Ma il "quindi" non è corretto:  anche  g(x) = x · |x| / 2 + 1,  g(x) = x · |x| / 2 + 2,  g(x) = x · |x| / 2 − 2, … soddisfano l'equazione di partenza,  g '(x) = |x|.

    Sopra, al centro, sono state tracciati i grafici di alcune funzioni che verificano l'equazione di partenza, ed è evidenziato come esse differiscano per una costante.  A destra è riprodotto il campo direzionale ottenuto con WolframAlpha col comando "vector field dy/dx = |x|".

  Equazioni (e modelli) differenziali

Gli esempi visti nei due paragrafi precedenti possono essere riassunti nel modo seguente, in cui abbiamo indicato con f la funzione incognita, con x la variabile indipendente, e con c una qualunque costante:
      f '(x) = 8,  f(x) = 8x + c       f '(x) = 3x + 1.5,  f(x) = 1.5x² + 1.5x + c       f '(x) = |x|,  f(x) = x·|x|/2 + c

In tutti e tre i casi abbiamo che l'equazione considerata  f '(x) = ...  ha infinite soluzioni:
      f(x) = 8x + 10,  f(x) = 8x,  f(x) = 8x − 10,  ... sono soluzioni di   f '(x) = 8,
      f(x) = 1.5x² + 1.5x + 10,  f(x) = 1.5x² + 1.5x,  f(x) = 1.5x² + 1.5x − 10,  ... sono soluzioni di   f '(x) = 3x + 1.5,
      f(x) = x · |x| / 2 + 1,  f(x) = x · |x| / 2 ,  f(x) = x · |x| / 2 − 2  ... sono soluzioni di   f '(x) = |x|.

L'equazione  f '(x) = ... , equazione differenziale nell'incognita f(x), come abbiamo visto, ha infinite soluzioni  f(x) = ... + c, una per ogni valore di c, che corrispondono a grafici paralleli, ottenibili uno dall'altro mediante una traslazione verticale.

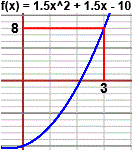
Se fissiamo un punto (x0, y0) per cui deve passare il grafico otteniamo una sola funzione (a patto, naturalmente, che x0 stia nel dominio di f ' e che questo sia un intervallo).  In questo caso si usa dire che la funzione trovata è una soluzione del  modello differenziale  "f '(x) = ...  e  f(x0) = y0".  Ad esempio di fronte a  f '(x) = 3x + 1.5  e alla richiesta che f(3) = 8 ottengo: f(x) = 1.5x2 + 1.5x + c  AND  f(3) = 8; 8 = 1.5·9 + 1.5·3 + c;       c = 8 − 18 = −10; f(x) = 1.5x2 + 1.5x − 10   (vedi figura a fianco).     Con WolframAlpha con "solve f '(x) = 3x + 1.5, f(3)=8" ottengo: "f(x) = 1.5 x^2 + 1.5 x - 10".

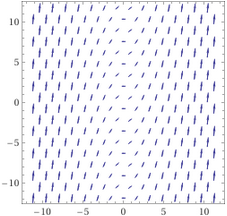
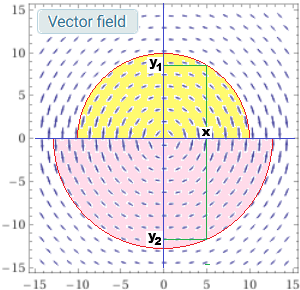
Se l'equazione, però, contiene la funzione incognita anche senza il simbolo di derivata, come nell'esempio seguente:         f '(x) = − x / f(x) in genere scritto così (indicando la funzione incognita con y):         y'(x) = − x / y(x) l'equazione non ha necessariamente soluzioni corrispondenti tutte a grafici paralleli: come si vede a destra, in cui sono tracciati tanti trattini con pendenza -x/y, nel caso considerato la pendenza y' a una curva soluzione deve essere perpendicolare al segmento che congiunge l'origine con (x, y)  (vedi figure 2), e quindi le soluzioni dell'equazione hanno tutte come grafico dei mezzi cerchi con centro nell'origine, rivolti verso il basso (nel caso in cui la curva debba passare per (x0,y0) con y0 > 0) o rivolti verso l'alto (nel caso in cui la curva debba passare per (x0,y0) con y0 < 0):  nella figura a lato, per lo stesso x0, sono state tracciate due soluzioni una avente ordinata y0 positiva, una avente ordinata y0 negativa.     Il campo direzionale è stato tracciato con WolframAlpha mediante il comando "vector field dy/dx = -x/y", che ci fornisce anche le soluzioni.

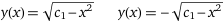  Alla voce  derivata e differenziale abbiamo visto vari altri esempi di funzioni dallo studio della cui derivata (dove cresce o decresce, dove si annulla, ...) possiamo dedurre informazioni relative alla funzione di partenza. In ogni caso, noto il valore di f ' e fissata una coppia (x₀, y₀), possiamo ricavare un'unica funzione f tale che f ' = ..., che è definita in un intervallo contenente x₀ e tale che f(x₀) = y₀.

Se, invece, avessimo un problema del tipo  f "(x) = ...  dove f " indica la derivata della derivata di f, fissata (x0, y0) potremmo avere più soluzioni f tali che f(x0) = y0.     Se ad esempio avessimo  f "(x) = 5, avremmo che  f '(x) = 5x + h  e, quindi,  f(x) = 2.5x2 + h·x + k  verifica l'equazione iniziale, qualunque siano i valori di h e di k.  A destra sono raffigurate tre tra le infinite funzioni f che risolvono f "(x) = 5 e sono tali che f(0) = 0.     Si vedrà in una successiva voce che potrà ottenersi un'unica soluzione che soddisfa l'equazione  f "(x) = ...  se si imporrà un'ulteriore condizione:  qual è il valore che assume f '(x0).     Qui limitiamoci a un esempio che fa riferimento ad un contesto noto.     Consideriamo il caso in cui  s"(t) = 5  sia l'accelerazione costante in m/s2 di un'automobile che all'istante t = 0 (t espresso in secondi) sia nella posizione s = 0 (s in metri).

    Sono infinite le curve che potrebbero descrivere il moto della nostra automobile:
                s(t) = 2.5·t² + h·t + k, da cui,  dato che s(0) = 0,  k = 0.
    Ad esempio:  s(t) = 2.5 t² + t, s(t) = 2.5 t², s(t) = 2.5 t² − 2t, …  hanno  s'(t) = 5 t + 1, s'(t) = 5 t, s'(t) = 5 t − 2, …  e, tutte, s"(t) = 5, oltre a  s(0) = 0.

    s'(t) = 2.5·2·t + h.  Se imponiamo che  s'(0) = 0  ricaviamo  h = 0, quindi  s(t) = 2.5 t².
    Con WolframAlpha: s"(t) = 5, s(0) = 0, s'(0) = 0  →  s(t) = 5t²/2.

    Se imponiamo, per esempio, che s'(0) = 1 (1 m/s = 3.6 km/h), ricaviamo h = 1, da cui  s(t) = 2.5 t² + t.
    Con WolframAlpha: s"(t) = 5, s(0) = 0, s'(0) = 0  →  s(t) = 5t²/2 + t

  Per esempi che coinvolgono le funzioni circolari vedi la successiva voce Funzioni circolari e trigonometria.   Per approfondimenti sulle equazioni differenziali affrontabili alla fine delle scuole superiori vedi la scheda Modelli differenziali  (vedi qui le altre schede).