Figure 1
 Abbiamo richiamato dalla scuola di base i principali concetti
geometrici nella voce
Abbiamo richiamato dalla scuola di base i principali concetti
geometrici nella voce  prime figure e nei relativi esercizi, oltre che negli esercizi relativi a varie altre voci (e in particolare nelle voci "proporzionalità", "diagrammi", "lo spazio", "distanza").
prime figure e nei relativi esercizi, oltre che negli esercizi relativi a varie altre voci (e in particolare nelle voci "proporzionalità", "diagrammi", "lo spazio", "distanza").
Qui incominciamo ad approfondire il concetto di figura geometrica..
Con figura intendiamo un insieme di punti in un dato spazio. Ad esempio nello spazio "retta numerica" presi due punti-numeri a e b, possiamo considerare il segmento costituito dai punti x tali che a ≤ x ≤ b (si veda la figura sotto a sinistra).
Possiamo rendere compatta la descrizione di molte figure abbreviando "l'insieme degli α tali che sia vera la
condizione Γ" con:
{ α t.c. Γ } o { α : Γ } o { α / Γ } o { α | Γ }
Ecco tre semplici esempi di figure riferiti agli spazi numerici a 1, 2 e 3
dimensioni:
| {x : a ≤ x ≤ b} |
{(x,y) : a ≤ x ≤ b AND c ≤ y ≤ d} |
 |
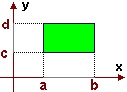 |
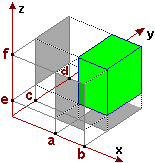 |
{(x,y,z) : a ≤ x ≤ b AND c ≤ y ≤ d AND e ≤ z ≤ f} |
Qualche altro esempio riferito al caso bidimensionale (qui d è la distanza euclidea):
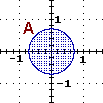 | 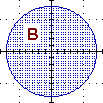 | 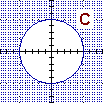 |  |  |
{(x,y) : x2+y2 ≤ 1/2}
ossia:
{P : d(P,O) ≤ √(1/2)} |
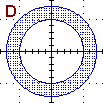
{(x,y) : x2+y2 ≤ 2}
ossia:
{P : d(P,O) ≤ √2} |
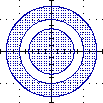
{(x,y) : 1 ≤ x2+y2}
ossia:
{P : 1 ≤ d(P,O)} |
{(x,y) : 1 ≤ x2+y2 ≤ 2}
intersezione
tra B e C |
{(x,y) : 1 ≤ x2+y2 ≤ 2
OR x2+y2 ≤ 1/2}
unione di A e D |
Nota. A volte si sottointende {(…) : …} e si scrive semplicemente la condizione. Ad esempio per indicare la retta del piano costituita dai punti di ascissa 1 invece di {(x,y) : x=1} si scrive "la retta x=1" o "la retta di equazione x=1".
 Soffermiamoci sul caso bidimensionale, cioè sul piano cartesiano [
Soffermiamoci sul caso bidimensionale, cioè sul piano cartesiano [ ].
].
La figura  al centro nell'illustrazione iniziale è un
rettangolo; facendo variare a, b, c e d otteniamo tutti i rettangoli con lati paralleli agli assi.
al centro nell'illustrazione iniziale è un
rettangolo; facendo variare a, b, c e d otteniamo tutti i rettangoli con lati paralleli agli assi.
Per dare una
definizione puramente matematica che comprenda anche i rettangoli
con lati non paralleli agli assi, che si possono ottenere da
figure come questa mediante una rotazione, occorre disporre prima di una definizione
matematica del concetto di rotazione o del concetto di perpendicolarità ( figure2).
figure2).
|
 Per ora siamo in grado solo di traslare figure
[ Per ora siamo in grado solo di traslare figure
[ vettori]. vettori].
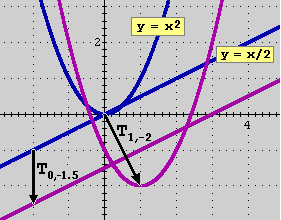
A fianco, ad esempio, sono rappresentate:
• la figura costituita
dai punti del grafico della funzione x → x/2 con la figura che si ottiene da essa mediante la traslazione
con passi Δx = 0, Δy = –1.5,
• e il grafico della
funzione x → x2 con la figura ottenuta traslando questo con passi Δx = 1,
Δy = –2.
|
|
|
 A fianco sono rappresentate le figure costituite dai punti che
distano 10 dall'origine rispettivamente secondo la distanza
euclidea e secondo la distanza urbanistica ( A fianco sono rappresentate le figure costituite dai punti che
distano 10 dall'origine rispettivamente secondo la distanza
euclidea e secondo la distanza urbanistica ( piano), cioè: piano), cioè:
{ (x,y) : x2 + y2 = 100 } e
{ (x,y) : |x| + |y| = 10 }
Nota. √(x2+y2) = 10 equivale a x2+y2 = 100 poiché 0 ≤ x2+y2
|
|
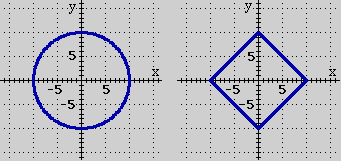
Nell'ambito della geometria piana euclidea, cioè dello studio delle figure del piano cartesiano dotato della distanza euclidea, la figura a sinistra è il cerchio di centro (0,0) e
raggio 10.
La figura a destra è un quadrato. Per dare una definizione generale di quadrato occorre far riferimento ad ulteriori concetti (vedi quanto osservato sopra a proposito dei rettangoli). Qui ci limitiamo a osservare che le distanze da un
vertice al successivo, ad esempio dal punto (0,10) al punto (10,0),
sono tutte uguali a √(102+102) = √200 e che le diagonali, cioè le distanze da
un vertice al vertice opposto, sono tutte uguali a 20.
Nota. La figura soprastante a destra (nella geometria euclidea)
è un quadrato. È anche un rombo,
come ogni quadrato, ma, appunto, non è solo un rombo: un quadrato non ha necessariamente i lati orizzonali
e verticali.
 Se non avessimo scelto un sistema monometrico [
Se non avessimo scelto un sistema monometrico [ pendenza] avremmo
potuto ottenere le rappresentazioni seguenti.
pendenza] avremmo
potuto ottenere le rappresentazioni seguenti.
|
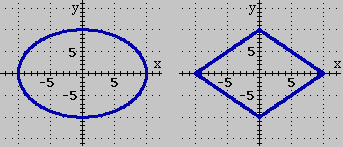
L'aspetto non è più quello di un "cerchio"
o di un "quadrato": se misuriamo "fisicamente" le
distanze con un righello, i punti della figura a sinistra non hanno
la stessa distanza dal punto (0,0) e le due diagonali della seconda
figura non hanno la stessa lunghezza.
|
|
Ma dal punto di vista "matematico", riferendosi al piano
cartesiano e alla distanza euclidea, siamo solo di fronte a una
diversa rappresentazione concreta delle stesse figure. Quindi, ad
esempio, la figura disegnata a sinistra è un "cerchio".
Abbiamo già fatto una analoga distinzione tra la  pendenza "stradale" e quella "dei grafici".
pendenza "stradale" e quella "dei grafici".
 Nota. Per rappresentare graficamente figure descritte mediante
equazioni, come le due figure precedenti, posso ricorrere a programmi in grado di rappresentare equazioni del tipo
E(x,y)=0, come, appunto, x2+y2–100=0 e
|x|+|y|–10=0 (con WolframAlpha
basta introdurre x^2+y^2-10=0 e |x|+|y|-10=0).
Nota. Per rappresentare graficamente figure descritte mediante
equazioni, come le due figure precedenti, posso ricorrere a programmi in grado di rappresentare equazioni del tipo
E(x,y)=0, come, appunto, x2+y2–100=0 e
|x|+|y|–10=0 (con WolframAlpha
basta introdurre x^2+y^2-10=0 e |x|+|y|-10=0).
Posso provare a realizzare tali figure anche mediante il tracciamento di grafici di funzioni. Devo, però, trasformare l'equazione in una equazione o in
più equazioni del tipo y=…, cioè risolvere
l'equazione rispetto a y.
Nei nostri casi abbiamo che:
| x2 + y2 – 100 = 0 |
equivale a |
y = √(100 – x2)
OR
y = –√(100 – x2) |
|
|
|x| + |y| – 10 = 0 |
equivale a |
(y = 10 – |x| AND –10 ≤ x ≤ 10) OR
(y = – (10 – |x|) AND –10 ≤ x ≤ 10) |
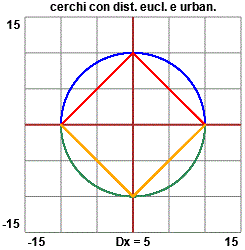 |
Vedi qui lo script con cui è stato realizzato il grafico.
Esercizi:
uno, sol.,
due, sol.,
tre, sol.,
quattro, sol.
cinque, sol.,
sei, sol.,
sette, sol.,
otto, sol.,
nove, sol.
Altri esercizi per la scuola di base
 Abbiamo richiamato dalla scuola di base i principali concetti
geometrici nella voce
Abbiamo richiamato dalla scuola di base i principali concetti
geometrici nella voce  prime figure e nei relativi esercizi, oltre che negli esercizi relativi a varie altre voci (e in particolare nelle voci "proporzionalità", "diagrammi", "lo spazio", "distanza").
prime figure e nei relativi esercizi, oltre che negli esercizi relativi a varie altre voci (e in particolare nelle voci "proporzionalità", "diagrammi", "lo spazio", "distanza").











