 Il valor medio
Il valor medio
| Se conosco come varia la velocità v di un'automobile in un intervallo di tempo [a,b], che cosa intendo per velocità media: la velocità costante a cui sarebbe andata per percorrere la strada nello stesso tempo. Quindi il suo valore lo trovo dividendo la strada percorsa per il tempo impiegato. | ||||
La strada percorsa, ossia la differenza  integrazione] integrazione]Quindi: velocità media = ∫[a,b] v(t) dt / (b-a). Passando da v a una generica funzione f continua positiva su [a,b], definiamo come valore medio di f in [a,b] l'altezza m del rettangolo di base [a,b] avente area uguale a quella compresa tra il grafico di f e l'intervallo [a,b]. Più in generale, se f è una qualunque funzione integrabile su [a,b], definiamo come valore medio di f in [a,b] il valore della funzione costante che ha su [a,b] lo stesso integrale, ossia: | 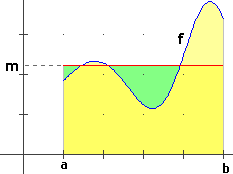 | |||
| ||||
Si ha, facilmente, che vale un teorema del valor medio per gli integrali:
se f è continua su [a,b], esiste c in [a,b] in cui f assume il valore medio, ossia tale che:
f(c) =
∫[a,b] f / (b-a).
Nel caso della figura soprastante, vi sono tre di tali c: le ascisse dei punti in cui il grafico di f taglia la retta di ordinata m.
Il teorema del valor medio per le derivate
( propr. delle funzioni cont. e di quelle derivabili)
propr. delle funzioni cont. e di quelle derivabili)
Il secondo degli esercizi seguenti illustra come si possa ricorrere a queste idee per determinare il centro di
massa di un oggetto piano di spessore costante.
Esercizio 1 (e soluzione) Esercizio 2 (e soluzione)
Generalizziamo alcuni metodi già visti
( il volume)
per individuare il volume di una figura tridimensionale. Il particolare ci occuperemo
delle figure che possono essere generate mediante la rotazione attorno ad un asse
di una figura piana. Illustriamo le
"tecniche" impiegabili partendo da un caso in cui sappiamo determinare il volume
anche con altri metodi.
il volume)
per individuare il volume di una figura tridimensionale. Il particolare ci occuperemo
delle figure che possono essere generate mediante la rotazione attorno ad un asse
di una figura piana. Illustriamo le
"tecniche" impiegabili partendo da un caso in cui sappiamo determinare il volume
anche con altri metodi.
| •
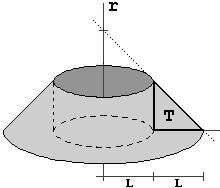
Determino il volume del solido raffigurato a lato, dotato di un asse di simmetria,
con la superficie "interna" cilinidrica di raggio uguale all'altezza, una faccia a forma di corona circolare
e il resto della superficie a profilo rettilineo, inclinato di 45° rispetto all'asse di simmetria
(i semipiani aventi come bordo l'asse di simmetria intercettano sul solido dei triangoli rettangoli isosceli).
L (la lunghezza dei cateti del triangolo T) è sia lo spessore della corona circolare che l'altezza e
il raggio del cilindro. Suppongo che L = 1, ossia uso come unità di volume L3. Posso pensare il solido come un cono circolare retto di altezza e raggio 2 da cui ho tolto un cono di altezza e raggio 1 e un cilindro circolare retto di altezza e raggio 1. Ottengo: |
 |
 | •
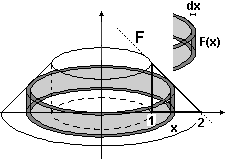
Ora ricavo il volume usando direttamente
qualche tecnica di integrazione. Dovrei ottenere lo stesso risultato. Penso il solido come frutto della rotazione di una figura attorno all'asse di simmetria. Nel mio caso posso pensare il profilo della figura − sia come grafico di una funzione F assumendo l'asse di rotazione come asse y − che come quello di una funzione G assumendo l'asse di di rotazione come asse x. |
 |
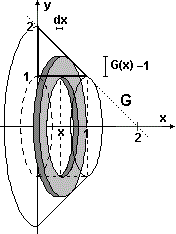
| Col secondo metodo (figura a sinistra) penso il solido come somma di tanti anelli (rondelle) di spessore Δx, raggio esterno G(x) e interno 1: | ||
| la variazione ΔV del volume al passare da x a x+Δx
è approssimabile con π(G(x)2-1) (area della corona circolare base dell'anello)
per Δx: dV = | ||
|
Col primo metodo (figura a destra) penso il solido come somma di cilindretti cavi (gusci cilindrici)
di spessore Δx, raggio interno x e altezza la variazione ΔV del volume al passare da x a x+Δx è approssimabile con | ||
Il calcolo lo potrei fare facilmente anche con lo script "integrali" presente qui
 Vediamo altri due esempi.
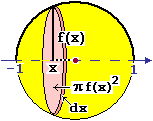
Determiniamo il volume di una sfera in modo alternativo
rispetto a quanto già visto
(
Vediamo altri due esempi.
Determiniamo il volume di una sfera in modo alternativo
rispetto a quanto già visto
( il volume) il volume)∫[−1, 1] π f(x)2 dx = ∫[−1, 1] π(1−x2)dx = In pratica, questo metodo dei dischi non è che un caso particolare del metodo delle rondelle. |
 |
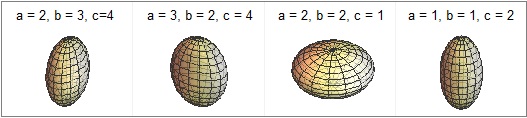
Osserviamo che, in modo simile, si pu dimostrare che, pi in generale, l'area dell'elissoide (x/a)²+(y/b)²+(z/c)² = 1
è
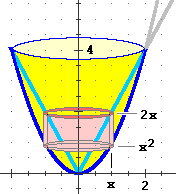 |
Vediamo, ora, come ottenere il volume del solido a fianco
(una specie di bicchiere),
ottenuto ruotando attorno all'asse y la regione compresa
tra y = 2x e y = x2 per x in
Potrei procedere come sopra, pensando il solido affettato orizzontalmente,
come composto da tante rondelle. Procediamo, invece, pensandolo come composto
da tanti gusci cilindrici di raggio x, altezza Il calcolo lo potrei fare facilmente anche con lo script "integrali": |
Un solido di rotazione diffuso è la botte. Se il profilo è parabolico, se D e d sono il diametro massimo e il diametro minimo (interni) ed h è l'altezza (interna), la capacità della botte è la seguente (come controllo, si noti che se d = D si ritrova il volume del cilindro):
π·h·(3·d² + 4·d·D + 8·D²) / 60 | 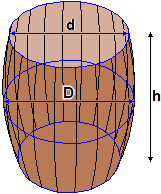 |
Abbiamo già visto ( lunghezza)
come valutare la lunghezza del grafico di una funzione f continua definita su un intervallo chiuso e limitato lunghezza)
come valutare la lunghezza del grafico di una funzione f continua definita su un intervallo chiuso e limitato Lo stesso algortimo (vedi qui) può essere utilizzato per trovare la lunghezza di generiche curve. Vediamo per esempio come calcolare la lunghezza dell'ellisse raffigurata a fianco: a=0; b=2*Math.PI document.write("la lunghezza della curva da t="+a+" a t="+b+"<br>") function x(t) {return Math.cos(t)} function y(t) {return Math.sin(t)/Math.sqrt(2)} n = 1e5; rip=6 for(k=1; k<=rip; k=k+1) { n=n*2; e=(b-a)/n; L=0 for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e L=L+Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))} document.write("n = "+n+", L = "+L+"<br>") } Otteniamo: | 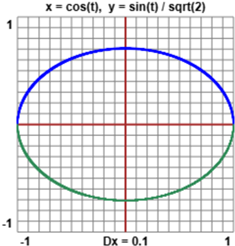 |
la lunghezza della curva da t=0 a t=6.283185307179586
n = 200000, L = 5.402575523968448
n = 400000, L = 5.40257552413516
n = 800000, L = 5.402575524177035
n = 1600000, L = 5.402575524187061
n = 3200000, L = 5.402575524189719
n = 6400000, L = 5.402575524190111
concludendo che la lunghezza arrotondata è 5.40257552419.
Il valore esatto sarebbe 5.402575524190702010080698941354903...
(calcolabile con WolframAlpha col comando
int 4*sqrt( 1-sin(x)^2/2 ), x=0..PI/2 )
Si può calcolare la lunghezza con un procedimento non sperimentale? In alcuni casi sì. Qui sotto è spiegato come farlo in un caso particolare.
Siano f e g derivabili in [a, b], nel senso che ne esistano la derivata in (a, b) e le derivate sinistra e destra in a e in b.
Suddivido [a, b] in n sottointervalli di eguale ampiezza [t0, t1], [t1, t2], …, [tn-1, tn] dove a = t0 < t1 < … < tn-1 < tn = a.
Siano xi e yi le coordinate dei punti corrispondenti.
La poligonale che ne risulta approssima il nostro arco di curva.
Ecco una traccia di come ottenere una formula per il calcolo della lunghezza dell'arco:
x = f(t), y = g(t)
∫ [a, b] | 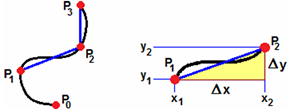 |
Nel caso particolare in cui la curva sia il grafico di una funzione f la formula precedente si riduce ad essere:
∫ [a, b]
la lunghezza della curva da t=0 a t=1 n = 200000, L = 1.4397098733637652 n = 400000, L = 1.4397098733695197 n = 800000, L = 1.4397098733710114 n = 1600000, L = 1.4397098733713714 n = 3200000, L = 1.4397098733714764 n = 6400000, L = 1.439709873371569 arrotondando 1.439709873372
Esercizio 1 (e soluzione) Esercizio 2 (e soluzione)
 Calcolo dei momenti di inerzia
Calcolo dei momenti di inerzia
Vai qui per l'uso dell'integrazione per
calcolare il  momento di inerzia (e il centroide) di vari corpi.
momento di inerzia (e il centroide) di vari corpi.