I limiti in probabilità [1ª parte] (2ª)
|
 Esempi introduttivi Esempi introduttivi
| | 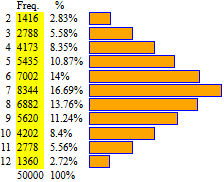 |
Primi esempi. Abbiamo visto che generando molte volte la somma delle uscite di due dadi bilanciati questa si distribuisce in modo simmetrico, formando una specie di triangolo.
Abbiamo visto che se considero la somma di più di due dadi bilanciati e ne genero molte uscite,
l'istogramma tende ad avere una forma "a campana". Sotto il caso di 300 lanci e 50 000 lanci di
quattro dadi bilanciati.
 | |
Ma anche se lancio un dado non equo come quello in cartoncino disegnato a fianco
( leggi di distribuzione - var. discrete), se passo dall'esito della ripetizione molte volte del lancio di due dadi a quello del lancio di quattro, ho che l'istogramma tende ad avere una forma a "campana".
Vedi i successivi istogrammi (dadi(4)non bilanciati). leggi di distribuzione - var. discrete), se passo dall'esito della ripetizione molte volte del lancio di due dadi a quello del lancio di quattro, ho che l'istogramma tende ad avere una forma a "campana".
Vedi i successivi istogrammi (dadi(4)non bilanciati). |
|
4 dadi bilanciati:
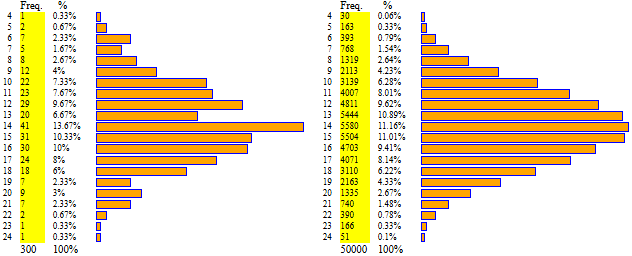
4 dadi non bilanciati:
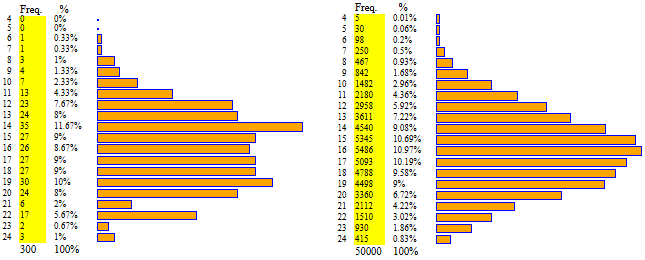
Abbiamo visto
( leggi di distribuzione - var. discrete)
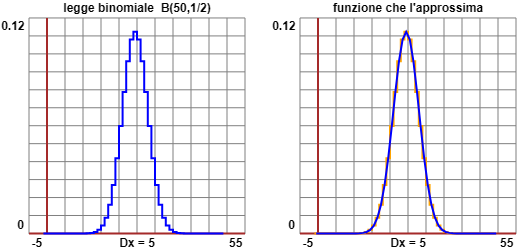
che anche il grafico della legge binomiale Bn,p
(di ordine n e "probabilità di successo nella singola prova" p) quando n cresce
tende ad assumere una forma simile.
leggi di distribuzione - var. discrete)
che anche il grafico della legge binomiale Bn,p
(di ordine n e "probabilità di successo nella singola prova" p) quando n cresce
tende ad assumere una forma simile.
Altro esempio. Con un apparato misuratore ad alta sensibilità si ottengono le 7 misure (in un'opportuna unità di misura): 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4. Come faccio a determinare, con una certa precisione, il "valore vero" della misura?
Proviamo ad utilizzare "calcolatrice2" presente qui (come abbiamo già fatto in precedenza, nelle due voci "leggi di distribuzione", qui e qui).

n = 7 mean = 7.2 variance = 0.022857142857141355
scarto quad. medio (sq.root of var./theoret.st.dev.) = 0.15118578920368592
experimental standard dev. = 0.16329931618553986
sigma = 0.06172133998483474 3*sigma = 0.1851640199545042
A parte il chiaro significato della media, dobbiamo interpretare i valori della varianza e dello scarto quadratico medio, oltre a interpretare le ultime uscite:
prima avevamo a che fare con migliaia di prove che praticamente ci consentivano di trarre conclusioni sull'intera popolazione,
qui, invece, abbiamo a che fare con poche prove da cui vogliamo dedurre valutazioni sull'intera popolazione. Chiariremo tutto tra poco.
Nota.
Vengono spesso usati i termini statistica descrittiva e statistica
induttiva (o statistica inferenziale) per indicare, rispettivamente, la parte della matematica
che si occupa della raccolta e della descrizione di una serie di dati su certi fenomeni e quella che si occupa
della rappresentazione dei fenomeni stessi mediante dei modelli matematici che cercano di descriverne il comportamento
nel caso astratto, in cui si diponesse di tutti i dati raccoglibili, ovvero che cercano di studiarli attraverso una simulazione. La statistica inferenziale, dunque,
mette insieme gli stumenti utilizzati dalla statistica descrittiva con quelli messi a punto per affrontare il
calcolo delle probabilità. Questo collegamento tra i dati osservati e la loro rappresentazione
mediante opportuni modelli matematici astratti è l'oggetto di studio di questa voce degli Oggetti Matematici.
 Il teorema limite centrale
Il teorema limite centrale
Le prime osservazioni fatte nel paragrafo precedente
possono essere precisate, ricordando che curve a campana simili a quelle ivi riportate
sono i grafici delle distribuzioni chiamate gaussiane (o normali):  leggi di distribuzione - var. continue. Rileggi, prima di andare avanti, quanto scritto nella voce sopra richiamata.
leggi di distribuzione - var. continue. Rileggi, prima di andare avanti, quanto scritto nella voce sopra richiamata.
Dunque, siano Ui (i intero positivo) delle variabili casuali (numeriche) indipendenti con la stessa legge di
distribuzione, di media m e varianza V (ovvero s.q.m. = √V). Cosa accade se le sommiamo?
Al crescere di n la variabile casuale Xn = Σ i=1..n Ui tende ad avere legge di distribuzione normale
(vedi qui se vuoi qualche precisazione)
di media m·n e varianza V·n
(vedi qui e qui)
Quindi la media delle Ui
(Σi=1..n Ui / n), ossia Xn/n,
tende ad avere distribuzione normale con media m e varianza V/n
(infatti V è espressa in una unità di misura che è il quadrato di quella dei dati e quindi devo dividere V·n per n²)
e quindi s.q.m. = √(V/n).
La proprietà descritta in questo paragrafo è nota come teorema limite centrale.
È assai importante, in quanto consente di concludere che la media di una serie di rilevamenti di una qualunque
grandezza (non i rilevamenti stessi!) ha andamento gaussiano. Nei primi esempi considerati nel paragrafo iniziale abbiamo visto che già la media
di 4 rilevamenti ha quasi tale andamento; passando da 4 a più rilevamenti questo fenomeno risulterebbe più edivente. Su ciò ritorneremo.
Del teorema limite centrale esiste anche una versione più "forte",
che si estende a situazioni in cui le variabili casuali sommate non hanno la stessa legge di distribuzione
( vedi),
e che consente di capire perché vi siano svariate grandezze di natura biologica le cui misure hanno andamento gaussiano.
vedi),
e che consente di capire perché vi siano svariate grandezze di natura biologica le cui misure hanno andamento gaussiano.
 Le proprietà della gaussiana
Le proprietà della gaussiana
Abbiamo già
messo a fuoco varie proprietà della gaussiana
( leggi di distribuzione - var. continue).
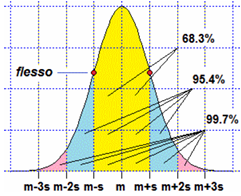
In particolare abbiamo visto che si tratta di una funzione con grafico simmetrico rispetto alla media m
che ha flessi nei punti m-s e m+s, essendo s lo scarto quadratico medio.
leggi di distribuzione - var. continue).
In particolare abbiamo visto che si tratta di una funzione con grafico simmetrico rispetto alla media m
che ha flessi nei punti m-s e m+s, essendo s lo scarto quadratico medio.
Si può dimostrare che l'integrale tra
m-h·s e m-h·s di una densità gaussiana dipende solo da h,
e non dai valori della media m e dello scarto quadratico medio s.
Ad esempio abbiamo che, per ogni m e ogni s, le
probabilità che una variabile gaussiana disti da m meno di s, 2s e 3s sono →
Con lo script gaussiana:
0.68268949234 if a=174 b=186, m=180 s=6
0.95449973539 if a=168 b=192, m=180 s=6
0.99730020394 if a=162 b=198, m=180 s=6 |
|  |
Riflettiamo, ora, sull'altro esempio. Il sigma (il nome della lettera greca σ)
indicato dallo script (0.0617) è lo s.q.m. della media dei rilevamenti, che al crescere del numero di essi si avvicina al valore "vero".
Possiamo concludere che con una probabilità di circa il 68.3% il valore vero della misura è 7.2±0.0617, o, meglio,
7.2±0.07. Invero dobbiamo fare ancora qualche considerazione: nel teorema si parla della media teorica, mentre qui abbiamo fatto i calcoli
con la media sperimentale. Preciseremo questi aspetti tra poco.
 Dalla media statistica alla media teorica
Dalla media statistica alla media teorica
Facciamo un esempio.
Voglio determinare il peso medio della popolazione adulta (di un certo paese) di un dato sesso,
ad es. maschile. Ovvero, se P è la variabile casuale "peso di un abitante adulto maschile", voglio determinare M(P).
Indico con s lo sqm di P. Rilevo i pesi P1, P2,
..., Pn di un campione di n persone, prese in modo del tutto casuale.
Σ i Pi /n (i=1..n) viene chiamata media statistica di P di ordine n; indichiamola con Mn(P). Anch'essa è una variabile casuale: a seconda degli n soggetti che considero ottengo valori leggermente diversi.
Le Pi sono
tutte variabili casuali distribuite come P; se faccio i rilevamenti in modo indipendente, per il teorema limite centrale ho che
Σ i Pi /n al crescere di n tende ad avere andamento gaussiano con media Mn(P) e scarto quadratico medio s / √n.
All'aumentare di n (possiamo dire "per n → ∞",
essendo grande la popolazione rispetto alle quantità
di rilevamenti che vengono effettuati) questo
scarto quadratico medio tende a 0, per cui il valore Mn(P) che ottengo con n
rilevamenti tende a cadere sempre più vicino a M(P).
Ad es., supponendo che P sia espressa in kg, se voglio determinare il peso medio della popolazione a meno di 0.5 kg posso fare tante prove n fino a che
s/√n < 0.5. A quel punto potrò dire che, con probabilità del 68.3%, il valore Mn(P) che ottengo approssima M(P) a meno di 0.5.
Se voglio una stima più sicura, praticamente certa,
posso fare tante prove n fino a che 3s/√n < 0.5. A quel punto potrò dire che, con probabilità del 99.7%, il valore Mn(P) trovato dista da M(P) meno di 0.5.
Quanto qui detto per P vale per ogni variabile casuale X.
Il valore di s devo già conoscerlo in base a considerazioni di qualche tipo oppure posso man mano approssimarlo sulla base degli n rilevamenti fatti: si può dimostrare (o congetturare con qualche esperimento: qui evitiamo di farlo) che, fissato n, la varianza di Mn(X), calcolata ripetutamente,
dà luogo a valori la cui media tende a Var(X)·(n-1)/n e, quindi, come s.q.m. posso prendere,
invece del valore considerato qui (spesso indicato con σn e chiamato deviazione standard teorica) il valore
seguente (spesso indicato con σn-1):
| deviazione standard sperimentale = ( |
(x1– μ)2 + (x2– μ)2 + … (xN– μ)2 | ) | 1/2 |
| ——————————————— |
| n−1 |
Spesso sia quella teorica che quella sperimentale vengono entrambe chiamate semplicemente deviazione standard.
Sta al lettore capire quale uso si sta facendo. Comunque quando n è abbastanza grande i due numeri hanno una piccola differenza relativa. Nella nostra "calcolatrice2" (presente qui) sono presenti tre tasti:

[sqm] calcola lo scarto quadratico medio o deviazione standard teorica
[sd] calcola la deviazione standard sperimentale
[sigma] calcola la sd divisa per √n, ossia lo s.q.m. della media dei dati
[3sigma] calcola il triplo di sigma
|
Torno, infine, al problema iniziale: ottenute per X le 7 misure 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4, come posso determinare il "valore vero" della media di tutti i valori di X? | |
-> mean=7.2 3*sigma=0.1851640199545042 |
| |
| 7.2 = M7(X) approssima M(X) a meno di 0.1852 con probabilità del 99.7%
|
| Si usa anche dire che [7.2-0.1852, 7.2+0.1852] è un intervallo di confidenza al 99.7% per la media di X
|
Esercizio 1 Soluzione
Nota.
Ricordiamo che sono le medie dei pesi che si misurano ad avere andamento gaussiano, non i pesi stessi. Per
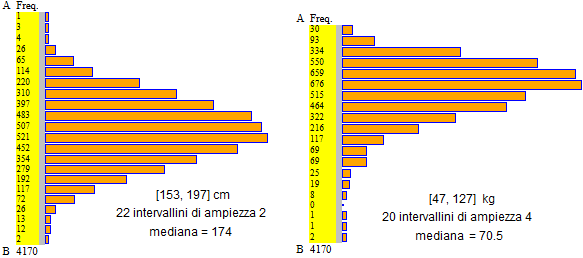
confermare questo si considerino gli istogrammi seguenti: quello a sinistra e quello a destra
rappresentano la distribuzione, rispettivamente, delle altezze (in cm)
e dei pesi (in kg) rilevati alle visite di leva per la Marina del 1997 (primi scaglioni); si tratta di circa 4 mila maschi italiani ventenni. :
Come si vede, mentre l'istogramma delle altezze ha forma approssimativamente gaussiana, ciò non vale per quello dei pesi.
Gli istogrammi sono realizzati con lo script "istogramma" presente qui (vedi gli esempi a cui si accede dallo script per recuperare i dati a cui fanno riferimento gli istogrammi).
 Convergenza in probabilità e "Legge dei grandi numeri"
Convergenza in probabilità e "Legge dei grandi numeri"
Quanto discusso ed esemplificato sopra può essere sintetizzato dicendo che
se U1, …, Un sono n variabili casuali con la stessa legge di distribuzione di media m, allora la loro media, ossia la variabile casuale
Σ i = 1…n Ui /n,
converge in probabilità a m,
ossia, fissata comunque una probabilità P, per ogni ε>0 posso trovare n tale che, da lì in poi,
Σ i = 1…n Ui /n disti da m meno di ε con probabilità P.
Il concetto di "limite in probabilità" coincide con quello usuale, a parte il fatto che si trova un
valore di n a partire dal quale vale la diseguaglianza non con certezza, ma con una certa probabilità. Ciò corrisponde al fatto che, ad es., se lancio una coppia di dadi
prima o poi la media delle uscite si stabilizza attorno a 7, ma, anche se è altamente improbabile, potrebbe accadere che a un certo punto si
susseguano 20 uscite uguali a 2 che abbassino, provvisoriamente, la media.
Le considerazioni svolte in questo paragrafo spesso sono descritte
medianti proprietà note come leggi dei grandi numeri
(e a volte raggruppate sotto la voce legge di Bernoulli
in quanto Jakob Bernoulli - intorno al 1700 - ne dette una prima formulazione).
 Possiamo a questo punto precisare
perché se si hanno dei dati approssimati alla stessa cifra (unità, decimi, …)
la loro media può essere approssimata alla cifra successiva (decimi, centesimi, …) se i dati sono almeno una decina, alla seconda cifra successiva (centesimi, millesimi, …) se sono almeno un migliaio, alla terza cifra successiva (millesimi, decimillesimi, …) se sono almeno un centinaio di migliaia, … [aggiungendo 1/2 unità corrispondente alle
cifre finali dei dati originali se questi erano troncati].
Possiamo a questo punto precisare
perché se si hanno dei dati approssimati alla stessa cifra (unità, decimi, …)
la loro media può essere approssimata alla cifra successiva (decimi, centesimi, …) se i dati sono almeno una decina, alla seconda cifra successiva (centesimi, millesimi, …) se sono almeno un migliaio, alla terza cifra successiva (millesimi, decimillesimi, …) se sono almeno un centinaio di migliaia, … [aggiungendo 1/2 unità corrispondente alle
cifre finali dei dati originali se questi erano troncati].
Infatti i dati approssimati x1,...,xn differiscono dal
dato esatto per errori ei che cadono in un intervallo ampio u
(u=1 se le approssimazioni sono agli interi, u=0.1 se sono ai decimi, ...).
Nel fare la media, Σxi/n, l'errore complessivo è
Σei/n; è una variabile gaussiana con s.q.m. σ = s/√n essendo s lo s.q.m. degli ei.
Man mano che il numero n dei dati cresce la dispersione dell'errore sul valor medio
(valutata prendendo come "unità di misura" lo s.q.m.) tende a 0, e quindi
il valor medio è man mano più preciso dei dati originali.
Tale errore
tende a 0 come 1/√n; quindi man mano che n viene moltiplicato per 100 esso si divide per 10, ossia si ottiene una precisione relativa
10 volte migliore.
Quindi, quando vogliamo trovare il valor medio relativo ad un certo aspetto di una data popolazione di soggetti attraverso una
indagine statistica, la numerosità del campione, all'aumentare della numerosità della popolazione dei soggetti indagati,
deve crescere meno velocemente di questa: se per una certa indagine su una popolazione di 1000 soggetti usiamo un campione di 50 soggetti e se
vogliamo svolgere un'indagine analoga con esiti confrontabili su una popolazione di 9000 soggetti, dato che √9 = 3, dobbiamo utilizzare
un campione di 50·3 soggetti.
L'ultima cifra della media così approssimata può
differire di una o due unità dalla corrispondente cifra del valore che si sarebbe ottenuto approssimando i dati originali. Per avanzare di un posto
nella approssimazione "avendo tutte le cifre buone" avremmo dovuto prendere non 10 ma 100 dati, e quindi una decina di migliaia, un milione, ... di dati per prendere due, tre, ... cifre in più rispetto ai dati originali.
Infatti se i dati sono approssimati alla cifra di unità u, la
media può essere arrotondata a una cifra in più se l'errore è
al massimo mezza dell'unità 10 volte più piccola, ossia 0.05u.
Gli ei si disperdono uniformemente su un intervallo ampio u; il loro s.q.m. è s = u/√12 e lo s.q.m. dell'errore medio se n=100 è σ = u/√12/√n = u/√1200 = 0.029u:
al 68% l'errore è al più 0.029u, al 95% è al più
2σ* = 0.058u; quindi è molto alta (91%, come si può verificare)
la probabilità che la cifra in più
sia buona. Con probabilità 99.7% è al
più 3σ = 0.087u < u/10, quindi è
praticamente certo che l'errore non superi un'unità sull'ultima cifra.
 Approfondimenti: misurazioni ad alta sensibilità
Approfondimenti: misurazioni ad alta sensibilità
Un cronometro (o un comune orologio al quarzo di tipo digitale) che visualizza i centesimi di secondo è uno strumento a bassa sensibilità
( calcolo approssimato):
se venisse avviato e arrestato il cronometro più volte, facendo trascorrere sempre lo stesso tempo T tra l'avvio e l'arresto, sul visore si leggerebbe sempre lo stesso tempo. Se ad esempio si leggesse 3.27 vorrebbe dire che T è compreso tra 3.27 sec e 3.28 sec, cioè che [3.27,3.28] è un intervallo di indeterminazione "certo" per la misura di T in secondi.
calcolo approssimato):
se venisse avviato e arrestato il cronometro più volte, facendo trascorrere sempre lo stesso tempo T tra l'avvio e l'arresto, sul visore si leggerebbe sempre lo stesso tempo. Se ad esempio si leggesse 3.27 vorrebbe dire che T è compreso tra 3.27 sec e 3.28 sec, cioè che [3.27,3.28] è un intervallo di indeterminazione "certo" per la misura di T in secondi.
Analogamente, se si usa un doppio decimetro per misurare la lunghezza L di un oggetto, si individua la tacca più vicina alla estremità dell'oggetto e, se ad es. questa rappresenta 13.4 cm, si prende 13.4 cm±1/2 mm come approssimazione certa di L, cioè [13.35,13.45] come intervallo di indeterminazione per il valore (in cm) di L.
Per fare un esempio semplice ma reale di misurazione ad
alta sensibilità consideriamo un reflettometro per la determinazione del tasso glicemico del sangue
(viene depositata una goccia di sangue su una striscetta, che viene inserita nello strumento; questo, mediante un opportuno dispositivo ottico, effettua il rilevamento ed esprime il valore in mg/dl). In dotazione è presente (per verificare il corretto funzionamento dell'apparecchio) una striscia di controllo trattata in modo da avere caratteristiche corrispondenti
a quelle di una goccia di sangue con un certo tasso glicemico.
|
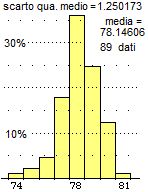
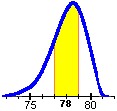
Se ripeto più volte la misurazione del "tasso glicemico" della striscia di controllo non ottengo sempre lo stesso valore. A destra è riprodotto l'istogramma relativo a 89 rilevamenti.
|
|
 |
 |
Le variazioni tra un rilevamento e l'altro sono dovute a una serie di fattori casuali (in cui intervengono aspetti ottici, elettronici, …) che non è possibile né eliminare né conoscere esattamente, per cui il valore letto è da interpretare come una variabile casuale. Aumentando le prove l'istogramma
si stabilizza sulla rappresentazione della legge di distribuzione;
i centri delle sue basi superiori potrebbero collocarsi su una curva simile a quella a sinistra.
Come faccio a decidere in che modo approssimare la misura ottenta? |
Nel caso della striscia di controllo, sottoposta a quasi un centinaio di rilevamenti, posso dire che il valore medio (o valore "atteso")
è 78.1. Con più precisione che è 78.146...±3·1.25.../√88 (con probabilità del 99.7%), cioè 78.15±0.40 (mg/dl)
(vedi qui per l'elaborazione dei dati).
Ma non è detto che questo sia il valore vero del tasso glicemico della striscia di controllo,
è solo il valore atteso della variabile casuale
"esito di un rilevamento per la striscia di controllo". |
Posso comunque osservare che l'istogramma, pur avendo una "coda" a sinistra, ha forma quasi simmetrica, e ipotizzare quindi che gli errori casuali siano sia positivi che negativi e che le misure rilevate tendano a cadere attorno alla
misura "vera", e posso supporre che questa sia "circa" (a meno di 1 unità) 78 (vedi parte colorata sul grafico sopra a sinistra).
Se faccio un rilevamento per una certa persona non ha senso
effettuare molte prove e calcolare il valor medio: in brevi intervalli di tempo il tasso può cambiare (per cui ripetendo la prova non è detto che si effettui sempre la misurazione della stessa grandezza) e, poi,
non interessano valutazioni molto precise. Tenendo conto dello studio effettuato
sulla striscia di controllo possiamo stimare in circa 5 unità lo scarto
che il valore letto può avere dal valore vero e associare alla misura letta tale precisione: se leggo 93, assumo che il tasso glicemico sia 93±5 mg/dl.
 Consideriamo una misurazione ad alta sensibilità per cui abbia
invece senso effettuare più rilevamenti.
Consideriamo una misurazione ad alta sensibilità per cui abbia
invece senso effettuare più rilevamenti.
Un cronometro (o un comune orologio di tipo digitale) che visualizza i centesimi di secondo è uno strumento a bassa sensibilità:
se venisse avviato e arrestato il cronometro più volte, facendo trascorrere sempre lo stesso tempo T tra l'avvio e l'arresto, sul visore si leggerebbe sempre lo stesso tempo.
Se ad esempio si leggesse 3.27 vorrebbe dire che T è compreso tra 3.27 sec e 3.28 sec, cioè che [3.27,3.28] è un intervallo di indeterminazione "certo" per la misura di T in secondi.
Ma se il cronometro è azionato manualmente, misurando sempre lo stesso intervallo di tempo si possono ottenere valori diversi. Ad esempio se avvio e arresto la misurazione man mano che un altro orologio scatta di 1 sec, non troverò, in genere, esattamente 1 sec, ma potrò trovare, via via che ripeto la misurazione, 1.06, 59.93, 59.99, 1.04, 59.95, ...
L'apparato uomo+cronometro è più "sensibile" in quanto ogni volta interviene un errore casuale pari alla differenza tra il temp. o (casuale) con cui l'uomo ritarda l'avvio del cronometro e il tempo (casuale) con cui l'uomo ritarda l'arresto di esso. Se ci si limitasse a leggere i secondi, l'apparato sarebbe invece a bassa sensibilità: gli errori casuali sono dell'ordine dei centesimi di secondo, per cui sarebbe trascurabile la loro influenza.
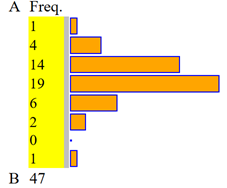
Nel file
t_sec sono registrati i 47 valori in centesimi
di secondo ottenuti da una persona misurando manualmente con un orologio il tempo che impiega un altro orologio a scattare in avanti
di 1 s. La misura vera è quindi 1 sec.
Facciamo finta di non conoscerla e vediamo come potremmo cercare di determinarla.
Ma, prima di fare i conti, riflettiamo: con il cronometro leggo i valori troncati ai centesimi di secondo, quindi per avere una valutazione corretta devo aggiungere 1/2 centesimo di secondo. Lo faccio direttamente sui dati, altrimenti dovrei aggiungerlo al valore ottenuto. I dati corretti sono nel file t_sec_2. Analizziamoli con "calcolatrice2" (vedi). Ottengo:
mean = 99.86170212765957
3*sigma = 4.7494904334723
Rappresentiamo i dati anche con "istogramma".
Otteniamo l'istogramma a destra, abbastanza simmetrico rispetto alla media.
E, in effetti, ha senso ritenere che il rilevamento manuale dia luogo a scostamenti positivi e negativi dal valore "vero" che si compensano.
Aumentando il numero dei rilevamenti vedremmo più chiaramente questa simmetria.
| | 
A = 65, B = 135, 7 intervalli di ampiezza 10 |
Nell'ipotesi che le misure si distribuiscano in modo tendenzialmente simmetrico intorno alla misura vera, possiamo assumere la media come stima della misura vera (infatti se la funzione densità ha grafico simmetrico, l'asse di simmetria deve intersecare l'asse orizzontale in corrispondenza della media).
Come valutare la precisione con cui la media approssima la misura vera?
Supposto – come è ragionevole fare in questo
frangente – che l'apparato non sia affetto da errori sistematici (cioè che l'orologio non
vada avanti o indietro in modo significativo e che l'uomo non ritardi sistematicamente una della
due pressioni – quella di avvio o quella di arresto – maggiormente dell'altra), possiamo dire,
ad esempio, che la misura vera è 99.86 ± 4.75 al 99.7%. Possiamo dire che (con pratica "certezza") è 100±5 (cs).
 Tutto questo
(assumere la media come stima della misura vera) vale nell'ipotesi di simmetria attorno
alla misura vera fatta inizialmente, che (come visto per il
Tutto questo
(assumere la media come stima della misura vera) vale nell'ipotesi di simmetria attorno
alla misura vera fatta inizialmente, che (come visto per il  reflettometro)
non vale in generale.
Supponiamo, ad es., di avere un dispositivo che misuri le velocità di oggetti indirettamente,
rilevando il tempo che ogni oggetto impiega per percorrere 1 m. Supponiamo che l'oggetto viaggi esattamente
alla velocità di 1 m/s, che essa sia misurabile più volte e che i tempi rilevati siano quelli
contenuti in t_sec_2. Il dispositivo ogni volta divide 100 per il tempo rilevato, in modo da ottenere velocità in m/s.
I calcoli sono fattibili facilmente con "calcolatrice2"; QUI gli esiti.
reflettometro)
non vale in generale.
Supponiamo, ad es., di avere un dispositivo che misuri le velocità di oggetti indirettamente,
rilevando il tempo che ogni oggetto impiega per percorrere 1 m. Supponiamo che l'oggetto viaggi esattamente
alla velocità di 1 m/s, che essa sia misurabile più volte e che i tempi rilevati siano quelli
contenuti in t_sec_2. Il dispositivo ogni volta divide 100 per il tempo rilevato, in modo da ottenere velocità in m/s.
I calcoli sono fattibili facilmente con "calcolatrice2"; QUI gli esiti.
 | |
A sinistra il grafico ottenibile con "istogramma"
e, sotto, i valori ottenibili con "calcolatrice2":
mean = 1.0137085137582602
3*sigma = 0.05174192155496886
|
Si può osservare che l'istogramma è meno simmetrico e che
la media ha distanza relativa dal valore vero (1.014 differisce da 1 dell'1%) maggiore rispetto a quanto
accadeva per i tempi (99.86 differiva da 100 dello 0.1%). Con più misurazioni avrei l'illusione di ottenere precisioni man mano migliori ma otterrei invece un intervallo di indeterminazione che si stringe attorno a un valore diverso dalla misura vera:
la media delle misure rilevate non converge alla misura vera. In conclusione, di fronte a un apparato come quello in questione, si dovrebbe, combinando studi sperimentali e riflessioni teoriche, individuare una legge di distribuzione delle misure e individuare quale variabile statistica, diversa dalla media sperimentale, assumere come stimatore della misura vera.
Nel caso di pochi dati (10 o 20), comunque, anche se l'andamento non è molto simmetrico (ma neanche troppo "asimmetrico"), poiché σ rimane grande, si può assumere media±3σ come intervallo di indeterminazione "praticamente certo" della misura vera.
Esercizio 2 (soluz.)
Esercizio 3 (soluz.)
Esercizio 4 (soluz.)
Esercizio 5 (soluz.)


 leggi di distribuzione - var. discrete), se passo dall'esito della ripetizione molte volte del lancio di due dadi a quello del lancio di quattro, ho che l'istogramma tende ad avere una forma a "campana".
Vedi i successivi istogrammi (dadi(4)non bilanciati).
leggi di distribuzione - var. discrete), se passo dall'esito della ripetizione molte volte del lancio di due dadi a quello del lancio di quattro, ho che l'istogramma tende ad avere una forma a "campana".
Vedi i successivi istogrammi (dadi(4)non bilanciati).










