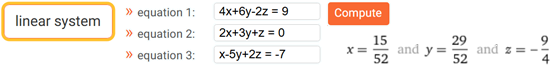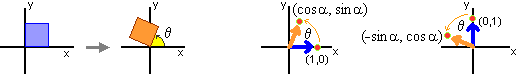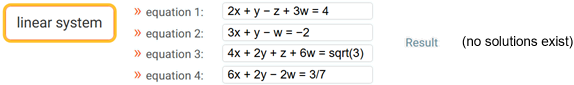Le matrici

A lato sono riprodotte due tabelle (quanto hanno speso tre persone per A e per B in due anni consecutivi) e la tabella somma (quanto hanno speso, per A e per B, nel complesso dei due anni):  tabelle delle stesse dimensioni si possono sommare membro a membro, allo stesso modo di come si fa per i vettori nello spazio bidimensionale o nello spazio tridimensionale.

'07 A B Tom  81 17 91 15 77 13 Dick  Harry

'08 A B Tom  88 19 93 16 76 18 Dick  Harry

tot A B Tom  81+88 17+19 91+93 15+16 77+76 13+18 Dick  Harry

100 ( 81  17 )  =  ( 8100  1700 )  91  15 9100  1500 77  13 7700  1300

Come nel caso dei vettori, possiamo moltiplicare tutti gli elementi di una tabella per un numero che, anche in questo caso, chiamiamo scalare.  Tabelle di dati e operazioni di questi tipi su di esse sono spesso usate anche in statistica. Vediamo, ora, qualche altro uso meno evidente.

    Abbiamo considerato i sistemi lineari a 2 equazioni e 2 incognite, e abbiamo visto che il loro comportamento (in particolare quante soluzioni hanno e che cosa rappresentano graficamente) dipende dalle relazioni che intervengono tra i vari coefficienti.  Ad esempio il sistema  4x+6y = 9 AND 2x+3y = 0  nelle incognite x ed y non ha soluzioni, mentre  x+y = 0 AND 2x−y = 5  ha le soluzioni x = 5/3, y = −5/3.

I due sistemi possono essere riassunti con delle tabelle e delle operazioni tra esse come quelle a fianco, che li fanno diventare simili a delle equazioni di primo grado. Chiariamo il significato della operazione "×" (prodotto) tra tabelle che compare.

( 4  6 ) × ( x )  =  ( 9 )       ( 1   1 ) × ( x )  =  ( 0 ) 2  3 y 0 2  −1 y 5

    Affinché vi sia una equivalenza con i sistemi di partenza occorre che le espressioni precedenti siano uguali a quelle sottostanti.

Quindi il "×" tra una tabella 2×2 e una tabella 2×1 deve dar luogo a una tabella 2×1 la cui prima riga − 4x+6y, riferendoci al primo esempio − sia il frutto di una "moltiplicazione" della riga "4 6" per la colonna "x y", e la cui seconda riga − 2x+3y − sia il frutto di una "moltiplicazione" della riga "2 3" per la colonna "x y".

( 4x + 6y )  =  ( 9 )       (  x + y )  =  ( 0 ) 2x + 3y 0 2x − y 5

    Nel secondo esempio il prodotto della riga "1 1" per la colonna "x y" diventa x+y, quello della riga "2 −1" per la colonna "x y" diventa 2x−y.  In entrambi i casi abbiamo inteso il prodotto  "riga × colonna"  come il prodotto scalare "·" ( vettori) tra la riga e la colonna in questione.

In modo analogo, il sistema a 3 equazioni e 3 incognite  4x+6y−2z = 9 AND 2x+3y+z = 0 AND x−5y+2z = −7  può essere rappresentato nel modo a destra. Il termine a sinistra della seconda equazione del sistema, ad esempio, può essere ottenuto moltiplicando la riga (2 3 1) per la colonna (x y z).

( 4   6  −2 ) × ( x )  =  (  9 ) 2   3    1 y  0 1  −5   2 z −7

    Ricordiamo che i sistemi lineari (come già ricordato) possono essere risolti facilmente con lo script "sistemi di equazioni" (vedi qui):

    Se volessi i risultati sotto forma di frazione potrei usare lo script "frazioni":
      28/100 + 846153/99999900 → 15/52     55/100 + 76923/9999990 → 29/52     225/100 → 9/4

    Ovvero posso usare WolframAlpha:

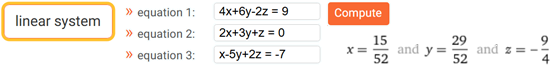
    Le tabelle, dotate di queste operazioni di addizione, di prodotto per una scalare e di moltiplicazione, vengono chiamate matrici. Ovviamente occorre tener conto che due matrici per essere sommate devono avere la stessa dimensione (nel primo esempio erano entrambe 3×1), in modo da poter sommare gli elementi che, nelle due matrici, stanno nello stesso posto.  E che per essere moltiplicate devono avere la prima tante colonne quante righe ha la seconda (nell'ultimo esempio una era 3×3, l'altra 3×1, e ho moltiplicato, ad esempio, la riga  2 3 1, costituita da 3 colonne, per la colonna  x y z, costituita da 3 righe).

    Tutti i calcoli che coinvolgono le matrici possono essere svolti facilmente con WolframAlpha.  Qui una banca di esempi.  Se (aperto WolframAlpha) digiti "matrices sum" e "matrices product" puoi eseguire facilmente somme e prodotti di matrici.

Facciamo, ancora, due esempi. Il valore calorico di proteine, grassi e glucidi è, rispettivamente, 4.1, 9.3 e 4.1 kcal/g (valori arrotondati). La tabella A indica, approssimativamente, la percentuale (ovvero il numero di grammi per 100 grammi di sostanza) di proteine, grassi e glucidi (1ª, 2ª, 3ª colonna) dei gamberetti e della maionese che una azienda impiega per produrre un particolare tipo di alimento. Che cosa rappresenta il prodotto A×B?

A =    8    1    55   14 1 3

B =    4.1   9.3 4.1

A×B =    8·4.1+1·9.3+55·4.1   14·4.1+1·9.3+3·4.1

=    267.6   79.0

Le righe della tabella prodotto (che è una tabella 2×1, essendo ottenuta moltiplicando una tabella 2×3 con una 3×1), che posso approssimare a 270 e 80, rappresentano, in questo caso, il totale delle chilocalorie fornite da 1 hg di ciascuna sostanza.

Come altro esempio pensiamo alle rotazioni attorno all'origine, limitandoci, per semplicità al caso piano. Le rotazioni di multipli di 90° ( numeri complessi) è facile descriverle usando le matrici: a destra è descritta la rotazione di −90°.  Più in generale è facile descrivere mediante matrici una qualunque rotazione ampia α attorno all'origine:

( 0  −1 ) × ( x )  =  (  y )  1   0 y −x

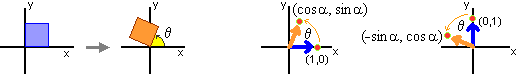(clicca l'immagine per ingrandirla)

Infatti (come permette di dedurre la figura precedente, e come si può vedere alla voce numeri complessi) il punto (1,0) viene trasformato nel punto (cos(α), sin(α)), il punto (0,1) viene trasformato nel punto (−sin(α), cos(α)) e, in generale, il punto (x,y) viene trasformato nel punto rappresentato vettorialmente a destra.

cos(α)   −sin(α)    ×    x    =    x·cos(α) − y·sin(α)    sin(α)    cos(α) y x·sin(α) + y·cos(α)

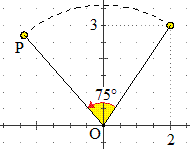
Sotto, a sinistra è illustrato come viene trasformato il punto (2,3) da una rotazione di 75° attorno all'origine e, a destra, come si possono individuare le sue coordinate moltiplicando il vettore che lo rappresenta per la matrice che rappresenta la rotazione di 75°.
	cos(75°)   −sin(75°)    ×    2    =    2·cos(75°) − 3·sin(75°)    =    2.380…    sin(75°)    cos(75°) 3 2·sin(75°) + 3·cos(75°) 2.708…

    Sottoporre un punto a due rotazioni, α e β, attorno all'origine equivale a ruotarlo una sola volta di una quantità pari alla somma, α+β, delle due rotazioni. Formalizzando queste considerazioni si arriva a dimostrare che  A×(B×C) = (A×B)×C, ossia che per il prodotto tra matrici vale la proprietà associativa ( strutture numeriche e non).  Non vale, invece la proprietà commutativa, anzi, non è detto che se si può fare A×B si possa fare anche B×A: basta, ad esempio, che A sia 2×3 e B sia 3×1.

  Per completare, almeno ad un primo livello, le considerazioni sulle matrici occorre mettere a punto i concetti di matrice identità e di matrice inversa. Ciò ci permetterà, ad esempio, di trovare un modo di risolvere in forma compatta sistemi come quelli considerati sopra ().  Per mettere a punto questi concetti ci soffermiamo sulle matrici quadrate, ossia sulle matrici che hanno tante colonne quante le righe.
    Una matrice identità è una matrice quadrata che ha 1 come elementi che stanno sulla diagonale che parte dal primo posto della prima riga e ha 0 come altri elementi.  Data una matrice M, viene chiamata sua matrice inversa, e indicata M⁻¹, una matrice che moltiplicata a destra o a sinistra per M dà la matrice identità. Ad esempio abbiamo:

I =    1    0   0 1

A =    1    2   −1 0

B =    0    −1   1/2 1/2

A×B = I

B×A = I

B = A−1

A = B−1

Infatti, se data una matrice M indichiamo con m _{i, j} il suo elemento che sta nella riga i-esima e nella colonna j-esima, abbiamo che l'elemento di posto 1,1 di A×B è  a _1,1 b _1,1 + a _1,2 b _2,1 = 1·0+2·1/2 = 1 (riga e colonna evidenziate in giallo), quello di posto 1,2 è  a _1,1 b _1,2 + a _1,2 b _2,2 = 1·(−1)+2·1/2 = 0, quello di posto 2,1 è  a _2,1 b _1,1 + a _2,2 b _2,1 = −1·0+0·1/2 = 0, quello di posto 2,2 è  a _2,1 b _1,2 + a _2,2 b _2,2 = −1·(−1)+0·1/2 = 1.

    La matrice nulla (tutti gli elementi uguali a 0) ovviamente non ha l'inversa, ma non ce l'ha, ad esempio, anche la seguente matrice A:

A =    4    6   2 3

B =    x    y   u v

A×B =    2h    2k    ≠  h k

1    0   0 1

h = 2x+3u k = 2y+3v

Infatti, qualunque sia B, A×B ha la prima riga pari al doppio della seconda, e quindi non può essere uguale ad I.

    È facile verificare (facendo il prodotto) che, se A è una matrice quadrata 2×2, la sua matrice inversa è data dalla seguente formula:

A =    a    b   c d

A−1 =  1 ———— a·d − b·c

d    −b   −c  a

    Nel primo caso considerato in questo paragrafo ritroviamo facilmente che A⁻¹ = B. Nel secondo caso troveremmo a·d − b·c = 12−12 = 0, a conferma che questa A⁻¹ non può essere individuata, ossia che A non ha inversa.
    Se proviamo con WolframAlpha per la seconda matrice A otteniamo il messaggio che non ha inversa nella forma "matrix is singular". Per calcolare a·d − b·c utilizziamo il secondo comando sotto riportato:

  È un po' noioso, ma non difficile, generalizzare questi concetti e queste proprietà a matrici quadrate di qualsiasi ordine. Vediamo come definire il determinante delle matrici 3×3, che abbiamo già introdotto in un caso particolare considerando le proprietà dei vettori nello spazio tridimensionale:

si calcola il prodotto del primo elemento della prima riga per il determinante della matrice 2×2 che si ottiene eleminando la prima riga e la prima colonna;  a questo si aggiunge, cambiato di segno, il prodotto del secondo elemento della prima riga per il determinante della matrice che si ottiene eleminando la prima riga e la seconda colonna;  a questo si aggiunge, non cambiato di segno, il prodotto del terzo elemento della prima riga per il determinante della matrice che si ottiene eleminando la prima riga e la terza colonna.  In breve, nel caso della matrice A a lato:

A =    1   −1    3   1     0   −1 2     1     6

det(A) = 1·det(0,−1; 1,6) − (−1)·det(1,−1; 2,6) + 3·det(1,0; 2,1) =
1·(0−(−1)) − (−1)·(6−(−2)) + 3·(1−0) = 1+8+3 = 12

Volendo, potevo scambiare la prima e la seconda riga, ossia studiare la matrice a fianco. Il suo determinante è: det(B) = 1·det(−1,3; 1,6) + (−1)·det(1,−1; 2,1) = −9 − 3 = −12.  A causa dello scambio, come nel caso 2×2, si ha un cambio segno:  det(A) = −det(B) = 12.

B =    1     0   −1   1   −1    3 2     1     6

Nel caso di una matrice 4×4, come quella a lato, si procede in modo simile: det(A) = 2·det(1,0,−1; 2,1,6; 2,0,−2) − 1·det(3,0,−1; 4,1,6; 6,0,−2) + (−1)·det(3,1,−1; 4,2,6; 6,2,−2) − 3·det(3,1,0; 4,2,1; 6,2,0) det(1,0,−1; 2,1,6; 2,0,−2) = 1·det(1,6; 0,−2) − 0·det(…) + (−1)·det(2,1; 2,0) = −2 + 0 + 2 = 0 ecc.

A =    2   1   −1    3   3   1     0   −1 4   2     1     6 6   2     0   −2

Ma si può scambiare posto alla 2ª e alla 4ª in modo da ricondursi alla matrice B a fianco, le cui ultime due righe sono proporzionali. Si può concludere che il determinante è nullo. Infatti i determinanti delle matrici 2×2 delle ultime due righe sono nulli e da questo si ricava che sono nulli anche quelli delle matrici 3×3 delle ultime tre righe e, quindi, anche quello della matrice 4×4.  Anche se avessi trovato due colonne proporzionali avrei potuto concludere che il determinante è nullo: scambiando righe e colonne, infatti, il determinante non cambia.  Per inciso osserviamo che quando due righe o due colonne U e V di una matrice, o due vettori U e V, sono proporzionali, ossia quando esiste un numero reale h tale che U = h V, si dice che U e V sono linearmente dipendenti. La cosa può essere generalizzata a tre o più vettori: U, V e W sono linearmente dipendenti quando uno di essi, ad esempio U, può essere espresso come h V +k  W.

B =    2   1   −1    3   4   2     1     6 3   1     0   −1 6   2     0   −2

    Con WolframAlpha, battendo  det{{2,1,-1,3},{3,1,0,-1},{4,2,1,6},{6,2,0,-2}}  otterremmo 0.

Esercizio  e  soluzione

Vediamo, infine, come applicare questi concetti alla soluzione dei sistemi lineari.     I sistemi lineari a 2 equazioni e due incognite considerati sopra possono essere riscritti nella forma  A×X = B, dove con A abbiamo indicato la matrice 2×2 dei coefficienti di grado 1 e con B la marice 2×1 dei termini noti, mentre con X abbiamo indicato la matrice 2×1 delle incognite.

X =  ( x ) y

Se moltiplichiamo a sinistra entrambi i membri (che sono equivalenti a matrici 2×1) per A−1 abbiamo l'esito a fianco. Ma nel primo caso A ha determinante 0 in quanto la prima riga, (4 6), è proporzionale alla seconda, (2 3), per cui l'operazione non si può fare, e il sistema non ha soluzioni.  Nel secondo caso, invece, ritroviamo:

X = A−1×B

det(A) = −1−2 = −3

A−1 =  1 — −3

2    −1   1  1

X =

1 — −3

2    −1   1  1

×

0   5

=

5/3   −5/3

Nel caso del sistema a lato, possiamo metterlo in forma matriciale A×X = B dove A è la matrice 4×4 considerata nel paragrafo precedente.  La matrice A ha, come abbiamo visto alla fine del paragrafo precedente, determinante nullo, quindi non riesco a trasformare il sistema esplicitando un'unica quaterna (x, y, z, w) di soluzioni.     Siamo come nel caso  a x = b  con a = 0:  le soluzioni possono essere infinite (0·x = 0), o nessuna (0·x = 3).

{ 2x + y − z + 3w = 4 3x + y − w = −2 4x + 2y + z + 6w = √3 6x + 2y − 2w = 3/7

x    = ? y z w

    Nel nostro caso abbiamo una situazione analoga:  A×X = B con det(A) = 0. In questo caso stabilire se le soluzioni sono infinite o nessuna è un po' meno "automatico". Qui ci fermiamo senza sviluppare l'argomento, che potrà affrontare chi proseguirà in studi di tipo scientifico. Vediamo solo come affrontare tali questioni con WolframAlpha e con lo script "sistemi equazioni".

    WolframAlpha ci informa se non esistono soluzioni o ci fornisce sottoforma di equazione le infinite soluzioni:

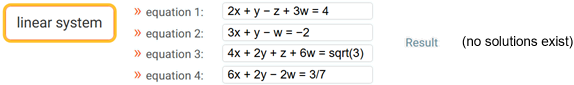
    Lo script indica con "SING" (sistema "singolare") tutti i casi in cui non c'è una sola soluzione:

Esercizio  e  soluzione

  Notiamo che la parte della matematica che si occupa di sistemi lineari, vettori e matrici viene chiamata algebra lineare.  Il nome deriva dal termine inglese line che significa "retta" (mentre il termine italiano "linea" comprende anche le curve).  Le equazioni lineari  a x + b y + c = 0  in due variabili rappresentano rette; con i sistemi di due equazioni lineari di due variabili si possono rappresentare le intersezioni di coppie di rette, e quindi i punti.  Le equazioni lineari in tre variabili, a x + b y + c z + d = 0, rappresentano piani (vedi); con i sistemi di due equazioni lineari di tre variabili si possono rappresentare le intersezioni di coppie di piani, e quindi le rette.