Potenze (1)

#1  Per esprimere numeri molto grandi o molto piccoli è comodo ricorrere alle potenze. Se a è un numero qualunque, positivo o negativo, e n è un numero intero non negativo, si pone:

anè  1 moltiplicato ripetutamente n volte per a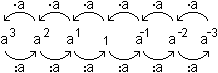 
a0è  1
a–n è  1 diviso ripetutamente n volte per a

Ad esempio:

• 1000000, cioè 1 con l'aggiunta di 6 zero, cioè 1 spostato 6 posti a sinistra, cioè 1 moltiplicato 6 volte per 10, può essere scritto 10 6;

• 1, cioè il numero 1 senza spostamenti, può essere scritto 10 0;

• 0.00001, cioè 1 spostato 5 posti a destra, cioè 1 diviso 5 volte per 10, può essere scritto 10-5.

 
    Ricordiamo che  a²  e  a³  sono letti, oltre che come  "a alla 2" o "a alla seconda"  e  "a alla 3" o "a alla terza",  anche come "a al quadrato" e "a al cubo" in quanto corrispondono all'area e al volume di un quadrato e di un cubo di lato a.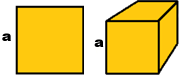    

#2   Valgono le formule seguenti [dove n, m sono numeri interi], che sono facili da (ricavare e) ricordare pensando alla figura iniziale (moltiplicare/dividere per a vuol dire aumentare/diminuire l'esponente di 1): 

                                   m
  -n    1       m  n    m+n       a     m-n
 a   = ———     a ·a  = a         ——— = a
         n                         n
        a                         a

Ad esempio per calcolare 107/10-5 posso fare: 107/10 –5 = 107 – (– 5) = 107+5 = 1012.

#3  Dati due numeri x e y (con y intero), la funzione che ad essi associa il numero x y viene chiamata operazione di elevamento a potenza. Il risultato xy si legge «x alla y» o «potenza y-esima di x».

#4  Nota1. x y è definito anche per x = 0 e y > 0: 0 y = (1 moltiplicato y volte per 0) = 0. Invece per x = 0 e y ≤ 0 x y è indefinito: infatti, se volessi usare le formule sopra riportate, dovrei avere, ad es. 0-2 = 1/02 = 1/0. Del resto di fronte a  0 [xy] 2 [+/-] [=] una calcolatrice visualizza un messaggio d'errore, come farebbe nel caso di  1 [ : ] 0 [=].

#5  Nota2. L'operazione di elevamento a potenza è definita anche per esponenti non interi. Infatti una calcolatrice di fronte a  4 [xy] 7.5 [=]  non segnala errori. Vedremo in seguito [  Potenze (2),  Strutture numeriche] il significato di xy per y non intero.

#6  Nota3. Si può rappresentare l'elevamento a potenza anche senza ricorrere a una scrittura "a due piani" (uno per la base e uno per l'esponente): si può infatti usare il simbolo di operazione "^". Ad esempio 27 verrebbe scritto come 2^7 ("^" rappresenta una "freccia in su"). Questa è la scrittura impiegata in molte applicazioni per il calcolatore (linguaggi di programmazione, fogli di calcolo, …).

Esercizi:   testo1  e  soluz.,   testo2  e  soluz.,   testo3  e  soluz.,   testo4  e  soluz.,   testo5  e  soluz.
 

Altri esercizi per la scuola di base