Il piano cartesiano
Come modello matematico per caratterizzare posizioni "esatte" su una superficie piatta (di cui abbiamo come prototipi la parte superiore di un tavolo, una piazza senza rilievi o affossamenti e con il fondo liscio, la parete di un muro, la superficie di uno stagno, …), generalizzando l'uso delle coordinate nelle carte geografiche, posso considerare le coppie (x,y) di numeri reali.
L'insieme di queste coppie viene chiamato piano numerico o piano cartesiano o, più semplicemente piano.
L'aggettivo "cartesiano" deriva da Descartes, latinizzato in Cartesius, nome di un grande studioso francese - che si occupava di filosofia, scienze, matematica - vissuto nel 17° secolo che è tra coloro che hanno introdotto e sviluppato l'uso di numeri ed equazioni numeriche per descrivere le figure geometriche.
L'idea
è quella di pensare il piano come un reticolato costituito
dall'intersecarsi perpendicolarmente di due schiere di rette
numeriche parallele dette, rispettivamente, assi orizzontali e assi
verticali.
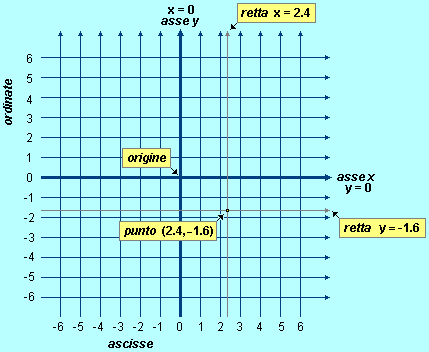
Gli
assi che si incontrano nei rispettivi punti 0 vengono detti asse
x e asse y.

Le
posizioni che sugli assi orizzontali corrispondono a 1 sono
attraversate da una stessa retta verticale; anche le posizioni
corrispondenti a 2 sono attraversate da una stessa retta verticale;
più in generale, le posizioni k, qualunque sia il
numero k, sono attraversate dalla stessa retta verticale, che
viene indicata con x=k.
Analogamente,
qualunque sia il numero k, le posizioni che sugli assi
verticali corrispondono a k sono attraversate dalla stessa
retta orizzontale, che viene indicata con y=k.
Il
punto (2.4, –1.6) è rappresentato
dall'intersezione delle rette x=2.4 e y=–1.6; 2.4 viene
detto prima coordinata o ascissa, –1.6 viene
detto seconda coordinata o ordinata.
Il
punto (0,0) viene chiamato origine (degli assi).
Il piano cartesiano può essere dotato di diverse distanze. Le più usate sono le seguenti:
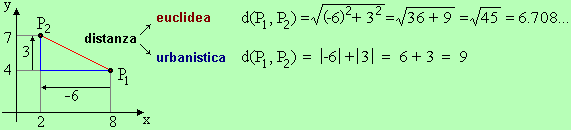
Dati due punti P1 = (x1, y1) e P2 = (x2, y2), se indichiamo con Δx la variazione orizzontale da P1 a P2 e con Δy quella verticale, la distanza euclidea è così definita:
d(P1, P2) = √( (Δx)2 + (Δy)2 ) = √( (x2 – x1)2 + (y2 – y1)2 )
Questo concetto di distanza (quello in genere impiegato per il piano cartesiano) è un modello matematico della distanza in linea d'aria. Si basa, evidentemente, sul teorema di Pitagora.