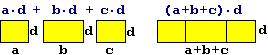Termini equivalenti

  Due termini vengono detti algebricamente equivalenti quando assumono gli stessi valori, cioè: comunque sostituisco valori alle eventuali variabili che compaiono in essi, ottengo due termini che sono entrambi definiti o entrambi indefiniti e, nel primo caso, hanno lo stesso valore.

  Ad esempio a+b+c può essere riscritto nella forma: c+a+b o nella forma: b+(c+a). Con qualche calcolo a mano su alcuni esempi numerici è facile convincersi che i nuovi termini sono algebricamente equivalenti al termine originale:

2+3+9 = 5+9 = 14		9+2+3 = 11+3 = 14		3+(9+2) = 3+11 = 14
8+7+2 = 15+2 = 17		2+8+7 = 10+7 = 17		7+(2+8) = 7+10 = 17

    La dimostrazione che ciò valga in generale è molto complicata.
    Possiamo convincerci di questa equivalenza interpretando "fisicamente" la addizione:
se cambio l'ordine con cui congiungo tre aste non cambia la lunghezza dell'oggetto che ottengo.

    Con un analogo ragionamento "fisico" posso convincermi che equivalenze simili valgono anche nel caso di una quantità diversa di addizioni, cioè che in generale vale la cosiddetta proprietà del riordino della somma:
due termini ottenuti entrambi applicando ripetutamente l'addizione a partire dagli stessi sottotermini t₁, t₂, …, t_n sono termini equivalenti.

Analogamente, interpretando la moltiplicazione come modello matematico per il calcolo dell'estensione di una superficie rettangolare, posso convincermi del fatto che:     a·d+b·d+c·d equivale a (a+b+c)·d
e più in generale del fatto che:     a(b + c + …) = ab + ac + …  e  (b + c + …)a = ba + ca + … cioè che vale la cosiddetta proprietà distributiva della moltiplicazione rispetto alla addizione.

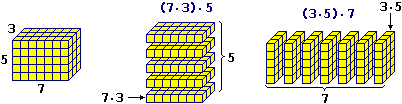
  Con ragionamenti fisici ed esperimenti numerici (ad es. osservando che per contare i cubetti della figura seguente posso sia sommare 5 strati di 7·3 cubetti, cioè fare 7·3·5, che sommare 7 strati di 3·5 cubetti, cioè fare 3·5·7) possiamo convincerci che vale anche la proprietà del riordino del prodotto:
due termini ottenuti entrambi applicando ripetutamente la moltiplicazione a partire dagli stessi sottotermini t₁, t₂, …, t_n sono termini equivalenti.

  Per calcolare 17+29+13·118 con una CT senza priorità conviene considerare 13·118+17+29. Il nuovo termine è equivalente al termine iniziale in base alla proprietà del riordino della somma.
    Per precisare in che modo è stato riordinato il termine possiamo dire che abbiamo applicato la regola di riscrittura  a+b+c → c+a+b  (a è 17, b è 29, c è 13·118). Si è già usata questa notazione alla voce  formule.
   La direzione della freccia indica il verso in cui viene effettuata la sostituzione.
   A volte la stessa riscrittura viene indicata con a+b+c ← c+a+b (qui la freccia è alla rovescia: indica che l'espressione a destra "subentra" al posto di quella a sinistra) o con a+b+c = c+a+b o con a+b+c := c+a+b.
Nota 1.  Parlando di "applicare regole" non si vuol dire che, nel calcolo algebrico, ci sono procedimenti standard per i diversi tipi di problemi a cui occorre attenersi. Stiamo usando la parola "regola" per indicare uno schema, una descrizione sintetica di una particolare trasformazione, fra le varie che possono essere scelte e combinate per risolvere un certo problema.

  È utile, soprattutto finché si è dei "principianti", svolgere i calcoli di tipo algebrico provando a esplicitare (a parole o con una regola di riscrittura), ogni volta che si fa un passo durante la trasformazione di un termine, il procedimento che si è impiegato. Questo aiuta a controllare se sono presenti errori. Si rallenta un po' la velocità di calcolo, ma questa non è la cosa più importante: l'importante è non commettere errori.
    In caso di incertezza (nel trovare il procedimento da usare o nel controllo della regola scelta o della sua applicazione) può essere utile fare qualche esempio numerico o pensare a qualche situazione d'uso, di tipo geometrico-fisico (come visto sopra) o di altro genere: ad es. il ricordo che premendo 2 volte [1/x] sul visore ricompare il numero di partenza può suggerire la regola 1/(1/a) → a.
    Del resto, ai nostri giorni, anche i calcoli simbolici vengono svolti utilizzando opportuni programmi al calcolatore. Ciò che occorre è scrivere i termini correttamente (cioè seguendo il linguaggio - convenzioni, simboli, … - utilizzato dal programma che si impiega) e dare man mano i comandi giusti per effettuare le trasformazioni che ci interessano. E per entrambe queste cose occorre avere chiara la  struttura del termine su cui si opera e saper individuare le  regole di riscrittura che si vogliono applicare.

  Riepiloghiamo le più comuni "regole di riscrittura" che si possono applicare per trasformare termini in termini ad essi algebricamente equivalenti, indicando anche il modo in cui vengono in genere descritte verbalmente, dai matematici e nelle applicazioni di calcolo simbolico. Su altri aspetti del calcolo algebrico si torna in altre voci [risoluzione di equazioni, di sistemi, …]. Tieni conto che:
•  nelle regole riportate nei riquadri le lettere rappresentano generici sottotermini;
•  dopo ai riquadri è un link ad alcune avvertenze per l'uso, con l'indicazione di alcuni errori che spesso vengono compiuti applicando malamente queste regole;

rimpiazzamento (o sostituzione) di un sottotermine t1 con un sottotermine t2 equivalente ...t ... 2 ... t ... ———> 1 ...(t )... 2

Es.:  2xy + yx  →  2xy + xy  (t₁ è yx, t₂ è xy), e poi  →  3xy:  usando il fatto che yx è equivalente a xy posso sostituire yx con xy ottenendo un termine equivalente a quello di partenza.

Es.:  se so che Spese = Spesa1+Spesa2, da Guadagno = Incasso - Spese ottengo Guadagno = Incasso - (Spesa1+Spesa2), non Guadagno = Incasso - Spesa1+Spesa2.

riordino di addizioni e moltiplicazioni casi particolari: a+b+c ———> c+a+b o b+a+c o … abc ———> cab o bac o …

eliminazione delle negazioni --a o -(-a) ———> a

Es.:  7 [+/−] [+/−]  →  7

eliminazione dei reciproci -1 1 -1 —— o (a ) o … ———> a 1 — a -1 a b (——) ———> —— b a

Es.:  0.2 [1/x] [1/x]  →  0.2

• portar fuori la negazione da un prodotto • eliminazione (2 a 2) delle negazioni in un prodotto a(-b) o (-a)b ———> -ab (-a)(-b) ———> ab

Es.:   −(−3 · −2 · −1) = −(3 · 2 · −1) = − −(3 · 2 · 1) = 3 · 2 · 1 = 6

distribuzione (→) e raccoglimento (←) della negazione rispetto all'addizione ———> -(a+b+…) -a - b - … <———

distribuzione (→) e raccoglimento (←) del reciproco rispetto alla moltiplicazione 1 ———> 1 1 ——— — — ab <——— a b

Es.:     x·1/(3xy)·y  =  x·1/3·1/x·1/y·y  =  x·1/x·y·1/y·1/3  =  1·1·1/3  = 1/3

trasformazioni di divisioni ab ba a/b ———> a —— o —— o ——— —— cd bc c/b <——— c a — b ———> a —— o a/b/c ——— c <——— bc a ac a c —— o a/(b/c) ———> —— o — c o a — b b b b — c

moltiplicazione per zero ———> a·0 o 0·a o 0/a 0 <———

distribuzione (→) della moltiplicazione rispetto all'addizione e raccoglimenti (←) ———> a(b+c+ …) ab + ac + … <———

Es.:   3/7 + 5/7 = 1/7·(3+5) = (3+5)/7
          98·7 = (100-2)·7 = 100·7-2·7 = 700-14 = 686
          (a+b)·(c+d) = a·(c+d) + b·(c+d) = ac+ad + bc+bd

distribuzione (→) della potenza e della radice rispetto alla moltiplicazione e raccoglimenti (←) c ———> c c (ab) a b <——— √(ab) ———> √a √b <———

Es.:   (30)² = (3·10)² = 3²·10² = 9·100 = 900
          √8·√2 = √(8·2) = √16 = 4
          √0.04 = √(4/100) = √4/√100 = 2/10 = 0.2

raggruppare i termini di  una somma  un prodotto 3 3 es.: 3+6a-5-b +a ———> -b +7a-2 o 3 7a-b -2 o … -2 5 4 2 2 4 es.: a ba ba ———> a b o b a

particolari "semplificazioni" a - a ———> 0 a - ———> 1 a

    Spesso, applicando queste "regole di riscrittura", e impiegando i modi di dire discussi nel prossimo paragrafo, si commettono vari tipi di errori:   esempi di errori.

fattorizzare	In questo modo vengono spesso chiamati i raccoglimenti a fattor comune e le distribuzioni di potenze e radici rispetto alla moltiplicazione  [con fattore si intende un termine di una moltiplicazione]
portar dentro portar fuori	Con "portar fuori" (da una potenza, da una radice, da una somma,…) in genere si indicano delle fattorizzazioni. Ad es. portar fuori z da √(xyz) dà luogo a √z·√(xy), portar fuori z da 2kz+kxz dà luogo a (2k+kx)z. Con "portar dentro" si intendono le trasformazioni opposte: portar z dentro alla somma trasforma (2k+kx)z in 2kz+kxz, portar z dentro alla potenza trasforma z4(xy)2 in (z²xy)2.
semplificare	In questo modo vengono spesso chiamate le trasformazioni che si ottengono applicando raggruppamenti di somme e di prodotti, il primo esempio di trasformazioni di divisioni, oltre all'effettuazione di eventuali calcoli numerici (2+3 = 5, …) o basati sulle proprietà di 0 e di 1 o delle potenze.
sviluppare o espandere	In questo modo vengono spesso chiamate le trasformazioni che si ottengono applicando distribuzioni della moltiplicazione rispetto alla addizione (con cui si passa da un termine con parentesi a un termine senza parentesi), e trasformazioni di divisioni (con cui si passa da termini a più "piani" a termini a soli due "piani"), oltre all'effettuazione di eventuali calcoli numerici o basati sulle proprietà di 0 e di 1 o delle potenze.
Un aggettivo spesso usato è irriducibile, sia per indicare una frazione non ulteriormente semplificabile, sia per indicare un termine che, in un particolare ambito (da precisare caso per caso), non è ulteriormente fattorizzabile.

    Ricordiamo alcune trasformazioni di  formule che, spesso, vengono utilizzate per effettuare delle manipolazioni assieme a quelle per trasformare termini:

 Nota 2. Spesso invece di termini algebricamente equivalenti si parla più semplicemente di termini equivalenti. Occorre però aggiungere la specificazione "algebricamente" quando si vuole fare una distinzione da altri tipi di equivalenza:
due termini possono essere algebricamente equivalenti ma non essere equivalenti dal punto di vista della precisione del calcolo (se i calcoli vengono eseguiti con un mezzo di calcolo che opera con una quantità fissata di cifre i due termini possono dar luogo a due risultati differenti) o dal punto di vista del tempo di calcolo.

    Consideriamo ad esempio  123456789012 - 123456789012 + 1/80  e  123456789012 + 1/80 - 123456789012,  che sono algebricamente equivalenti, calcolati con un linguaggio di programmazione standard (JavaScript):
    document.writeln(1/80)
    document.writeln(123456789012 + 1/80 - 123456789012)
    document.writeln(123456789012 - 123456789012 + 1/80)
valgono   0.0125   0.0124969482421875   0.0125.
    Con questa piccola calcolatrice online ottengo:
123456789012 + 1/80 - 123456789012  →  0.012496948242
123456789012 - 123456789012 + 1/80  →  0.0125

    Dopo questo esempio di non equivalenza dal punto di vista della precisione, facciamo un esempio relativo al tempo di calcolo.  Eseguendo "mano", con l'usuale algortimo per la moltiplicazione, il calcolo di  7×254  è molto più dispendioso di quello di  254×7.