Intuitivamente, due figure piane sono uguali se, ricalcata una figura su un vetro (o su un altro materiale trasparente che, appoggiato sul piano, si mantenga rigido), posso far scorrere il vetro fino a che la copia che ho fatto si sovrappone esattamente all'altra figura.  In altre parole se esiste un movimento piano che trasforma una nell'altra.  La figura F e la figura A della illustrazione 1 sono dunque uguali rispetto a questa accezione, così come lo sono il pesce in basso a destra e il pesce in alto a sinistra della illustrazione 2 (uno è ottenibile dall'altro con una rotazione di 180° attorno all'origine); esse non sono invece uguali al terzo pesce della stessa illustrazione:  non sono sovrapponibili ad esso con un movimento piano (occorre un ribaltamento).  In genere è questo il modo in cui è usato l'aggettivo "uguale" quando si confrontano figure del piano.

    Però potremmo convenire di chiamare uguali anche le figure tra loro simmetriche, ossia tutte le figure tra loro isometriche.  In tal caso diremmo che tutti e tre i pesci sono uguali.  Questa scelta corrisponde alla situazione in cui si dice che  «Luisa ha le mani uguali, mentre Maria ha la mano destra più grande della sinistra»:  le mani di Luisa sono uguali nella seconda accezione  (sono simmetriche: una è uguale alla immagine allo specchio dell'altra), non nella prima.  Nella seconda accezione due triangoli con i lati uguali sono uguali, mentre nella prima potrebbero non esserlo: 

    Nel linguaggio comune spesso vengono considerate uguali due figure della stessa forma anche se di dimensioni diverse, come le figure F e B della illustrazione 1 o i pesci U e V della illustrazione 3:  si pensi a due tessuti ricamati o stampati che presentano lo stesso tipo di figure.  In matematica ciò consisterebbe nel chiamare uguali due figure trasformabili una nell'altra mediante una similitudine.

    Se invece dicessimo che due figure sono uguali quando sono uguali gli insiemi di punti che le costituiscono, avremmo che una figura è uguale solo a sé stessa.  Implicitamente usiamo questo concetto di uguaglianza nella frase «r e s sono rette diverse e parallele» per escludere che r e s siano coincidenti.  Infatti se usassimo una delle precedenti accezioni di uguaglianza, non ci sarebbero rette tra loro diverse, ossia non uguali:  ogni retta è trasformabile in una qualunque altra retta mediante una rotazione e una traslazione.

    L'uso di "uguale" in matematica ha significati diversi a seconda dei contesti e delle convenzioni man mano adottate.  Per un altro esempio si pensi a 12/4 e 3:  hanno struttura diversa (uno contiene due costanti, l'altro è costituito da una sola costante) ma a volte si dice che sono uguali, nel senso che hanno lo stesso valore.

    Si possono fare considerazioni analoghe per il simbolo "="  (20/3 = 6.67 in un contesto in cui si considerano approssimazioni ai centesimi, x = 3.2 ± 0.1 sta per 3.2-0.1≤x≤3.2+0.1)  e per la parola "equivalente"  (due termini possono essere algebricamente equivalenti ma non essere equivalenti dal punto di vista della precisione del calcolo o dal punto di vista del tempo di calcolo).

1  -  Alcune diverse trasformazioni della figura F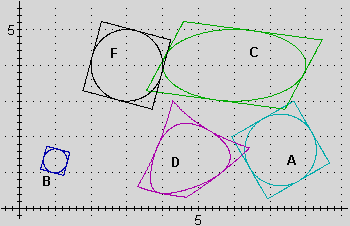

2  -  Due diverse trasformazioni del pesce in alto a destra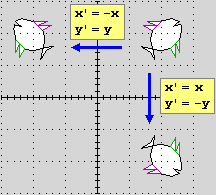

3  -  Due successive trasfornazioni del pesce U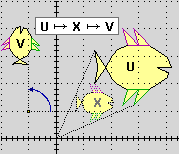