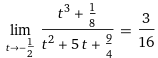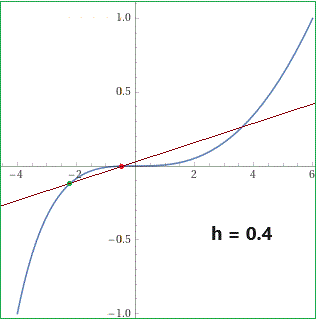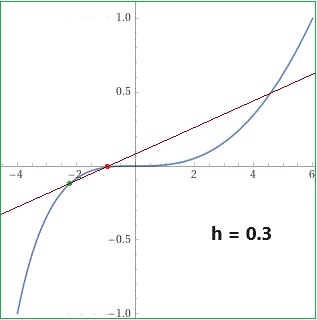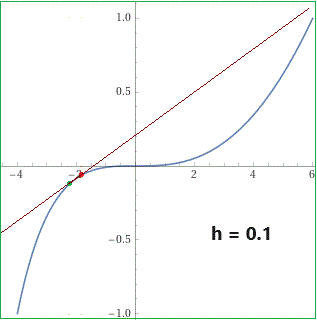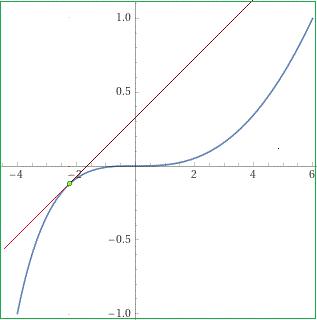
Il grafico della curva costituita dai punti: x = t*(t+5), y = t^3  per t che varia da -1 ad 1 Qual è la tangente alla curva nel punto P = (-9/4,-1/8), colorato a fianco in verde, che corrisponde a t = -1/2? A fianco la retta che passa per P e per un punto Q sulla curva (colorato in rosso) che man mano si avvicina e tende a coincidere con P. Più precisamente Q è il punto che corrisponde a t = -1/2+h  per h che vale  0.4, 0.3, 0.2, 0.1.

La tangente alla curva nel punto (-9/4,-1/8) colorato in verde, che corrisponde a t = -1/2, ha pendenza 3/16. Perché?

Calcolo la variazione di y e di x tra tale punto e quello corrispondente a t
Δy = t^3 -(-1/8)       Δx = t*(t+5)-(-9/4)       Δy/Δx = (t^3+1/8)/(t^2+5*t+9/4)
Devo calcolare il limite di Δy/Δx al tendere di t a -1/2.   Uso WolframAlpha:
Introduco     (t^3+1/8)/(t^2+5*t+9/4), t -> -1/2     e ottengo: