Osservazioni fatte prima delle correzioni e degli annullamenti di vari
quesiti operati dal ministero.
[vari testi sono formulati in modo sbagliato o sottointendendo convenzioni ed
altri aspetti non specificati; varie risposte sono formulate in modo errato;
eccetera, ... (valgono considerazioni simili per i quesiti di scienze e di fisica)]
Come verificare (e correggere ...) con WolframAlpha alcune soluzioni: esempi per la 49.
limit 2/(3+4*log(x)) as x -> 0+
# la risposta indicata dal Ministero è sbagliata
sum (-1)^(n-1)*pi^(2*n-2)/factorial(2*n-2), n=1 to oo
# il testo nel quiz è errato: il primo termine è 1 non π
trapezoidal rule
3/4/2*(exp(0)+2*exp(3/4)+2*exp(3/2)+2*exp(3*3/4)+exp(3))
# 19.97189503867732431162154436... -> 19.972
# nel testo la risposta è giusta, ma è la domanda che è sbagliata: l'integranda
# è x -> exp(x), non x -> x*exp(x)
# (ovviamente è da intendere l'approssimazione alla 3^a cifra decimale frazionaria)
...
Come verificare con WolframAlpha alcune soluzioni: esempi per la 47.
integrate sin(2*x)^5*cos(2*x) dx
# sin(2x) = t, dt/dx = 2*cos(2x), cos(2x)*dx = 1/2*dt, integrate t^5/2 dt
integrate sin(2*x)*exp(sin(x)^2) dx from x=0 to pi/2
# e^(sin^2(x)) tra 0 e pi/2
lim exp(-x)*sin(x) as x->oo
(integrate x*log(x) dx from 1 to e)/(e-1)
integrate sin(x)^2 dx from 0 to 1
# plot sin(x)^2 from x=0 to 1
# 0+2*(sin(1/4)^2+sin(1/2)^2+sin(3/4)^2)+sin(1)^2)/8
d/dx (integrate exp(-t^2) from t=2*x to 3*x)
sum k^2, k=1 to n
sum (2/3)^n, n=1 to oo
2*sin(2pi/20)
x^4-2*x^3-3*x^2-2*x+6
3*(5/(1+2^2))
d^2/dx^2((1+x/20)^5)
(20+40)^3/160000
exp(-i*pi/2)
fields medal
year 1687
euclid's elements
# clicca "more details" (vedi anche: http://mathworld.wolfram.com/EuclidsTheorems.html)
# Volendo, potrebbe essere utile sapere che e' tra il 7^ e il 10^, non so quale
# forma di 'cultura' dimostri che distinge l'8^ dal 9^ ...
parametric plot (3*sin(t), 2*cos(t))
det ({{1,2,3},{4,-2,3},{0,5,-1}})
inv({{2,5},{1,3}})
100!+1
2^sqrt(2)
(1/(1+10)+1/(2+10)+...+1/(10+10)
(1/(1+100)+1/(2+100)+...+1/(100+100)
(1/(1+1000)+1/(2+1000)+...+1/(1000+1000)
sum 1/(k+10000000) k=1..10000000
sum 1/(k+n) k=1..n
arc length of y=2*(x/3)^2 from x=0 to x=27
integrate(sqrt(9+16*x^2)) from 0 to 9
triangle area
abs(z1*z2)
base
# selezionare "a computation" e poi "base to convert from"
binomial[n,n-k]-binomial[n,k]
binomial[n,k-1]+binomial[n,k]-binomial[n+1,k]
binomial[n-1,k-1]-binomial[n+1,n-k]
# molti quesiti erano affrontabili pensando a casi particolari
#- ad es. "Due sfere di raggi R e r sono tangenti tra loro e a uno
# stesso piano in A e B. AB vale ..." Basta pensare al caso R=r
# e si ha subito che l'unica risposta accettabile e' 2√(Rr)
#- A0x^n+...An con Ai interi e p/q radice: basta pensare a 2x+3=0
# (A0=2, An=3, p=3, q=-2) per accettare solo "p divide An e q A0"
...
# Nota 1: ∞ equivale a quello che (in "alcuni" settori avanzati della matematica
# - geometria proiettiva, ... - non affrontabili nella scuola secondaria superiore)
# viene indicato con +∞ (cerca infinity in WolframAlpha)
# (va però osservato che in alcuni manuali universitari di analisi matematica di autore
# italiano si considera anche il limite all'infinito senza segno: forse era meglio
# non prevedere fra le risposte possibili "non esiste", che, secondo questa
# interpretazione, sarebbe stata la risposta corretta)
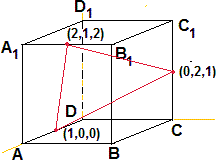
# Nota 2: nel quesito "siano K, L e M i punti medi degli spigoli AD, A1B1 e CC1 del cubo
# A B C D A1 B1 C1 D1 . Il triangolo KLM è:" le risposte "rettangolo" e "isoscele" andavano
# intese con le aggiunte "non isoscele" e "non equilatero", e nel testo occorreva pensare
# ABCD e A1B1C1D1 come facce opposte, AA1 come lato, .... Nel caso sotto raffigurato
# i lati del triangolo sono tutti lunghi quanto le radici di 1^2+1^2+2^2 (il t. è equilatero)
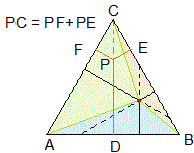
 # "P punto interno a triangolo equilatero. La somma delle distanze di P
# dai lati del triangolo ..." Da uno schizzo come il seguente posso intuire
# che la somma delle distanze è pari all'altezza. Forse la dimostrazione
# più semplice è pensare al fatto che i tre triangoli aventi i lati
# del triangolo originale come lato e P come vertice opposto (nel disegno
# collocato nel pallino rosso) hanno area pari all'intero triangolo: lato*(h1+h2+h3) = lato*h,
# da cui h1+h2+h3=h
# "P punto interno a triangolo equilatero. La somma delle distanze di P
# dai lati del triangolo ..." Da uno schizzo come il seguente posso intuire
# che la somma delle distanze è pari all'altezza. Forse la dimostrazione
# più semplice è pensare al fatto che i tre triangoli aventi i lati
# del triangolo originale come lato e P come vertice opposto (nel disegno
# collocato nel pallino rosso) hanno area pari all'intero triangolo: lato*(h1+h2+h3) = lato*h,
# da cui h1+h2+h3=h
 (quiz presente in molti test, facile ... se uno lo ha già visto)
(quiz presente in molti test, facile ... se uno lo ha già visto)
 # "P punto interno a triangolo equilatero. La somma delle distanze di P
# dai lati del triangolo ..." Da uno schizzo come il seguente posso intuire
# che la somma delle distanze è pari all'altezza. Forse la dimostrazione
# più semplice è pensare al fatto che i tre triangoli aventi i lati
# del triangolo originale come lato e P come vertice opposto (nel disegno
# collocato nel pallino rosso) hanno area pari all'intero triangolo: lato*(h1+h2+h3) = lato*h,
# da cui h1+h2+h3=h
# "P punto interno a triangolo equilatero. La somma delle distanze di P
# dai lati del triangolo ..." Da uno schizzo come il seguente posso intuire
# che la somma delle distanze è pari all'altezza. Forse la dimostrazione
# più semplice è pensare al fatto che i tre triangoli aventi i lati
# del triangolo originale come lato e P come vertice opposto (nel disegno
# collocato nel pallino rosso) hanno area pari all'intero triangolo: lato*(h1+h2+h3) = lato*h,
# da cui h1+h2+h3=h
 (quiz presente in molti test, facile ... se uno lo ha già visto)
(quiz presente in molti test, facile ... se uno lo ha già visto)