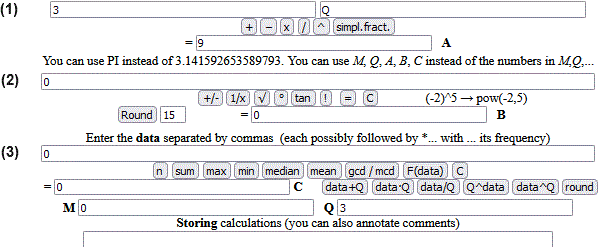
(1)        +      -      x      /      ^      simpl.fract.         A  
(2)    +/-      1/x      √      °      tan      atan      !      =      C       
  functions  
  Round        B  
(3)        n      sum      max      min      median      mean        
  gcd/mcd       F(data)        C  
  data+Q      data·Q      data/Q       Q^data      data^Q      round  
  C      M      Q  

[ 5 ]   [ 4 ]   [+]
  9
[ 5 ]   [ 1/3 ]   [+]
  5.333333333333333
[ 5 ]   [ 1/3 ]   [-]
  4.666666666666667
[ 2 ]   [ 3.5 ]   [x]
  7
[ 100 ]   [ 7 ]   [/]
  14.285714285714286
[ 8 ]   [ 1/3 ]   [^]
  2
[ 48 ]   [ 54 ]   simpl.fract.                     see d —> m/n
  48 / 54 = 8 / 9
[ pow(2,3) ]   [ 5 ]   [x]       pow(2,3) is 2^3 = 2*2*2 = 8
  40
In  A  the result of (1) appears or you can write a number; then you can use A as input in other boxes
Put 1 in A then [ 2 ] [ A ] [x]  [ 2 ] [ A ] [x] ...
I have (in A) 2 4 8 16 32 64 ...

[ 5 ]   [+/-]
  -5
[ 5 ]   [1/x]
  0.2
[ 25 ]   [√]
  5
[ 180 ]   [°]
  3.141592653589793     (angle expressed as length of arc of radius 1 wide 180°)
[ 45 ]  [°]
  0.7853981633974483 (the result is in B); then:
[ B ]   [tan]
  1             tan (tangent) is the slope of the angle
[ 1 ]   [atan]
  0.7853981633974483 = 45 ^ (= 45°)
[ 8/100]  [atan]     0.07982998571223732 = 4.573921259900861^ (≈ 4.6°)
      <- 4.5739…°
[ 9 ]   [!]
  362880     (= 9*8*7*6*5*4*3*2*1)
[ 1+5*6-1/2 ]   [=]
  30.5             (the value of the term)
[C] resets the value in (2)
In (2) I can use other functions:

abs(a) / |a|                     min(a,b)                    max(a,b)
sqrt(a) / square root of a                   cbrt(a) / cube root of a
pow(a,b) / a to the power b                       sign(a) / sign of a
round(a) / integer closest to a       trunc(a) / integer portion of a
tan(a) / tangent of a          atan(a) / the angle whose tangent is a
                  M%%N is the remainder of M/N

Example:
[ cbrt(8)*pow(5,3) ]   [=]
  250       (2*125)
[ 12345.6789 ]     [Round] [ 0 ]    12346    [Round] [ 1 ]   12345.7
                   [Round] [ -3 ]   12000    [Round] [ 3 ]   12345.679  
In  B  a result appears or you can write a number; then you can use B as input in other boxes

Unlike the behavior of pocket calculators, the computer operates with numbers in a somewhat different way, so the results of the operations may differ by a few units on the last digit (see). However, they are more digits than are usually needed. With this calculator we can Round numbers. An example:
[ 11/5 - 2 + 1/4 + 7/20 ] [=]
  0.8000000000000002           [Round] [ 15 ]  —> 0.8

You can also use Round by putting in (2) A, B, C, M or Q.

[ 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6 ]   [n]
  11
[ 1.5*4, 3*6, 4*10 ]   [n]
  20
[ 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6 ]   [sum]
  6
[ 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6 ]   [max]
  6
[ 1.5*4, 3*6, 4*10 ]   [max]
  4
[ 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6 ]   [min]
  -5
[ 7, 8, 1, 9, 5, 3 ]   [median]
  5     median=5 (or 7)
                      Here  ->  to order numbers
[ 7, 8, 1, 9, 5, 3 ]   [mean]
  5.5
[ 12, 28, 44 ]   [ gcd/mcd ]
  gcd = Mcd = 4     lcm = mcm = 924

If I put (for example) in (2) 5+2*Q, in (3) the data 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
and I click [F(data)] I have 5+2*0, 5+2*1,...,5+2*10:
5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25

[ ..., ..., ... ]   [C]
  [ ]   (the data ..., ..., ... is cancelled)

[ 1,-1, 0, 2, 3, 5 ]   [data+Q]   [2] in Q
  [ 3, 1, 2, 4, 5, 7 ]
[ 1,-1, 0, 2, 3, 5 ]   [data·Q]   [2] in Q
  [ 2, -2, 0, 4, 6, 10 ]
[ 1,-1, 0, 2, 3, 5 ]   [data/Q]   [2] in Q
  [ 0.5, -0.5, 0, 1, 1.5, 2.5 ]
[ 1,-1, 0, 2, 3, 5 ]   [Q^data]   [2] in Q
  [ 2, 0.5, 1, 4, 8, 32 ]
[ 1,-1, 0, 2, 3, 5 ]   [data^Q]   [2] in Q
  [ 1, 1, 0, 4, 9, 25 ]
[ 2.374, -321.6666, 56 ]   [round]   [0] near Round
  [ 2, -322, 56 ]
[ 2.374, -321.6666, 56 ]   [round]   [-1] near Round
  [ 0, -320, 60 ]

In  C  a result appears or you can write a number; then you can use C as input in other boxes
In  M  you can write a number; then you can use M as input in other boxes
In  Q  you can write a number; then you can use Q as input in other boxes
Use "C", "M", "Q", not "c", "m", "q".

                          Expressing a Decimal as a Fraction
1.45             ->  145/100   ->  simpl.fract.  (29/20)
0.777...         ->  7/9
0.373737...      ->  37/99
0.070707...      ->  7/99
0.627627627...   ->  627/999   ->  simpl.fract.  (209/333)
0.027027027...   ->  27/999    ->  simpl.fract.  (3/11)
0.00627627627... ->  627/99900 ->  simpl.fract.  (209/33300)
5.3627627627... -> 5.3+0.0627627627... = 53/10+627/9990 = (53*999+627)/9990 -> simpl.fract.
 [ 53*999+627 -> 53574, 53574/9990 -> 8929/1665, check: 8929/1665 -> 5.362762762762763 ]
0.791666... -> (791.666...)/1000 = (791+2/3)/1000 = (791*3+2)/3000 = 2375/3000 -> simpl.fract.
 [ 791*3+2 -> 2375, 2375/3000 -> 19/24, check: 19/24 -> 0.791666666666667 ]

You can use WolframAlpha (altri esempi):  0.791666... -> 19/24  3.1326326... -> 6259/1998
    [the repetend (periodo) must be written at least 2 times followed by ...)

If I compute 1.27-1.23 I have 0.040000000000000036, not 0.04. Why?
In a computer the number are represented with the figures 0 and 1 (not with 0, 1, 2, …, 9). For example the finite decimal number 0.27 (two figures) is represented by
0.01000101000111101011100001010001111010111000010100011110101110...
(i.e.: 0 + 1/2^2 + 1/2^6 + 1/2^8 + 1/2^12 + 1/2^13 + 1/2^14 + 1/2^15 + 1/2^17 + ...)
The figures are now innumerable, but che computer can keep only a finite number of them. So the number is not exactly represented.
0.040000000000000036 is the representation with 0, 1, 2, … and 9 of the final result with 0 and 1.
 

abs(a)     / |a|                            log10(a) / log of a base 10
acos(a)    / arc cosine of a                max(a,b)
asin(a)    / arc sine of a                  min(a,b)
atan(a)    / arc tangent of a               pow(a,b) / a to the power b
atan2(a,b) / arc tangent of a/b             random() / random n. in [0,1)
cbrt(a)    / cube root of a                 round(a) / integer closest to a
ceil(a)    / integer closest to a not < a   sign(a)  / sign of a 
cos(a)     / cosine of a                    sin(a)   / sine of a
exp(a)     / exponential of a               sqrt(a)  / square root of a
floor(a)   / integer closest to a not > a   tan(a)   / tangent of a
log(a)     / log of a base e                trunc(a) / integer portion of a
log2(a)    / log of a base 2                PI       / π

cosh(a),sinh(a),tanh(a), acosh(a),asinh(a),atanh(a)    hyperbolic functions

      Note:   M%N is the remainder of M/N,   != is "not equal"