•  Un'automobile, mentre sta viaggiando a velocità costante, percorre una distanza di  240 ± 2 m  in  12 ± 0.2 s.  Qual è la sua velocità?

20.01 ± 0.50 m/s, o  20 ± 0.5 m/s.

Il calcolo si potrebbe fare anche con WolframAlpha:

o con un semplice programmino in JavaScript, cambiando la prima riga del programma se cambiano funzione e intervalli:

function F(x,y) {return x/y}; x1=238; x2=242; y1=11.8; y2=12.2
min=1e100; max=-1e100; n=1e4; h=(x2-x1)/n; k=(y2-y1)/n
for(i=0; i<=n; i=i+1) {for(j=0; j<=n; j=j+1) {
  x=x1+i*h; y=y1+j*k; U=F(x,y)
  if(U<min) min=U; if(U>max) max=U }}
centro=min+(max-min)/2; raggio=(max-min)/2
document.write("min="+min+"<br>max="+max+"<br>"+centro+" +/- "+raggio)
                       uscite:
min=19.508196721311478
max=20.508474576271187
20.00833564879133 +/- 0.5001389274798544 

•  Altri esempi:  x * y, x ∈ [3.8,3.9], y ∈ [6.4,6.5]

  x1 3.8   x2 3.9     y1 6.4  y2 6.5
                  [/]
  min 24.32   max 25.35   indet 1.03
            24.835 ± 0.515          24.84 ± 0.52  o  24.8 ± 0.5

•   x ^ y, x = 0.9 ± 0.05, y ∈ [1.39,1.40]

  x1 0.85   x2 0.95     y1 1.39  y2 1.40
                   [^]
  min  0.796501...   max 0.931184...   indet 0.134683...
        0.863842... ± 0.067341...          0.864 ± 0.068  o  0.86 ± 0.07

•   x / y, x = 49 ± 0.5, y = 2

  x1 48.5   x2 49.5     y1 2  y2 2
                    [/]
  min  24.75   max 25.25   indet 0.5
                 25 ± 0.25          25.00 ± 0.25

•   x / y, x ∈ [1+6.5/60, 1+7.5/60], y ∈ [62.45,62.55]

Calcolo prima 1+6.5/60 e 1+7.5/60 con la calcolatrice incoporata, poi procedo:

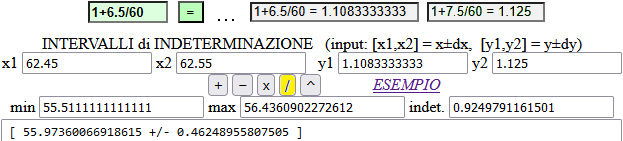
            56.0 ± 0.47  o  56 ± 0.5

Per situazioni più complesse, in cui intervengono altre funzioni, si può facilmente ricorrere ad un programmino in JavaScript, come visto sopra. Un esempio.

So che  A = (u+2^u+v) / v  e che u = 3.2±0.1 e v = 2.5±0.1. Che cosa posso concludere del valore d A?

function F(x,y) {return (x+Math.pow(2,x+y))/y}
x1=3.2-0.1; x2=3.2+0.1; y1=2.5-0.1; y2=2.5+0.1
min=1e100; max=-1e100; n=1e4; h=(x2-x1)/n; k=(y2-y1)/n
for(i=0; i<=n; i=i+1) {for(j=0; j<=n; j=j+1) {
  x=x1+i*h; y=y1+j*k; U=F(x,y)
  if(U<min) min=U; if(U>max) max=U } } 
centro=min+(max-min)/2; raggio=(max-min)/2
document.write("min = "+min+"<br>max = "+max+"<br>"+centro+" +/- "+raggio)
                       uscite:
min = 20.147847498307936
max = 24.236196714752186
22.19202210653006 +/- 2.044174608222125   (22.19±2.05)

Un esempio in cui compaiono 3 variabili.  Con un cartoncino del peso di 300 g al m² (ovvero 0.03 g al cm²) costruisco un triangolo con lati di 10.0, 14.0 e 8.2 cm (quindi con precisione 0.05 = metà del valore 0.1 dell'ultima cifra). Quanto pesa il cartoncino?
L'area del triangolo la ottengo con la formula √( P·(P-2A)·(P-2B)·(P-2C) ) / 4 (se A, B e C sono i lati e P è il perimetro): vedi gli esempi di questo script).

Uso lo script (in cui uso n=1e3 per impiegare meno tempo):

function F(x,y,z) {return Math.sqrt((x+y+z)*(x+y-z)*(x+z-y)*(y+z-x))/4 * 0.03}
x1=10-0.05; x2=10+0.05; y1=14-0.05; y2=14+0.05; z1=8.2-0.05; z2=8.2+0.05
min=1e100; max=-1e100; n=1e3; h=(x2-x1)/n; k=(y2-y1)/n; v=(z2-z1)/n
for(i=0; i<=n; i=i+1) {for(j=0; j<=n; j=j+1) {for(w=0; w<=n; w=w+1) {
  x=x1+i*h; y=y1+j*k; z=z1+w*v; U=F(x,y,z)
  if(U<min) min=U; if(U>max) max=U } } }
centro=min+(max-min)/2; raggio=(max-min)/2
document.write("min = "+min+"<br>max = "+max+"<br>"+centro+" +/- "+raggio)
                       uscite:
min = 1.1925097574777686
max = 1.2288508363221664
1.2106802968999675 +/- 0.018170539422198928

Il cartoncino pesa 1.21±0.02 g