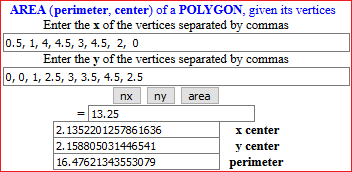
Example:

The graph with WolframAlpha:

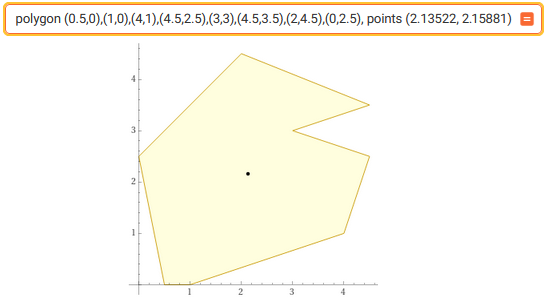
The centroid, also known as geometric center or center of plane figure F, is the center of mass (or barycenter) of a lamina of constant thickness and of a single material having the shape of F. In other words, it is the point at which a cutout of the shape F (with uniformly distributed mass) could be perfectly balanced on the tip of a pin.

Come è calcolata l'area?   vedi
 

Il centroide  (che nel caso di una figura piatta di materiale omogeneo coincide col baricentro)  C  di un poliogno  P1P2…Pn  di area A si può dimostrare  (cerca "polygon centroid Surveyor's Formula" con un motore di ricerca)  che è:

Cx = ( (x1 + x2)·(x1·y2 - x2·y1) + … + (xn + x1)·(xn·y1 - x1·yn) ) / (6A)
Cy = ( (y1 + y2)·(x1·y2 - x2·y1) + … + (yn + y1)·(xn·y1 - x1·yn) ) / (6A)
 

Nota. Non ha alcun senso parlare di angoli esterni di un poligono.  A parte il fatto che non sono angoli del poligono,  nel caso del poligono sopra raffigurato quali sarebbero?  È una delle tante nozioni inutili o errate che vengono spesso fatte studiare a scuola, per buttar via tempo e non affrontare argomenti più importanti.