Le coordinate polari permettono di descrivere facilmente varie curve che non sono descrivibili esprimendo l'ordinata (y) in funzione dell'ascissa (x). Ad es. le seguenti quattro equazioni, che esprimono ρ in funzione di θ espresso in radianti, ρ = 2,  ρ = θ,  ρ = θ2,  ρ = √θ corrispondono ciascuna a una delle quattro curve rappresentate parzialmente a lato, in scale diverse (curve che, come A, C e D, si avvolgono infinite volte attorno ad un punto vengono chiamate spirali).     Per ciascuna equazione trova i valori di ρ corrispondenti a diversi valori di θ (quelli che in gradi valgono 0, 45, 90, 180, 270, 360, 450, 540, …), confronta quanto ottieni con le curve a fianco e associa a ciascuna di queste la relativa equazione.

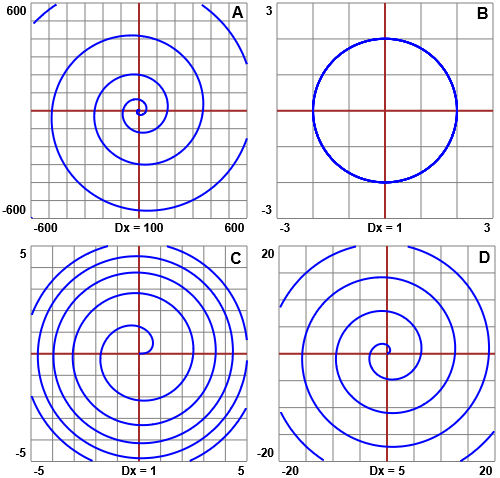ρ = 2 rappresenta un cerchio di raggio 2, quindi ha per grafico B.

ρ = θ è una curva i cui punti hanno distanza dall'origine che aumenta proporzionalmente all'aumento di θ; questo mi fa capire che si tratta di D.

ρ = θ² è una curva i cui punti hanno distanza dall'origine che aumenta più velocemente di quanto aumenti θ: si tratta di A.

ρ = √θ è una curva i cui punti hanno distanza dall'origine che aumenta più lentamente di quanto aumenti θ: si tratta di C.

Un po' di nomi:  ρ = θ, e in generale ρ = k·θ con k > 0 (figura D), viene chiamata spirale di Archimede.
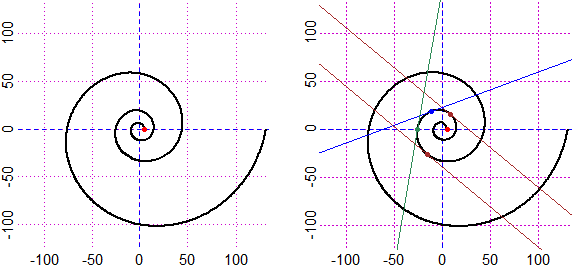
Invece la spirale rappresentata qui sotto, di equazione ρ = 5·2^θ/4, e in generale ρ = k·h^θ·q (k e q positivi), viene chiamata spirale logaritmica.  Come si vede nel grafico a destra, in questa curva, come nel cerchio, man mano che ruoto attorno all'origine degli assi l'inclinazione aumenta proporzionamente (dopo mezzo giro la retta tangente torna ad avere la stessa inclinazione).  Inoltre la velocità con cui ci si allontana dall'origine cresce al crescere della rotazione compiuta (avendo studiato la derivazione, si può concludere ciò osservando che la derivata di una funzione esponenziale è proporzionale alla funzione stessa).  Per approfondimenti vedi Mathworld Wolfram. 

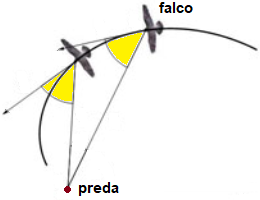
Hanno questa forma, ad esempio, la conchiglia del nautilo e il volo del falco pellegrino quando si avventa su una preda.

Per altre spirali digita "spiral plane curves" in WolframAlpha.

Per le coordinate polari: Lo spazio, Rette tangenti e curve (e I numeri complessi) neGli Oggetti Matematici.