Leggi di distribuzione (variabili discrete)

  Il calcolo delle probabilità studia situazioni in cui, accanto a condizioni che si riescono a valutare, intervengono fattori difficili da determinare che, per semplificare, si dicono essere dovuti al caso.
    Ad esempio ipotizziamo che la compagnia telefonica che utilizzo preveda un costo fisso di CF cent. per chiamata e un costo di CS cent. per ogni secondo di conversazione. Devo chiedere un'informazione per telefono e voglio valutare quanto mi costerà la telefonata;  i valori di CF e CS li posso conoscere a priori (mi basta consultare le condizioni del contratto con la compagnia telefonica) mentre la durata della telefonata dipende da molti fattori (la persona che ha l'informazione risponde direttamente lei alla chiamata? quanto impiega a reperire l'informazione? con che velocità parla? …).
    Se T è il tempo in secondi per cui durerà la telefonata posso esprime il costo in centesimi col termine  CF + CS · T  (CostoFisso + CostoPerSecondo · TempoInSecondi) e, per esempio, l'evento che il costo superi 1 € posso esprimerlo con la formula  CF + CS · T > 100.
    In questa formula CF e CS sono variabili deterministiche, ossia variabili usuali, di cui (note le condizioni del contratto) si può determinare il valore;  invece T è una variabile casuale : il suo valore può variare in relazione a come, il "caso", fa evolvere l'evento.

    T rappresenta una durata temporale, può assumere valori reali positivi qualunque. Nel caso del lancio di un dado la variabile U che esprime il numero uscito può assumere invece solo i valori 1, 2, 3, …, 6.  Variabili casuali che, come T, possono variare, con continuità, su tutto un intervallo di numeri reali vengono dette variabili casuali continue, mentre quelle che, come U, possono assumere solo valori "separati" l'uno dall'altro, elencabili in una successione, vengono dette variabili casuali discrete ("discretus", in latino, è il participio passato di "discernere", che significa "distinguere, separare").
    In questa voce approfondiremo lo studio di queste ultime (clicca le immagini per ingrandirle).

Esercizio (e soluzione)

  Istogrammi di distribuzione di variabili casuali discrete

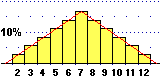A sinistra sono riprodotti gli istogrammi che rappresentano le leggi di distribuzione dell'uscita U del lancio di un dado equo e di quella del lancio di due dadi equi. Come abbiamo visto, questi sono gli istogrammi "limite" degli istogrammi sperimentali: le altezze delle colonne non rappresentano più le frequenze sperimentali, ma (vedi figura a destra, riferita al lancio di un dado) i valori su cui queste tendono a stabilizzarsi, ossia le probabilità.     Nei casi, come questi, di una variabile discreta U che assume valori numerici interi, posso prendere come basi dei rettangolini che formano l'istogramma gli intervallini centrati sui numeri interi; in questo modo la probabilità che U sia n è rappresentata sia dall'altezza del rettangolino con base centrata in n, sia dalla sua area, e l'area dell'intero istogramma vale 100%, ossia 1. Nel primo caso ogni rettangolino è alto 1/6, nel secondo il rettangolino che ha la base centrata nell'ascissa n ha altezza pari a Pr(U=n), ossia a (n-1)/36 se 2≤n≤7, a (12-(n-1))/36 se 7<n≤12.

    Rivedi gli istogrammi generati dai file "dado bilanciato", "dado non bilanciato", "dadi(2)bilanciati", "dadi(2)non bilanciati", "dadi(4)bilanciati" presenti QUI.

    Nello stesso sito, sotto la voce "numeri casuali", accedi agli script "numeri casuali" e "numeri casuali reali", con cui generi dei file di dati che puoi esaminare con lo script "istogramma":

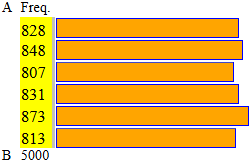		A = 0.5   B = 6.5 6 intervalli di ampiezza 1 n = 5000   min = 1   max = 6 media = 3.5024 Con 100 prove le colonne sarebbero molto diverse,  al loro aumentare tendono ad avere la stessa lunghezza.

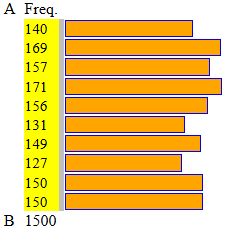		A = 0   B = 1 10 intervalli di ampiezza 0.1 n = 1500 min = 0.0021983563208802 max = 0.9976128764578782 media = 0.489953283095 Anche in questo caso le colonne tendono ad avere la stessa lunghezza. [vedi qui per più dati con meno cifre]

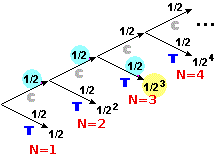
    Osserviamo che una variabile casuale discreta può essere non finita.  Pensiamo al numero N dei lanci di una moneta equa da effettuare fino ad ottenere l'uscita di "testa" (T).
• Al 50% N=1, ossia viene T al primo lancio: Pr(N=1) = 1/2.
• Al secondo lancio ho metà della rimanente probabilità che venga T: Pr(N=2) = (1/2)/2 = 1/4 = 25%.
• La probabilità Pr(N=3) che T venga al terzo lancio è (vedi grafo a destra) (1/2)(1/2)(1/2) = 1/2³ = 1/8 = 12.5%.
• In generale:  Pr(N = h) = 1/2^h
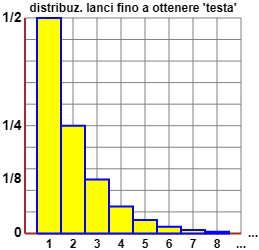
    A sinistra è tracciata (con questo script) parte dell'istogramma di distribuzione di N:  è un esempio di figura illimitata (la base dell'istogramma prosegue senza fine a destra) con area finita (uguale a 1).

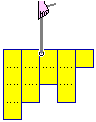
Media teorica     Nel caso di una distribuzione statistica di una variabile numerica, la media corrisponde, sull'istogramma, alla ascissa del centroide (o baricentro) di esso, cioè all'ascissa del punto per cui sospendere la base dell'istogramma in modo che essa resti orizzontale. Anche nel caso dell'istogramma di una legge di distribuzione teorica prendiamo questa ascissa come media teorica della legge di distribuzione.     Ad esempio per l'uscita U del lancio di un dado equo la media teorica è 3.5: infatti, trattandosi di un rettangolo, l'ascissa del baricentro deve stare a metà della base (vedi figura sotto a sinistra). In analogia a quanto fatto per la media di una distribuzione statistica, scriveremo M(U) = 3.5. Esercizio (e soluzione)

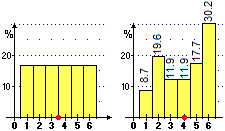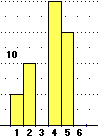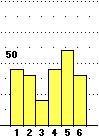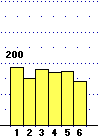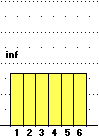
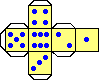
Nel caso di un dado non equo, come quello costruito nel modo illustrato a destra, la media sarà più vicina a 6 (la faccia più leggera, senza linguette incollate) che ad 1 (la faccia più pesante, che difficilmente "esce").     Come possiamo calcolarla usando la sua legge di distribuzione, rappresentata qui a sinistra dal suo istogramma?

    Nel caso statistico la media di una distribuzione X la possiamo ottenere ( Indici di posizione) sommando i prodotti dei valori x_k per le loro frequenze relative fr_k (corrispondenti alle aree delle colonne dell'istogramma sperimentale), nel caso di una variabile casuale X che possa assumere N valori x₁, …,x_N faremo analogamente la somma dei prodotti dei valori x_k per le loro probabilità Pr(X = x_k) (corrispondenti alle aree delle colonne dell'istogramma teorico):

M(X)  =  N (xk· frk) Σ k = 1

diventa:

M(X)  =  N (xk· Pr(X = xk)) Σ k = 1

    Dunque, per il dado non equo ho:

M(U) = (8.7%·1+19.6%·2+11.9%·3+11.9%·4+17.7%·5+30.2%·6) =
(8.7·1+19.6·2+11.9·3+11.9·4+17.7·5+30.2·6)/100 = 4.009 = 4.01 [arrotondando a 3 cifre]

    La media di una variabile casuale X a volte viene chiamata anche speranza matematica o valore atteso ("expected value" in inglese) di X, e indicata E(X).  Nonostante l'aggettivo "atteso" non è detto che si tratti di un valore che la variabile casuale può assumere: nei due casi appena considerati abbiamo ottenuto come medie delle uscite di un dado in un caso 3.5 e nell'altro 4.01, valori che, ovviamente, non possono uscire.  E, come si vede dal secondo esempio, non è detto neanche che sia vicino al valore più probabile (ossia alla moda).

    Qual è la media nel caso del numero N dei lanci da effettuare per ottenere testa considerato sopra?

1/2	+2·1/(22)	+3·1/(23)	+4·1/(24)	+5·1/(25)	...	+10·1/(210)	+... = 2
1/2	1	1.375	1.625	1.78125	...	1.98828125

M(N) = 2.   Se appendessimo un "ipotetico" istogramma di cartoncino di dimensioni infinite come quello di N per un forellino praticato in corrispondenza dell'ascissa 2, esso starebbe in equilibrio.

Nota. In questo esempio l'ultimo "..." sta ad indicare che la somma può proseguire all'infinito. È un'estensione del concetto di somma che, anche se implicitamente, abbiamo già incontrato più volte. Ad esempio la scrittura 1.111…, ad intendere che il numero prosegue con una successione infinita di "1", potrebbe essere sostituita da 1+1/10+1/100+1/1000+…. In questo caso si tratta di una somma che, calcolandola per un numero di addendi via via crescente, si avvicina sempre più ad un numero, appunto a 1+1/10+1/100+1/1000+…, che in questo caso potremmo scrivere anche in forma finita: 1+1/9; infatti 1/9 = 0.111….  Per un esempio analogo ( i numeri), 1.999… = 1+9/10+9/100+9/1000+… = 2.  Ovviamente, non in tutti i casi una "somma infinita" è uguale ad un numero. Ad esempio 1+2+3+4+…, all'aumentare del numero di interi che aggiungo, cresce oltre ogni limite.  È chiaro come, in casi simili a quelli richiamati negli esempi iniziali, si possono usare scritture come ∑ _{k = 0 … ∞} 1/10^k, 1 + ∑ _{k = 1 … ∞} 9/10^k, …, in cui l'uso di ∑ ( indici di posiz. e dispers.) viene esteso al caso di una somma di infiniti addendi.  Nel caso di tutte le leggi di distribuzione ad uscite in un insieme infinito a₁, a₂, a₃, … abbiamo a che fare con una somma infinita di probabilità che vale 1; ad es. nel caso del lancio della moneta abbiamo che ∑ _{k = 1 … ∞} 1/2^k = 1/2+1/4+1/8+1/16+… = 1.

  Nel caso dell'uscita U del lancio di due dadi equi l'istogramma di distribuzione di U ha forma simmetrica rispetto alla retta di ascissa 7: quindi la media è M(U) = 7.
Osserviamo che le distribuzioni U1 e U2 delle uscite dei due singoli dadi hanno media M(U1) = M(U2) = 3.5, e 7 = 3.5+3.5.
In effetti potevamo dedurre che M(U) = 7 da una proprietà più generale:

se X e Y sono due variabili casuali numeriche aventi medie M(X) e M(Y), la variabile casuale X+Y ha media  M(X+Y) = M(X)+M(Y).

Questa proprietà vale sia nel caso sperimentale che in quello teorico, ed è abbastanza evidente; si pensi ad un esperimento con n prove:

M(X+Y) = ((x₁+y₁)+...+(x_n+y_n)) / n = (x₁+...+x_n)/n + (y₁+...+y_n)/n = M(X) + M(Y)

  Data una variabile casuale numerica X diciamo che la media dei valori assunti da X in un certo numero n di "prove" è una media sperimentale (o media empirica o media statistica) di X.  A volte questo numero viene indicato con M_n(X).
    Ad esempio se U è l'uscita di un dado e faccio 20 lanci, la media dei valori così ottenuti è una media sperimentale di U e posso indicarla con M₂₀(U) (tenendo presente, però, che se ripeto i 20 lanci potrei ottenere una media diversa).
    Se chiamo T la tabellina che associa ad 1, 2, 3, …, 6 le rispettive frequenze ottenute con queste 20 prove, T è una distribuzione statistica (ai valori sono associate le frequenze invece delle probabilità) la cui media non è altro che uno dei possibili valori che (in un esperimento di lancio dei dadi) può assumere la media sperimentale di U considerata sopra:  M₂₀(U) = M(T).
    Osserviamo che il simbolo M(…) viene usato indifferentemente per le medie "teoriche" e per le medie "sperimentali": dal contesto si comprende quale interpretazione darne, ossia quando M(X) è riferito a una variabile casuale X o a una distribuzione statistica X.

  Mediana e varianza teorica

    In modo del tutto analogo avviene il passaggio dalla varianza sperimentale a quella teorica, sostituendo le probabilità alle frequenze relative. Considerazioni analoghe valgono per la mediana.
    Per esemplificare il calcolo esaminiamo la variabile casuale U = "uscita del lancio di un dado equo".

• La mediana è un valore u tale che, nel caso sperimentale, ha al più il 50% di uscite minori di esso e al più il 50% maggiori; nel caso teorico la condizione diventa: Pr(U < u) ≤ 1/2 e Pr(U > u) ≤ 1/2. Di valori di tal genere, nel caso del dado, ne abbiamo due, sia 3 che 4; ciò corrisponde al fatto che (vedi ) la retta verticale che taglia a metà l'area dell'istogramma passa per l'ascissa 3.5. Se assumiamo la convenzione di scegliere il primo valore per cui ciò si verifica, diremo che la mediana è 3.

• Calcoliamo la varianza: V(U) = M( ((U-M(U))² ) = "media dei quadrati degli scarti dalla media":
((1-3.5)²+(2-3.5)²+(3-3.5)²+(4-3.5)²+(5-3.5)²+(6-3.5)²)/6 = (2·2.5²+2·1.5²+2·0.5²)/6 = 35/12.
    Quindi lo scarto quadratico medio è sqm(U) = √(35/12) = 1.7078251.

Nel caso del dado non equo la mediana è 4 in quanto:
            Pr(U < 4) = 8.7%+19.6%+11.9% = 40.2%
            Pr(U > 4) = 30.2%+17.7% = 47.9%

  Nel caso dell'uscita U del lancio di due dadi equi, qual è la varianza?
    Anche per la varianza si ha:  Var(X+Y) = Var(X)+Var(Y).   Nel nostro caso:

Var(U1+U2) = Var(U1)+Var(U2) = 35/12 + 35/12 = 35/6.

    Questa proprietà vale, però, se X e Y sono indipendenti, non in generale.
    Si pensi, come "controesempio", al caso in cui X sia il numero sulla faccia superiore di un dado equo e Y sia quello sulla faccia inferiore. Se lancio il dado sia X che Y di distribuiscono uniformemente, con media 3.5 e varianza 35/12. Le facce opposte di un dado hanno numeri che sommati danno 7, per cui X+Y vale sempre 7. La media è dunque 7, in accordo col fatto che 3.5+3.5=7, ma la varianza è 0 in quanto X+Y ha valore costante.

    Non dimostriamo questa proprietà. Potremmo controllarla sperimentalmente.
    Analogamente si può controllare sperimentalmente che se X e Y sono indipendenti vale anche M(X·Y) = M(X)·M(Y). Se si pensa alla definizione di indipendenza la cosa non sorprende.

  La distribuzione binomiale

    Consideriamo una situazione abbastanza simile a quella delle successive alzate di un mazzo di carte ( dipendenza e indipendenza):

lanciamo una moneta equa 10 volte;  qual è la legge di distribuzione della variabile casuale:  N = "n° di teste uscite"?

    Sembra un problema stupido, ma vedremo che è il punto di partenza per affrontare problemi più significativi, come:
un forno automatico produce mediamente 1 biscotto bruciacchiato ogni 8, e i biscotti sono successivamente mescolati e impacchettati automaticamente in confezioni da 6,
• qual è la probabilità che in una confezione non vi siano biscotti bruciacchiati, o che ve ne sia 1, …, o che siano tutti bruciacchiati?,
• cioè qual è la legge di distribuzione della variabile casuale N = "n° di biscotti bruciacchiati in una confezione" ?

    Proviamo prima a studiare il problema con una simulazione.  L'idea è generare 10 volte un numero a caso equamente distribuito tra 0 e 1, pensando 0 come "croce" e 1 come "testa", e prendere come N la somma di questi 10 numeri;  infatti tale somma è uguale a numero delle volte che è uscito 1, cioè "testa".

    Facciamo l'analisi con un semplice programmino in JavaScript. Vedi QUI.

n = 100000; x = new Array(11)
for(j=0; j<=10; j=j+1) x[j]=0
for(i=1; i<=n; i=i+1) { k=0
  for(j=0; j<10; j=j+1) if(Math.random()<0.5) k=k+1
  x[k]=x[k]+1 }
for(j=0; j<=10; j=j+1) document.write(x[j]/n+",")

Ottengo:

0.00107,0.00974,0.04505,0.11674,0.20511,0.24744,0.20414,0.11678,0.04326,0.00953,0.00114

Volessi le uscite in forma percentuale metterei x[j]/n*100:

0.107, 0.974, 4.505, 11.674, 20.511, 24.744, 20.414, 11.678, 4.326, 0.953, 0.114

    Posso tracciare l'istogramma con lo script "istogramma" (QUI):

0 1 2 3 4 5 6 7 8 9 10

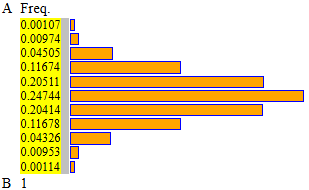i dati:   0*0.00107, 1*0.00974, 2*0.04505, 3*0.11674, 4*0.20511, 5*0.24744, 6*0.20414, 7*0.11678, 8*0.04326, 9*0.00953, 10*0.00114 A = -0.5   B = 10.5   11 intervalli media = 4.99325

    Effettuiamo, ora, lo studio teorico. Dobbiamo trovare i valori di Pr(N=0), Pr(N=1), ..., Pr(N=10).

    Iniziamo a considerare, per es., Pr(N=5).

•  Valutiamo la probabilità che testa esca esattamente nei primi 5 lanci (vedi figura a lato). La probabilità che esca T in un lancio è 1/2, la stessa che esca C. Poiché i dieci lanci sono indipendenti, posso moltiplicare le probabilità. Ottengo che la probabilità cercata è (1/2)·(1/2)·...·(1/2) = (1/2)10, cioè 2–10.
•  Ottengo lo stesso valore per la probabilità che testa esca nei lanci tra il 2° e il 6° (vedi figura a lato), e per qualunque altra collocazione dei 5 lanci in cui esce testa.
•  I modi in cui posso scegliere i 5 posti sono C(10,5), dove C(n,k) indica quante sono le combinazioni di n elementi k a k, cioè la quantità dei sottoinsiemi di k elementi di un insieme di n elementi ( calcolo combinatorio).
•  C(10,5) = 10/5 · 9/4 · 8/3 · 7/2 · 6/1 = 9·4·7
•  Quindi, la probabilità cercata, per la proprietà additiva, è la somma di C(10,5) termini uguali a 2–10:
Pr(N=5) = C(10,5) · 2-10 = 9·4·7 / 210 = 24.6%

In generale:

Pr(N = i) = C(10, i) / 210  (i = 0, 1, …, 10)

    Per controllare il nostro ragionamento teorico confrontiamoci con gli esiti della simulazione: dall'istogramma sperimentale abbiamo, ad es., Pr(N=5) = 24.7% e Pr(N=3) =11.7%; con la formula trovata per Pr(N=5) abbiamo ottenuto 24.6%; per Pr(N=3) abbiamo C(10,3) / 2¹⁰ = 10/3·9/2·8/1 / 2¹⁰ = 15 / 2⁷ = 11.7%. In entrambi i casi abbiamo un buon accordo.

  Se lanciassi n volte la moneta avrei, del tutto analogamente:

Pr(N = i) = C(n, i) / 2ⁿ  (i = 0, 1, …, n)

È un caso particolare di legge di distribuzione binomiale, discussa più in generale tra un paio di paragrafi. Il nome deriva dalla presenza del coefficiente binomiale C(n,i).

    Ecco, tracciati con questo e questo script, l'istogramma sprimentale (già visto, per 10 mila prove) e quello teorico nel cason = 10:  come si vede i due istogrammi praticamente coincidono.

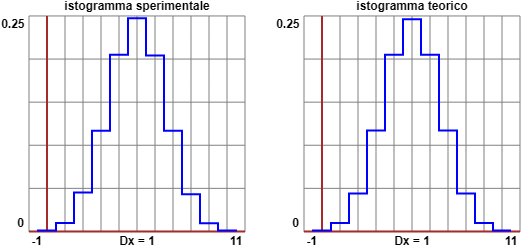
    Analizziamo sperimentalmente con 10 mila prove, con un programmino in Javascript analogo al precedente, il caso n = 9:

0 1 2 3 4 5 6 7 8 9

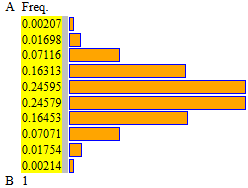i dati:   0*0.00207, 1*0.01698, 2*0.07116, 3*0.16313, 4*0.24595, 5*0.24579, 6*0.16453, 7*0.07071, 8*0.01754, 9*0.00214 A = -0.5   B = 9.5   10 intervalli media = 4.50317

    Vediamo come si potrebbero calcolare varianza e scarto quadratico medio, nel caso n=10, con un programmino e poi con la nostra "calcolatrice2". Ecco il programmino in JavaScript (vedi).

function Cbin(n,k) {if(k>n/2) k=n-k; CB=1; for(j=0;j<k;j=j+1) CB=CB*(n-j)/(k-j); return CB}
dato = new Array; freq = new Array; n = 10
ndati=0; for(i=0; i<=n; i=i+1) { dato[i]=i; freq[i]=Cbin(n,i); ndati=ndati+freq[i]}
for(i=0; i<=n; i=i+1) document.write(dato[i]+"*"+freq[i]+ " "); document.write("<br>")
tot=0; for(i=0; i<=n; i=i+1) tot=tot+dato[i]*freq[i]
media = tot/ndati
document.write("totale = " + tot + ", media = "+ media)
tot=0; for(i=0; i<=n; i=i+1) tot=tot+Math.pow(dato[i]-media, 2)*freq[i]
varianza = tot/ndati
document.write("<br>varianza = " + varianza)
document.write(", sqm = " + Math.sqrt(varianza))

    Uscite:

0*1 1*10 2*45 3*120 4*210 5*252 6*210 7*120 8*45 9*10 10*1
totale = 5120, media = 5
varianza = 2.5, sqm = 1.5811388300841898

    Con "calcolatrice 2" (vedi) basta semplicemente introdurre nel box riprodotto sotto "0*1, 1*10, 2*45, 3*120, 4*210, 5*252, 6*210, 7*120, 8*45, 9*10, 10*1" e cliccare [var] e [sqm]:

  La media, per simmetria, è evidentemente n/2. È naturale congetturare, da questi esempi in cui i calcoli sono stati effettuati dal computer, che la varianza sia n/4 (ho ottenuto 2.5 per n=10, 2.25 per n=9) e che, quindi, lo scarto quadratico medio sia σ = √n/2. La cosa può essere effettivamente dimostrata:

•  N = u₁ + u₂ + ... + u_n  dove per tutti gli u _k si ha u _k=1 se al primo lancio è uscita T, u _k=0 altrimenti.
•  i lanci sono indipendenti, quindi la "varianza della somma è la somma delle varianze";
•  M(u _k) = 1/2; Var(u _k) = 1/2 (0-1/2)² + 1/2 (1-1/2)² = 1/4; ...
•  Var(N) = Var(u₁) + ... + Var(u_n) = 1/4·n = n/4

  Torniamo all'esempio del forno, così sintetizzabile:

se un forno produce mediamente 1 biscotto bruciacchiato ogni 8, qual è la legge di distribuzione della variabile casuale  N = "n° di biscotti bruciacchiati in una confezione da 6".

    Ragioniamo in modo simile a quanto fatto nel caso delle monete.

    Sia N la variabile casuale a valori in {0, 1, ..., 6} che rappresenta il numero di biscotti difettosi.

    È sensato ritenere (dato il rimescolamento presente prima del confezionamento) che le estrazioni dei biscotti siano una indipendente dall'altra. Quindi la probabilità che esattamente i primi k biscotti estratti siano difettosi è data dal prodotto:

(1/8)·(1/8)· … ·(1/8)·(7/8)· … ·(7/8) = (1/8)^k·(7/8)^6-k.

	Poiché non ci interessa la disposizione dei biscotti difettosi, abbiamo: Pr(N=k) = C(6,k)·(1/8)k·(7/8)6–k.
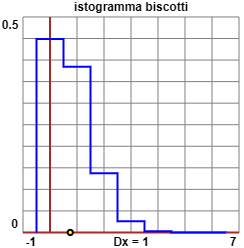
		Ecco, a sinistra, l'elaborazione grafica (ottenuta con questo script), che non è più simmetrica rispetto alla verticale passante per la media (segnata con un pallino),  e, sotto, i calcoli effettuati questo programmino:
		totale = 0.75 media = 0.75 varianza = 0.65625 sqm = 0.81009258730098255 Potevamo usare anche questi altri programmini

Qual è la probabilità che una confezione presenti biscotti bruciacchiati?

    Trovare la probabilità che vi sia almeno un biscotto difettoso vuol dire calcolare  Pr(N > 0), che (per la proprietà additiva) equivale a  100% – Pr(N = 0):

1 – C(6,0)·(1/8)⁰·(7/8)⁶ = 1 – 1·1·(7/8)¹⁰ = 1 – 0.4487953... = 55.1% [valore arrotondato]

  Generalizzando dal caso di una confezione da 6 ad una da n biscotti, dal caso della difettosità con probabilità di 1/8 a quello della difettosità con probabilità p, abbiamo che la probabilità che in una confezione vi siano k biscotti difettosi è:

 Pr(N = k) = C(n, k) · p^k · (1 – p)^n–k 

    Anche questa legge di distribuzione, che generalizza quella considerata nel caso delle monete eque, viene chiamata legge di distribuzione binomiale (o di Bernoulli).

Si applica a tutte le situazioni in cui si ripete n volte la prova su una variabile casuale che può assumere solo due valori, in cui p è la probabilità di uno di questi due valori e N è il numero delle volte in cui questo valore esce.

    Possiamo osservare, come già fatto per le monete, che N è interpretabile come  ∑ _iⁿ_{= 1} X _i  con X _i a valori in {0,1} e distribuzione: Pr(X _i=1) = p, Pr(X _i=0) = 1–p.  Da qui, tenendo conto che
• M(X _i) = Pr(X _i =0)·0+Pr(X _i =1)·1 = (1–p)·0+p·1 = p  e
• Var(X _i) = Pr(X _i =0)·(0–p)²+Pr(X _i =1)·(1–p)² = (1–p)p²+p(1–p)² = p(1–p)  abbiamo (vedi):

M(N) = M(Σ _i X _i) = Σ _i M(X _i) = p + … + p = np   e (vedi):

Var(N) = Var(Σ _i X _i) = Σ _i Var(X _i) = p(1-p) + … + p(1-p) = np(1–p).

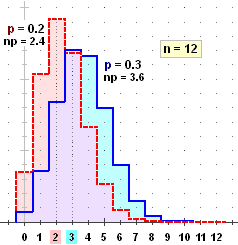
Nel caso dei biscotti: M(N) = 6·1/8 = 3/4,  Var(N) = 6·1/8·7/8 = 21/32 = 0.65625, in accordo coi valori calcolati direttamente sopra.       A lato la rappresentazione grafica di due leggi binomiali. Si noti che in entrambi i casi la media, np, differisce per meno di un'unità dalla moda (in un caso differisce di 0.6, nell'altro di 0.4).  Si può dimostrare che questo accade in generale, per ogni n naturale e per ogni p in (0,1).

Esercizio (e soluzione)

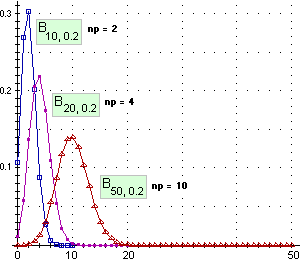
Il grafico della legge binomiale Bn, p di ordine n e "probabilità di successo nella singola prova" p quando n è molto grande, è pressoché simmetrico rispetto alla retta verticale che ha per ascissa la media, anche se p ≠ 1/2.     A lato sono raffigurati per p = 0.2 i casi n = 50, 20, 10 (i punti che rappresentano P(N=k) per k alto hanno ordinata trascurabile rispetto al punto modale, per cui appaiono confusi con l'asse orizzontale). Più n è piccolo, più è evidente la asimmetria, con una "coda" verso destra.

    Nelle situazioni in cui n è molto grande (si pensi a un problema di "pezzi difettosi", come quello dei biscotti, nel caso si debba valutarne la presenza in una partita di 1000 pezzi), il calcolo dei coefficienti binomiali diventa molto complicato. Vedremo, in una voce successiva [ limiti in probabilità], che all'aumentare di n i grafici delle leggi binomiali tendono a stabilizzarsi sul grafico di una funzione rappresentata da una formula determinabile a partire da n e p. Questo semplificherà notevolmente lo studio di tali situazioni.

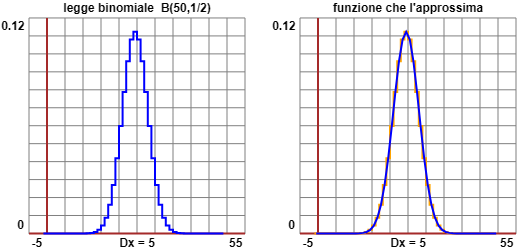
    Sotto è raffigurato il caso di B_50,1/2, da cui si capisce che tale funzione avrà grafico simmetrico rispetto alla retta verticale avente come ascissa il valor medio.

Altri esercizi:     uno   soluz.,     due   soluz.