Correlazione tra variabili casuali

  Covarianza e correlazione

    Alla voce sistemi di variabili casuali abbiamo visto esempi di variabili X e Y, come ascissa e ordinata dei punti di un bersaglio che vengono colpiti, che non sono stocasticamente indipendenti ma che, tuttavia, danno luogo a un diagramma di dispersione in cui non viene privilegiata alcuna direzione, e altri, alla fine della voce, in cui i punti tendono a disporsi lungo una linea obliqua, ossia in cui, all'aumentare di X, Y tende ad aumentare più o meno proporzionalmente.  Per distinguere queste situazioni, in entrambe delle quali X e Y sono dipendenti, si dice che X e Y nel secondo caso sono correlate, nel primo no.

    Per "misurare" la tendenza delle due variabili a variare proporzionalmente si usa il concetto di covarianza, che deriva il suo nome dalla parentela con la formula della varianza:  al posto del quadrato dello scarto di una variabile si prende il prodotto dei due scarti:

    Var(X) = M( (X-M(X))² )

    Var(Y) = M( (Y-M(Y))² )     covarianza:   Cov(X,Y) = M( (X-M(X))·(Y-M(Y)) )

    Nel caso sperimentale, se m_x e m_y sono le medie di X₁,…,X_n e di Y₁,…,Y_n  (ovvero le coordinate del baricentro: leggi di distribuzione),  questo termine diventa:

    La formula  Σ _i=1..n (X_i - m_x)·(Y_i - m_y) / n  per calcolare la covarianza, come spiegato sopra, rappresenta un indicatore che assume un valore assoluto che scende quanto più i punti tendono a disporsi in modo da presentare una simmetria verticale o orizzontale e che cresce quanto più i punti tendono a disporsi lungo una retta obliqua.

    Per non tener conto delle unità di misura in cui sono espressi X e Y (e per passare da un'"area" a un numero puro) la covarianza viene normalizzata dividendo per gli s.q.m. di X e Y, introducendo il:

coefficiente di correlazione:  r X,Y  =

Cov(X,Y) ————— √(V(X) V(Y))

=

Cov(X,Y) ——————— sqm(X)·sqm(Y)

    L'interpretazione geometrica considerata sopra fa supporre che se X e Y sono dipendenti deterministicamente e legate da una relazione lineare  Y = aX + b  il coefficiente di correlazione assuma valore assoluto massimo. Ciò può effettivamente essere dimostrato (la dimostrazione non è complicata, ma la omettiamo).
    Si ricava facilmente, usando le proprietà della media, che in questo caso r _X,Y = sgn(a)  [sgn(a) = 1 se a>0, sgn(a) = 1 se a<0  –  vedi].
    Quindi, in generale,  1 ≤ r _X,Y ≤ 1.

Nota. Come abbiamo visto alla voce limiti in probabilità, "sqm" può essere stimato usando come denominatore "n−1" invece che "n".  Una cosa analoga accade per la covarianza. Dato che il coefficiente di correlazione si ottiene come rapporto in cui compaiono a numeratore e a denominatore covarianza e "sqm", per esso non ci sono ambiguità: sia in un caso che nell'altro si ottiene lo stesso valore.

    Per rendere più semplice il calcolo del coefficiente di correlazione si piò ricorrere qui allo script "retta regressione" che, oltre a calcolare tale valore, individua anche la "retta di regressione", ossia la retta che meglio approssima i dati, su cui ci soffermeremo nei prossimi paragrafi.  Ecco, sotto, che cosa si deve fare per studiare la relazione tra X = (10, 20, 30, 40) e Y = (30, 40, 50, 60):

    Lo script in questo caso fornisce come coefficiente di correlazione ovviamente 1 in quanto i punti sono esattamente allineati.

Grafico realizzato con questo script  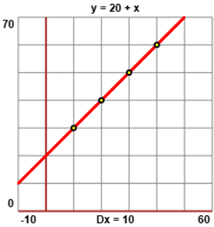→       Esercizio 1     soluzione

  Un esempio. Limiti e usi distorti della correlazione.

    A questo punto proviamo ad analizzare coppie (e n-uple) di variabili casuali.  Come nel caso "univariato", i dati possono essere introdotti direttamente o essere letti da file, in cui le "colonne" indicano i soggetti su cui si è effettuato il rilevamento e le "righe" indicano le variabili casuali (o modalità) rilevate.

    Ecco, ad esempio, la parte iniziale del file battito.htm:

Indagine sugli studenti (92) di un corso universitario, dal manuale di MiniTab
# numerazione degli studenti:       1, 2, 3, ..., 92
# battiti prima di eventuale corsa di 1 min:       64, 58, 62, ..., 76
# battiti dopo:       88, 70, 76, ..., 76
# fatta corsa (1 sì; 0 no; a seconda di esito di lancio moneta):       1, 1, 1, ..., 0
# fumatore (1 sì; 0 no):       0, 0, 1, ..., 0
# sesso (1 M; 2 F):       1, 1, 1, ..., 2
# altezza (cm):       168, 183, 186, ..., 156
# peso (kg):       64, 66, 73, ..., 49
# attività fisica (0 nulla;1 poca;2 media; 3 molta):       2, 2, 3, ..., 2

    Se raccolti su un foglio di calcolo i dati assumerebbero l'aspetto seguente, ma noi analizzeremo i dati con dei programmini più semplici e più efficienti di un "foglio di calcolo":

battito	64	58	62	...
battito dopo corsa	88	70	76	...
fatta corsa	1	1	1	...
...	...	...	...	...

    I dati sono stati rilevati durante una lezione di un corso universitario (almeno così viene detto in un manuale del software statistico MiniTab da cui essi sono stati tratti e parzialmente rielaborati per presentarli nel sistema metrico decimale).  La riga "battiti dopo" si riferisce a un secondo rilevamento del battito cardiaco effettuato dopo che gli studenti a cui (lanciando una moneta) è uscito testa (1 nella colonna "corsa") hanno fatto una corsa di un minuto.

    Uno strumento che ci serve, evidentemente, è quello che ci consenta estarre da una tabella i dati che soddisfino certe condizioni, ad esempio estrarre i dati realtivi alla altezza delle femmine.  Lo script è "sottosequenza" presente qui.  Ecco come usarlo:

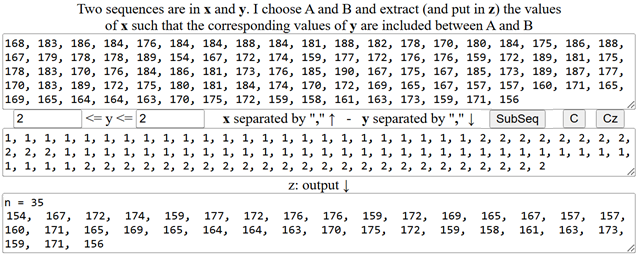
    Ho messo in "x" le altezze, in "y" le codifiche dei sessi e ho selezionato con 2≤y≤2 il sesso femminile.

n = 35     154, 167, 172, 174, 159, 177, 172, 176, 176, 159, 172, 169, 165, 167, 157, 157, 160, 171, 165, 169, 165, 164, 164, 163, 170, 175, 172, 159, 158, 161, 163, 173, 159, 171, 156

    Analogamente ottengo le altezze dei maschi:

n = 57     168, 183, 186, 184, 176, 184, 184, 188, 184, 181, 188, 182, 178, 170, 180, 184, 175, 186, 188, 167, 179, 178, 178, 189, 189, 181, 175, 178, 183, 170, 176, 184, 186, 181, 173, 176, 185, 190, 167, 175, 167, 185, 173, 189, 187, 177, 170, 183, 189, 172, 175, 180, 181, 184, 174, 170, 172

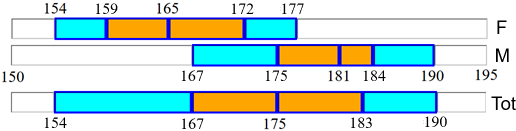
    Posso confrontrare i dati in molti modi. Ad esempio con lo script "calcolatrice2" posso calcolare le medie (femmine: 166.03 cm, maschi: 174.43 cm, totale: 179.60 cm), le mediane, gli sqm, ...,  con "box-plot" posso tracciare i boxplot e, poi, con "box-plot cl", utilizzando i valori ottenuti (25º, 50º e 75º percentile), posso tracciare i box-plot usando la stessa scala, in modo da confrontarli.  Sono evidenziate in modo efficace le differenze tra maschi e femmine:

    Posso pure tracciare gli stogrammi, con lo script "istogramma":

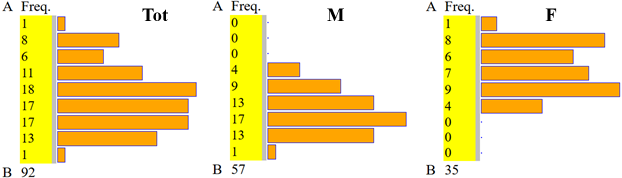
    Lasciamo come esercizio studiare le altre variabili.  Vediamo come studiare le relazioni tra una variabile e l'altra.

    Possiamo usare nuovamente lo script "retta regressione". Confrontiamo ad esempio le variabili altezza e sesso (1: M, 2: F):

    Si ottiene -0.7090, molto vicino a -1, a conferma che i maschi sono in genere più alti.

    Analizzo analogamente la realzione tra altezza e peso.  Ottengo 0.7826.  Un valore molto alto.  Se ci restringiamo a una sottopopolazione più omogenea (quella femminile o quella maschile, che hanno pesi e altezze con medie abbastanza diverse), mi potrei aspettare di ottenere un coefficiente maggiore.  Ma se, dopo aver rappresentato graficamente la relazione tra altezza e peso, estraggo i maschi e estraggo le femmine, e rappresento la relazione anche in questi due casi ottengo:

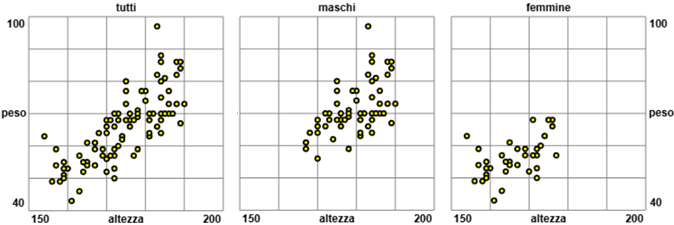
Capisco che la forma allungata dell'insieme dei punti relativi all'intero campione è dovuta all'unione di due "nuvole" (quella dei maschi e quella delle femmine) centrate sui rispettivi baricentri.     Se congiungo i due baricentri ottengo una retta inclinata che passa più o meno in mezzo ai punti →     Determinando i coefficienti di correlazione nei due casi trovo effettivamente numeri in valore assoluto più bassi di 0.7090:  per i maschi 0.590, per le femmine 0.519. [Vedi QUI per gli script con cui sono stati realizzati i grafici precedenti]     Questo esempio mette in luce come le statistiche che si ottengono sono spesso ingannevoli.  In casi come questo, abbastanza frequenti, il problema è dovuto alla presenza di due sottopopolazioni con caratteristiche differenti.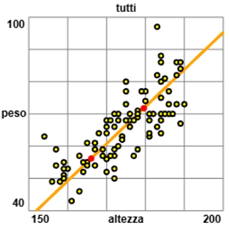

    Poi, come già osservato ( vedi), introducendo i concetti probabilistici, occorre tener conto che quelle individuate sono solo relazioni statistiche, non di causa-effetto.  Ad esempio nel caso della correlazione tra le colonne "battito dopo" e "corsa" di "battito" (che vale 0.5768), c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco).  Ma quando nel caso di uno studio statistico sulle condizioni delle famiglie è emersa una forte correlazione negativa fra il loro consumo di patate e la superficie dell'abitazione in cui vivono, essa non è da interpretare come conseguenza di una relazione di causa-effetto:  è semplicemente dovuta al fatto che le famiglie benestanti abitano in genere in case di maggiori dimensioni e, nello stesso tempo, consumano meno patate delle altre famiglie privilegiando cibi più costosi, come la carne e il pesce.  Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.

Osserviamo, infine, che il coefficiente di correlazione è rilevante se i dati sono molti; basti pensare che avere tre punti più o meno allineati ha senz'altro un significato diverso dall'averne molti.

Esercizio 2    soluzione           Esercizio 3    soluzione
 

  Rette di regressione

    Di fronte a dati sperimentali relativi a un sistema (X,Y) per cui si ritiene che Y vari in funzione di X, si può cercare di trovare una funzione F tale che il suo grafico approssimi i punti sperimentali.  In curve approssimanti questo problema è affrontato nel caso in cui X sia una variabile deterministica.  È simile il modo in cui si affronta il caso in cui X sia casuale.

    In base ai dati (con una delle tecniche viste in curve approssimanti) e, possibilmente, in base a considerazioni teoriche, si cerca di individuare il tipo di funzione (lineare, polinomiale, esponenziale, ) che si vuole utilizzare.  Se si ipotizza che ci sia una relazione lineare che esprima Y in funzione di X, e non si hanno altre informazioni, la tecnica in genere usata è quella dei minimi quadrati  (già impiegata per introdurre la variabile χ²).  Illustriamola su un semplice esempio.

Voglio approssimare la relazione tra due variabili casuali G1 e G2 con una relazione del tipo G2 = k G1. Devo determinare k. In tre esperimenti ottengo le coppie (G1,G2) rappresentate a lato con i punti A, B e C. Per determinare k decido di cercare, tra tutti i grafici del tipo G2 = k G1 (rette passanti per l'origine) come quello raffigurato a fianco, il grafico che rende minima la somma dei quadrati degli scarti tra i valori di G2 sperimentali e quelli che sarebbero stati associati ai valori G1 dalla relazione G2 = k G1. Ossia cerco la pendenza k che deve avere una retta passante per l'origine affinché la somma dei quadrati di a, b e c (vedi fig. a lato) sia minima. a = |yA - k xA|, b = |yB - k xB|, c = |yC - k xC|. a2+ b2+ c2 = (k xA - yA)2+ (k xB - yB)2+ (k xC - yC)2.     È un'espressione polinomiale in k di secondo grado. Assume valore minimo quando si annulla la sua derivata rispetto a k, ossia quando: 2(k xA - yA)xA + 2(k xB - yB)xB + 2(k xC - yC)xC = 0 ossia:  k = (xAyA+ xByB+ xCyC)/(xA2 + xB2 + xC2)     In questo caso (1.6*18+3.6*26+4.8*48)/(1.6*1.6+3.6*3.6+4.8*4.8) = 9.14937759...

    Comunque, per fare prima, e ridurre la possibilità di commettere errori, possiamo ricorrere ancora allo script "retta regressione".  Se i punti sono (1.6,18), (3.6,26), (4.8,48),  imponendo che la retta passi per (0,0),  trovo y = 9.1494*x.

Un esempio concreto. Consideriamo le distanze chilometriche da Genova in linea d'aria e lungo la strada di alcune città italiane del centro-nord (a lato è tracciato il grafico di dispersione). DA:   55,  70, 155, 160, 155, 115, 105, 165, 110, 115,  85, 165, 110, 155, 105 DS:  85, 115, 205, 230, 185, 185, 145, 240, 140, 155, 125, 290, 170, 195, 135     Prima di analizzare i dati cerchiamo di congetturare con un ragionamento teorico come potrebbe essere fatta una funzione che approssimi la relazione tra DS e DA:  la distanza lungo la strada sicuramente è maggiore di quella in linea d'aria;  supposto di essere in una regione dalle caratteristiche geografiche non molto diversificate e che non presenti territori invalicabili  (a causa di catene montuose a picco, di insenature o laghi molto grandi)  essa dovrebbe crescere più o meno proporzionalmente alla distanza in linea d'aria;  per stimare il rapporto tra l'una e l'altra, tenendo conto delle curve supponiamo che esso sia circa pari al rapporto che c'è tra la strada per raggiungere due vertici opposti di un quadrato passando per il bordo o la strada diretta, cioè √2 = 1.4 circa.     Se studio i dati con lo script "retta regressione":

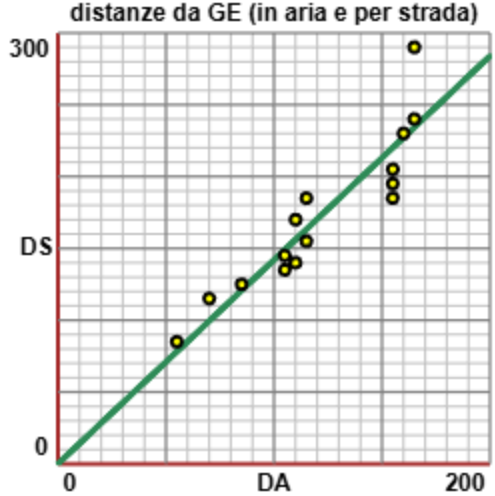trovo che c'è un alto coeff. di correlazione (0.91) tra DA e DS e che la retta y = a x che approssima (col metodo dei minimi quadrati) i dati ha a = 1.42046, in accordo con la nostra stima teorica.
    La figura precedente è stata realizzata con questo script.

Esercizio 4     soluzione         Esercizio 5     soluzione
 

Alla voce sistemi di variabili casuali abbiamo considerato i punti di arrivo dei proiettili che cadono con distribuzione uniforme in un bersaglio circolare, come raffigurato nella figura a destra.     Come sarà la retta di regressione di questi punti?     Prima si riflettere teoricamente sulla cosa, studiamo il fenomeno sperimentalmente.  Generiamo 200 punti che cadono in questo modo e poi li analizziamo.  Generiamo i punti con un programmino in JavaScript: n = 200; m=0 X = new Array(n); Y = new Array(n) for(i=1; i <= n*2; i=i+1) {x=Math.random()*2-1; y=Math.random()*2-1 if(x*x+y*y<1) {m=m+1; X[m]=x; Y[m]=y; if(m==n) {i=n*2}} } for(i=1; i<=n; i=i+1) {document.write( X[i]+", ") } document.write("<br>"+n+"<br>") for(i=1; i<=n; i=i+1) {document.write( Y[i]+", ") }

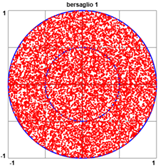[genero 400 x e y tra -1 ed 1 e metto nelle sequenze X ed Y solo i primi 200 che rappresentino
punti del cerchio di centro (0,0) e raggio 1; poi stampo le due sequenze, separate dal numero 200]

    Analizzandoli con "retta regressione" ottengo:

    Praticamente, come ci aspettavamo, il baricentro è (0,0) e il coefficiente di correlazione è 0.  La retta di regressione è y = 0.  Come mai?

    Ci saremmo potuti aspettare anche, per esempio, y = x?  Per dare una risposta riflettiamo sull'esempio di questi 4 punti diposti simmetricamente rispetto agli assi:  (1,1), (1,-1), (-1,1), (-1,-1).

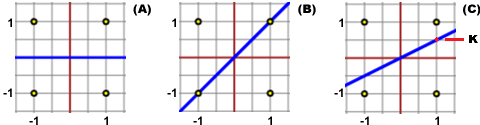
    Quale delle tre rette (y=0, y=x, y=K·x) rende minima la somma dei quadrati delle distanze da essa dei quattro punti?
(A):  1+1+1+1 = 4;  (B):  0+4+4+0 = 8;  (C):  (1-K)²+(1+K)²+(1+K)²+(1-K)² = 2((1-K)²+(1+K)² = 2(2+2·K²) = 4+4·K²

    È evidente che il minimo lo si ha nel caso (A), ovvero nel caso (C) quando K = 0!

    Pensando a questi esempi è facile concludere anche che, mentre la correlazione non dipende dall'ordine con cui scelgo le due sequenze (X e Y), nel caso delle regressione (tranne quando i punti sono pefettamente allineati) a seconda della scelta si ottengono valori diversi.

È possibile tracciare anche la retta che "meglio approssima" i punti quando lo scarto da essi sia misurato con la sommatoria dei quadrati delle distanze dei punti sperimentali dalla retta  (le rette di regressione sono invece ottenute considerando non le distanze, ma le loro proiezioni, orizzontali o verticali).  Questo si ottiene chiedendo il tracciamento degli assi principali di dispersione:  si tratta di due rette perpendicolari, passanti anch'esse per il baricentro, chiamate così perché per alcune elaborazioni statistiche vengono assunte come nuovo sistema di riferimento (per facilitare calcoli e forme di ragionamento).  Esse corrispondono agli assi di simmetria delle curve di livello della superficie considerata nella voce sistemi di variabili casuali.     Nella figura qui a destra sono raffigurati alcuni punti sperimentali e, in verde, la retta di regressione.  In rosso sono rappresentati gli assi principali.

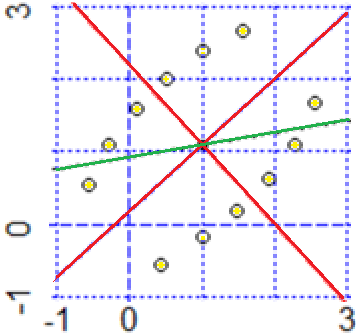
Ancora un esempio     Alla voce limiti in probabilità abbiamo considerato le altezze e i pesi rilevati alle visite di leva per la Marina del 1997 (primi scaglioni).  Consideriamo anche la circonferenza toracica (in cm):  vedi.     A destra è raffigurato l'insieme delle coppie (torace, peso), con rappresentata anche (in colore blu) la retta di regressione torace → peso e (in colore verde) la retta di regressione peso → torace, che, come abbiamo ricordato due paragrafi fa, non coincidono a meno che i punti non siano perfettamente allineati.     Le due rette si intersecano nel centroide, o baricentro (segnato in colore giallo).  Quanto più è ampio l'angolo formato dalle due rette di regressione (a parità della scala di rappresentazione) tanto più le due variabili sono "scorrelate".     Ovviamente, essendo migliaia di punti, molti di essi, vicini al centroide, si sovrappongono.     Ricordiamo che gli istogrammi dei pesi e del torace, a differenza del caso delle altezze, non hanno affatto una forma gaussiana: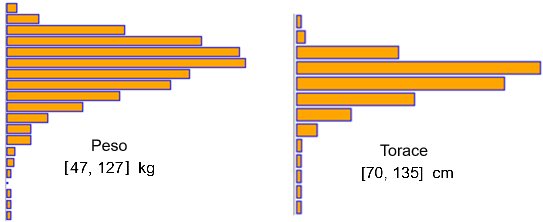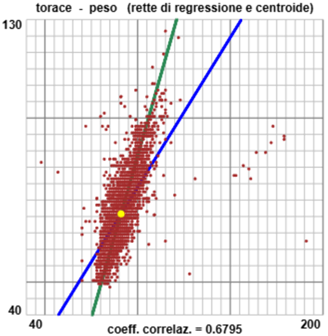

    Vedi qui se vuoi vedere come è stato tracciato il grafico torace-peso precedente.

  Un esempio di analisi di dati sperimentali (Grandezza1 in funzione di Grandezza2)

    Consideriamo un esempio relativo a dati dotati di precisione.

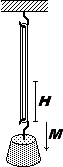Per studiare le caratteristiche di un elastico, lo si tiene sospeso per un estremo e si appendono all'altro estremo diversi oggetti. Ogni volta si misura il peso dell'oggetto e il corrispondente allungamento dell'elastico.     Il peso F degli oggetti viene misurato con una bilancia a molla con divisioni di 10 g (in modo che se l'ago si ferma vicino alla tacca 220 si può assumere che il peso sia 220±5 g).  Le lunghezze che assume l'elastico vengono misurate con la precisione di 1 mm, in modo che i valori dell'allungamento H (ottenuti come differenza di due lunghezze) hanno la precisione di 2 mm.  Si ottengono i valori riportati nella tabella a fianco.     I valori sono stati rappresentati anche su un grafico, con dei pallini.  Evidentemente H ed M sono correlate:  al variare dell'una anche l'altra tende a variare più o meno proporzionalmente.  Per misurare quanto i punti che rappresentano le due variabili casuali tendono a disporsi lungo una retta obliqua  (passante o no per l'origine)  si usa il coefficiente di correlazione  (vicino a 0 se le variabili sono poco correlate, ad 1 se i punti sono quasi allineati lungo una retta con pendenza positiva, a -1 se sono quasi allineati lungo una retta con pendenza negativa).

H (mm) F (g) 15 260 20 380 39 710 52 990

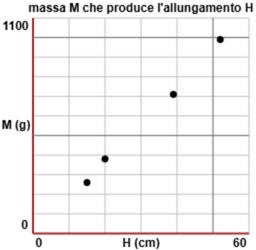    Con lo script "retta regressione" (qui) mettendo:   x:  15, 20, 39, 52       P:  0 | 0        y:  260, 380, 710, 990
ottengo:     y  =  18.694845360824743 x + 0         correlation coefficient   0.9987686248984358

    Sotto a sinistra la rappresentazione della retta di regressione e dei punti sperimentali (H,M).  In questo caso essi non li ho rappresentati con dei pallini in quanto di H e di M non conosco solo dei valori approssimativi ma conosco le misure approssimate e le relative precisioni, di 2 (mm) e di 5 (g):  quindi ho rappresentato correttamente i punti sperimentali con dei rettangolini di base 4 e altezza 10.

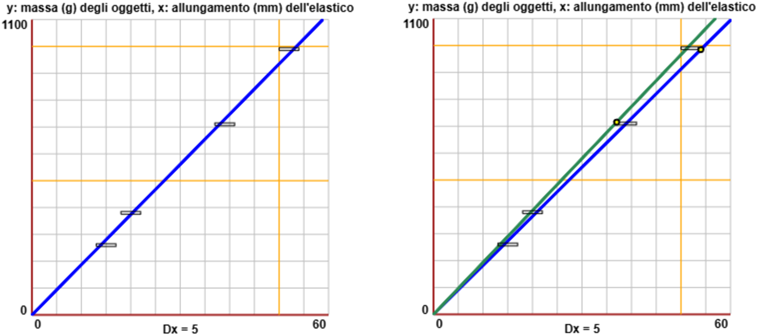
    Ma la retta è stata tracciata tenendo conto solo dei valori di H e di M, senza utilizzare le informazioni sulle loro precisioni!  Devo cercare le rette passanti per l'origine e per i tutti i rettangolini di minima e di massima pendenza, come fatto nella figura sopra a destra.  La prima ha pendenza (710+5)/(39-2) = 715/37 = 19.32432432..., la seconda (990-5)/(52+2) = 985/54 = 18.24074074...  Quindi la relazione è  M = k·H  (M in g, H in mm)  con k tra 18.24 e 19.33, ovvero tra 18.2 e 19.4, ovvero  k = 18.8 ± 0.6.

    Gli script con cui sono stati tracciati i grafici precedenti sono questo e questo.

    Se non avessimo avuto informazioni sulle precisioni (ovvero avessimo rappresentato dei dati con dei pallini) alla retta di regressione avremmo dovuto comunque associare una precisione che tenesse conto sia dei valori dei dati che della loro quantità. Vi sono degli oggetti matematici (gli "intervalli di confidenza") che consentono di fare queste valutazioni, ma che (negli studi preuniversitari) non siamo in grado di affrontare.  Osserviamo solo che nel caso di questo problema avremmo ottenuto che il rapporto M/H, che sopra abbiamo essere compreso tra 18.2 e 19.4, è "con probabilità del 90%" compreso tra 17.73 e 19.06.  L'intervallo [17.73, 19.06] è chiamato intervallo di confidenza al 90% di M/H. Per qualche informazione in più puoi cercare in WolframAlpha "confidence interval".

  Relazioni non lineari

    Sopra abbiamo visto solo come approssimare coppie di dati con funzioni lineari.  Se i dati hanno andamento diverso occorre approssimarli con funzioni di tipo diverso, ma non disponiamo degli strumenti matematici per affrontare questo studio.  Facciamo solo qualche cenno al caso dei dati con andamento quadratico e cubico, solo per dare un'idea delle tecniche che si possono impiegare.

    Consideriamo un esempio semplice, che, comunque, si riferisce a situazioni abbastanza diffuse.
    Un oggetto, pesante e di forma compatta, viene lasciato cadere e ne viene misurata, mediante una successione di immagini fotografiche scattate ogni decimo di secondo, l'altezza in cm da terra.  Supponiamo che in corrispondenza dei tempi di 1, 2, 3, 5 decimi di secondo (rilevati con errori trascurabili) si registrino, in ordine, le altezze da terra di 131, 113, 89 e 7 centimetri, arrotondate tutte con la stessa precisione, ad esempio di 1 centimetro.

    In situazioni di questo tipo, in cui conosco le coordinate di N punti sperimentali con ascisse x_i note esattamente e con ordinate y_i della stessa indeterminazione, posso ricorrere ad un procedimento che impiega tecniche probabilistiche di vario tipo  (simili a quelle considerate per trovare le rette di regressione, e che rientrano nella cosiddetta "regressione polinomiale"),  per arrivare alla determinazione dei coefficienti della funzione polinomiale di grado 2 che "con maggiore probabilità" approssima i punti noti.
    Senza entrare nei dettagli di esso, si ottiene che si tratta della funzione F: x → A + B·x + C·x² dove A, B e C sono le soluzioni del sistema seguente:
    A·N + B·Σx_i + C·Σx_i² = Σy_i
    A·Σx_i + B·Σx_i² + C·Σx_i³ = Σx_iy_i
    A·Σx_i² + B·Σx_i³ + C·Σx_i⁴ = Σx_i²y_i.

    Tornando all'esempio, risolvendo il sistema (ad esempio con lo script "sistemi equazioni"):

trovo le soluzioni A = 173.3, B = -1.9455, C = -4.81818

    Ma posso trovare molto più semplicemente le soluzioni con lo script "regressione quadratica":

    Ecco sotto a sinistra il grafico della soluzione:

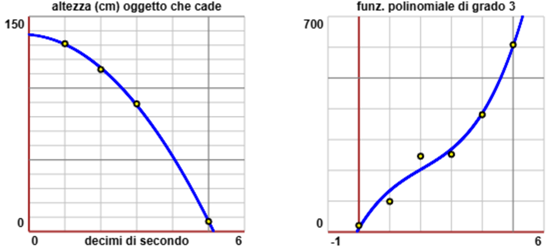
    Con un procedimento simile si può trovare la funzione polinomiale di grado 3 che approssima i punti di ascisse 0, 1, 2, 3, 4, 5 e ordinate 21, 99, 246, 252, 381, 608.  Con lo script "regressione cubica", si ottiene la funzione x → A + B·x + C·x² + D·x³: con A = 11.36508, B = 166.9709, C = -53.05159, D = 8.675926, rappresentata graficamente sopra a destra.

  Approfondimenti li puoi trovare in WolframAlpha, cercando mathworld subject multivariate statistics.  Esistono molte altre tecniche per analizzare forme di collegamento tra dati di vario genere. Una particolarmente usata è la cluster analysis, di cui cercando cluster analysis, puoi avere qualche cenno.
 

Esercizio 6    soluzione        Esercizio 7    soluzione        Esercizio 8    soluzione