Ancora su derivate e integrali

  Nella scheda  l'integrazione abbiamo introdotto il concetto di "integrazione" e abbiamo messo a fuoco la sua sostanziale equivalenza a quello di "antiderivazione".  In questa scheda prima svolgeremo alcune considerazioni storiche sulla derivazione e l'integrazione, affrontabili in tutti i tipi di scuola.  Poi approfondiremo la discussione di alcune difficoltà dell'integrazione, con riferimenti ad alcuni particolari insiemi di funzioni.

  Qualche richiamo storico

    Le origini del concetto di integrazione sono molto antiche.  Vari metodi per il calcolo esatto di aree di particolari figure a contorno curvilineo basati sulla loro approssimazione mediante figure poligonali erano già note alcuni secoli a.C. (Eudosso, Archimede, …).  Furono poi estese ad altre figure, grazie ad una prima introduzione delle coordinate, da Oresme, intorno al 1350 e, successivamente, da altri studiosi, tra cui Galileo, Torricelli e Cavalieri  (sono tutte persone che non erano dei matematici di professione, ma si occupavano di filosofia, tecnica, economia, scienze, arte, …: la matematica come disciplina autonoma risale al XIX secolo).

    L'idea del concetto di derivazione risale invece a Galileo Galilei, che mise a punto, attorno al 1600, le leggi matematiche che descrivono il movimento di un oggetto in caduta libera e il legame tra accelerazione, velocità e posizione dell'oggetto in funzione del tempo trascorso.  La formalizzazione del concetto di derivata, e la scoperta della formula fondamentale del calcolo, sono dovute, intorno al 1670, più o meno contemporaneamente, a Newton e Leibniz.

    L'area della matematica che si occupa dello studio delle proprietà e delle applicazioni del concetto di derivata si chiama calcolo differenziale.  L'area più generale che si occupa delle funzioni, del concetto di limite e degli altri concetti ad esso collegati (oltre alle derivate, i metodi per calcolare lunghezze, aree e volumi di figure definite mediante funzioni od equazioni, le proprietà delle funzioni continue, …) viene chiamata analisi matematica.  Spesso l'aggettivo analitico, in matematica, viene usato per indicare metodi in cui un oggetto o una proprietà viene studiata usando tecniche di analisi matematica.  In particolare lo studio delle figure mediante il ricorso alle funzioni od equazioni che le hanno per grafici viene a volte chiamato geometria analitica  (è una terminologia introdotta nei primi anni del XIX secolo per distinguerla dall'approccio alla geometria allora più diffuso, in cui lo studio delle figure era basato su metodi, più direttamente legati alla immediata intuizione fisica, che non ricorrevano ai numeri reali e alle funzioni).

  L'integrazione di alcune classi di funzioni

    Se derivo o integro una funzione polinomiale ottengo ancora una funzione polinomiale.
Ad es. se F(x) = 3x²+x−3√2  ho che  F'(x) = 6x+1  e che  ∫ F(x) dx = x³+x²/2−3√2x+c, al variare di c in R.
    Consideriamo le cosiddette funzioni razionali, ossia esprimibili cone rapporto tra due funzioni polinomiali.  La derivata di una di esse è ancora una funzione razionale, come conseguenza immediata delle regola per la derivazione del rapporto di due funzioni.  Ma l'integrazione di una funzione razionale non è detto che sia tale.  Ad esempio l'integrale rispetto ad x di 1/x è log(x), o log(−x), che non sono razionali.
[In qualche libro di testo le funzioni razionali che sono rapporto tra due funzioni polinomiali di primo grado vengono chiamate (a sproposito, e, a questo livello, in modo non comprensibile) funzioni omografiche. Il termine corretto è trasformazione lineare fratta (linear fractional transformation, in sigla LFT). Le omografie si occupano di questioni più generali, che qui non possiamo trattare]

    Di fronte a una funzione espressa mediante una formula usuale siamo sempre in grado di esprimerne mediante una formula la derivata e l'integrale?  Dobbiamo precisare che cosa intendiamo per "formula usuale":  se chiamiamo funzioni elementari le funzioni ottenibili mediante successive composizioni di funzioni polinomiali,  di elevamento a potenza, esponenziali, logaritmiche, circolari e circolari inverse, la risposta è positiva per la derivazione (abbiamo visto tutti i procedimenti per derivare una funzione elementare ottenendo una funzione elementare),  ma è negativa per l'integrazione.
    Ad es. so che  d (1/√(x⁴+1) / dx = −2x³/√((x⁴+1)³);  infatti la composizione di x → u = x⁴+1, u → y = u^−1/2 ha come derivata dy/dx = dy/du·du/dx = −1/2u^−3/2·4x³ = −2x³/√(u³).  Ma non si riesce a trovare un termine descritto mediante le usuali funzioni che sia uguale a  ∫ (1/√(1+x⁴) dx.
    Un altro esempio: di fronte a F(x) = e^x2 - che sta per e^(x^2) ovvero exp(x²) - so che F'(x) = 2x e^x2 ma non riesco a trovare alcuna funzione elementare la cui derivata sia F(x). Qualche altro esempio di funzioni, espresse con x come variabile di input, che sono nelle stesse condizioni:  √(x³+1), sin(x²), cos(e^x), sin(x)/x, e^x/x, 1/log(x).  In effetti solo una piccola minoranza delle funzioni elementari ha antiderivata elementare.

Nota. In altre parole, le funzioni elementari non sono altro che le F tali che F(x) può essere espresso con un termine in cui appaiono, applicati direttamente o indirettamente a x, solo i simboli log, exp, sin, cos, tan, arcsin, ..., oltre a quelli di somma, prodotto ed elevamento a potenza (e quelli di divisione e di estrazione di radice, che sono un caso particolare di elevamento a potenza).
Un esempio di funzione non elementare che studierai è la funzione di ripartizione della gaussiana.  Un altro esempio è la funzione n → n! (che è non elementare in quanto coinvolge una quantità di operazioni che cresce con n).

Esercizio   (e  soluzione)

    Si parla anche di funzioni algebriche per indicare quelle ottenibili componendo funzioni razionali ed estrazioni di radici (non solo quadrate), e, più in generale, ogni funzione che sia esprimibile come soluzione di una equazione polinomiale (come la funzione F dell'esempio seguente).
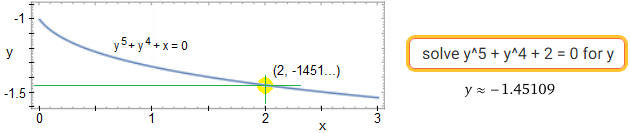
Ad esempio  y = (x - 1)^2/3+ k,  che equivale a  y = ³√((x - 1)²) + k,  esprime y come funzione algebrica di x, mentre  y = sin(k x²)  no, in quanto compare la funzione seno applicata a k x².  Un esempio più complesso è la funzione F tale che  F(x)⁵+F(x)⁴+x = 0,  che non è esplicitabile in forma elementare (ciò non toglie che si possa trovare dato x il valore di F(x) con una approssimazione buona quanto si voglia).

Esercizio   (e  soluzione)

    Si parla anche di funzioni trascendenti per indicare le funzioni non algebriche.  Sono tali, ad esempio, le funzioni trigonometriche e le esponenziali.

    Il software di calcolo simbolico ogni tanto esprime gli integrali usando simboli di funzione come sinh e cosh. Queste funzioni sono chiamate rispettivamente seno iperbolico e coseno iperbolico in quanto, in modo abbastanza simile alle funzioni seno e coseno, hanno la caratteristica che D(sinh) = cosh e D(cosh)= sinh. Inoltre, così come la curva x=cos(t), y=sin(t) al variare di t è un cerchio, così la curva x=cosh(t), y=sinh(t) al variare di t è un ramo di iperbole avente le bisettrici dei quadranti come asintoti.  Si ha che  sinh(x) = (exp(x)-exp(-x))/2  e che  cosh(x) = (exp(x)+exp(-x))/2.  Vedi qui.

    Su alcune particolari tecniche che possono essere utili per calcolare alcuni integrali si tornerà alla voce  calcolo di integrali.

  Numeri trascendenti
    Gli aggettivi trascendente e algebrico sono usati, in matematica, anche con altri significati, che val la pena di richiamare:  si dice (circa dal 1750) trascendente un numero (reale o complesso) che non è soluzione di alcuna equazione polinomiale a coefficienti interi; si dice algebrico un numero (reale o complesso) che non è trascendente, ovvero che è soluzione di qualche equazione polinomiale a coefficienti interi.  Si può provare che π e che e, oltre ad essere irrazionali, sono trascendenti. Le dimostrazioni sono recenti, rispettivamente del 1882 e del 1873. Tuttora vi sono molti numeri che si sanno esprimere mediante gli usuali simboli funzionali e che non si sa se siano trascendenti o no  (ve ne sono anche che non si sa neanche se siano irrazionali o no: vedi).
    Per citare due esempi, ricordiamo che si è dimostrato solo, rispettivamente, nel 1979 e nel 2003 che  2^√2  e che  π/atan(1/2)  sono trascendenti.
    Osserviamo, per finire, che la terminologia con cui vengono classificati i numeri e le funzioni ha un'origine storica, legata a un periodo in cui le conoscenze e gli usi della matematica era molto limitati rispetto agli attuali, e non deve essere confusa con i significati che "elementare", "trascendente", … hanno in altri ambiti.  Ricordiamo, per esempio, i numeri non trascendenti ora richiamati e la funzione fattoriale che non è una funzione elementare.

Esercizio   (e  soluzione)