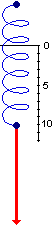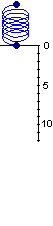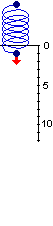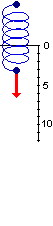L'integrazione

  L'integrazione studia, in generale, problemi di vario genere,  da come  • calcolare l'area di una figura a contorno non poligonale,  a come  • risalire al grafico di una funzione che rappresenta la posizione di un oggetto a partire da quello della sua velocità  a come  • calcolare la probabiltà che una certa variabile casuale continua, di cui sia nota la distribuzione, possa assumere valori compresi tra due numeri fissati,  a come  • determinare il lavoro di una forza di cui sia noto come varia l'intensità al variare del punto di applicazione.  Prima di considerare più a fondo il primo problema vengono discussi gli altri tre, per arrivare poi a una generalizzazione e sistemazione.  Segue un approfondimento dei legami tra integrazione e derivazione attraverso la messa a fuoco del teorema fondamentale del calcolo integrale.  Sono, infine, svolti alcuni approfondimenti.
    Quanto presentato qui è sufficiente per avere un quadro esauriente del concetto di "integrazione".  Altri aspetti e questioni riferite ad alcuni particolari insiemi di funzioni sono discusse nella voce  ancora sull'integrazione.  Alcune tecniche particolari saranno approfondite in  calcolo di integrali.
    Chi abbia già conoscenza dei concetti può saltare i "tre problemi introduttivi" e andare direttamente a generalizzazione e sistemazione.

  Tre problemi introduttivi

Primo problema

v = s' (m/s)       s (m)   t  (s)

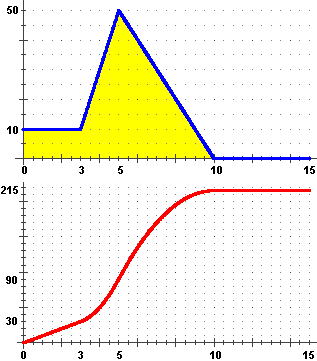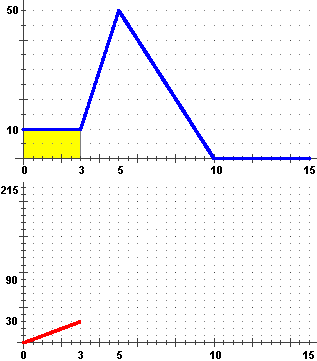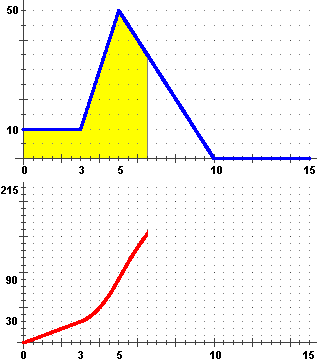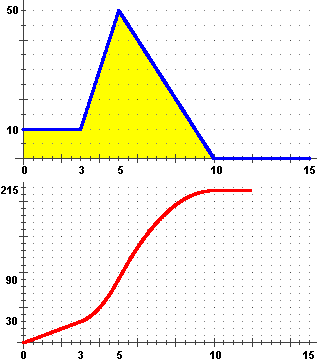
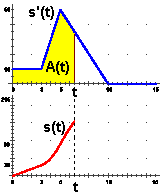
Dal grafico della  velocità (in m/s) v in funzione del tempo (in s) t come posso risalire al grafico della strada percorsa (in m) s in funzione di t ?     Intuisco che il grafico di s raffigurato a sinistra, sotto a quello di v, sia corretto;  v non è altro che la derivata s' di s e il grafico di v (quello sopra) sembra rappresentare come varia la pendenza lungo il grafico di s (quello sotto):  inizialmente questo ha pendenza costante (30/3 = 10),  poi sale con la concavità verso l'alto, ossia con pendenza via via crescente,  fino a t=5, in cui la pendenza inizia a diminuire,  fino ad arrivare a t=10, in cui la pendenza diventa nulla.     Si intuisce pure che il grafico di s in funzione di t rappresenta anche come varia l'area A delimitata dal grafico di v (ovvero di s'):

  Secondo problema

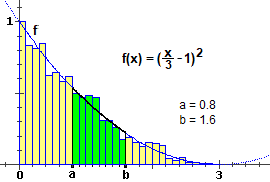
Ho verificato che l'istogramma della distribuzione statistica U tra 0 e 3 di una variabile casuale è approssimabile col grafico della funzione f: x → (x/3-1)².     Per calcolare la probabilità che U cada in un intervallo [a,b] potrei calcolare l'area compresa tra tale intervallo e il grafico di f come illustrato a fianco.     C'è un modo per calcolare l'area a partire dal termine (x/3-1)² ?

  Terzo problema

Abbiamo visto ( proporzionalità inversa) che il lavoro di una forza costante è dato dal prodotto di questa per lo spostamento che ha generato nella sua stessa direzione, come richiamato nel caso illustrato sotto a sinistra.
    Che dire nel caso che la forza cambi intensità, come nel caso ilustrato a destra, in cui la forza da esercitare per allungare la molla man mano aumenta, o in altre situazioni in cui la forza da esercitare F(s) cambia man mano che ci si sposta di s dalla posizione iniziale?

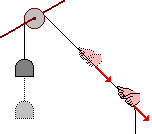
L = F · s

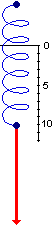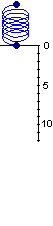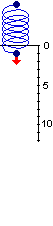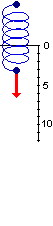cm ?

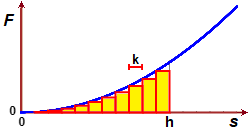
Suppomiamo di dover calcolare il lavoro per produrre lo spostamento h nel caso in cui la forza da vincere vari come nel caso illustrato nella figura qui a destra.     Potrei spezzare lo spostamento h in tanti piccoli spostamenti lunghi k e in ciascuno fare il prodotto tra la forza all'inizio di esso e k. La somma di questi prodotti, rappresentata nella figura dalla somma dei rettangolini, mi consente di approssimare il lavoro complessivo.     Il valore esatto del lavoro è rappresentato dall'area che sta sotto al grafico tra 0 e h.     Come calcolare esattamente questa area?

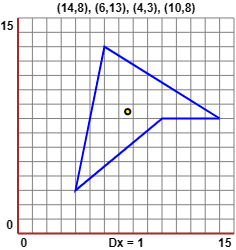
Generalizzazione e sistemazione     Abbiamo già visto alla voce  area come calcolare l'area di una figura poligonale facendo la somma delle aree dei triangoli in cui può essere scomposta, e abbiamo visto come questo procedimento può essere automatizzato con lo script "area polig".     Nel caso del poligono raffigurato a fianco otteniamo: nx = 4 14, 6, 4, 10 ny = 4 8, 13, 3, 8 area = 35 perim = 31.44226983514883 xcenter = 7.619047619047619 ycenter = 8.476190476190476

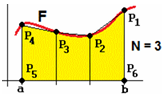In modo del tutto simile possiamo calcolare l'area che sta tra il grafico di una funzione F e l'asse delle x, per x che varia tra a e b, approssimando questa con l'area del poligono P1P2…P6 ottenuto suddividendo [a,b] in 3 parti uguali,  chiamando P1, P2, P3 e P4, in verso antiorario, i punti corrispondenti del grafico  e chiamando  P5 e P6 i punti dell'asse x di ascissa a e b,  e, in generale,  considerando N parti invece di 3.     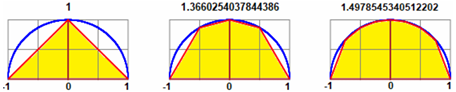Vediamo come potremmo ritrovare l'area del semicerchio che sta sotto al grafico di G: x → √(1-x²).  Aumentando il numero delle parti ci avvicineremmo sempre più a π/2 = 1.570796…

Abbiamo visto ( continuità) che se una funzione è continua in un intervallo [a,b] all'infittire degli input gli output sono man mano più fitti,  cioè al tendere a 0 della distanza tra due qualunque input anche la distanza tra i loro output tende a 0.  Nel caso della funzione F raffigurata sopra abbiamo che la striscia al cui interno sta il grafico di F, e che contiene la poligonale che approssima il grafico, ha spessore che all'aumentare di N tende a 0.  Quindi l'area del poligono, all'aumentare di N si stabilizza su un numero reale, che assumiamo come valore dell'area sottesa al grafico di F.

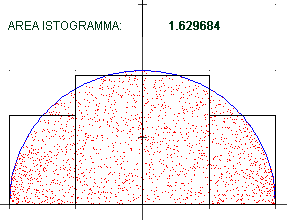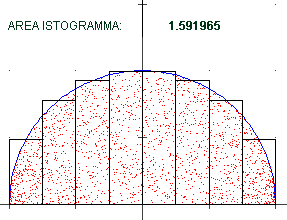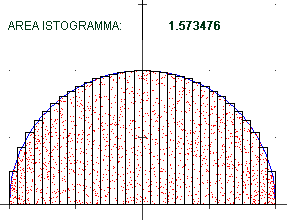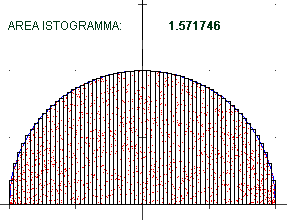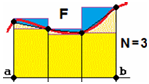
		Invece che congiungere i vertici ottenendo una poligonale avrei potuto prendere rettangolini aventi per altezza il valore della funzione nel centro di essi, come nella figura qui a fianco, relativa alla stessa funzione G considerata sopra:  abbiamo una sequenza di istogrammi la cui area è una successione di valori che anche in questo caso tende a π/2.

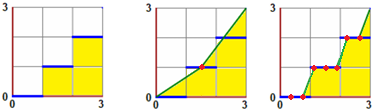    La figura sopra a destra illustra il caso di una funzione definita in un intervallo che è l'unione di intervallini in cui la funzione è continua e limitata;  quella qui rappresentata è la funzione parte intera, ma potrebbe essere anche un'altra funzione "continua a tratti".  La figura al centro visualizza che cosa si ottiene col primo procedimento per N=2,  la figura a destra visualizza ciò che si ottiene per N=8.

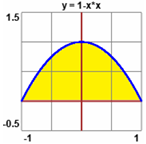
Lo script "integrali" automatizza il procedimento della ricerca dell'area delimitata da una funzione polinomiale o una potenza di essa attraverso l'approssimazione del suo grafico con un istogramma man mano più fitto.  Il nome "integrali" dello script richiama il fatto che il calcolo dell'area tra un grafico e l'asse x si chiama integrazione.  Su questo ritorneremo tra poco.     Vediamo come con questo script possiamo calcolare l'area tra la parabola y = 1-x² (raffigurata a destra) e l'asse x.  Sappiamo che l'area deve essere di poco maggiore di quella del triangolo avente la stessa base e altezza 1, ossia deve essere un po' più grande di 1.  Ecco alcune uscite:

2 n = 1 1.5 n = 2 1.375 n = 4 1.3333333399999985 n = 1e4 1.333333333750011 n = 4e4 1.3333333333593749 n = 16e4 1.3333333333349628 n = 64e4

    Si intuisce facilmente che l'area deve essere uguale a 1+1/3, ossia 3/3+1/3 = 4/3.

    Rivediamo il caso del semicerchio:

1.5707968138960287 n = 1e4 1.5707963876831614 n = 4e4 1.5707963344059523 n = 16e4 1.5707963277462433 n = 64e4 1.570796326913793 n = 256e4

    Fermandomi qui posso prendere l'approssimazione 1.570796327 (e so che π/2 = 1.570796326794896…).

Consideriamo anche il "secondo problema" iniziale. Se nello script metto 0.333333333333333 in q, -1 in u e 2 in e per n=400000 ottengo 0.2927407407407058 (che posso interpretare come 0.2927407407407... = 988/3375), in accordo con la stima fattibile osservando il grafico e usando la formula per l'area del trapezio.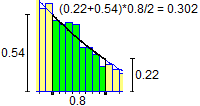

    Se provo con la funzione H: x → x tra -2 e 2 che cosa ottengo?

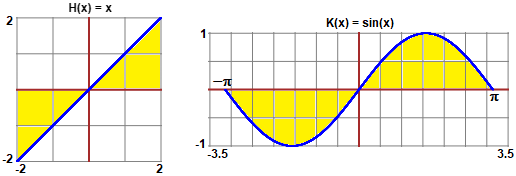
    Con n = 2, 4, 8, 16, 32, ... ottengo sempre 0 (con n = 1000 otterrei 7.638...·10^-17 a causa degli arrotondamenti). Come mai? L'integrazione calcola le aree orientate:  positive se stanno sopra all'asse x, negative se stanno sotto ad esso, e le "aree" a destra e a sinistra dell'asse y sono uguali in valore assoluto ma hanno segni opposti.

    Analogamente vale 0 l'area orientata tra -π e π di K: x → sin(x), di cui sopra a destra è tracciato il grafico.

    Dato un intervallo finito [a,b] e una funzione F che sia continua in [a,b],  o che sia ivi limitata e continua in un insieme finito di intervalli la cui unione sia [a,b],  l'area orientata tra grafico di F ed asse x viene chiamata  integrale di F tra a e b  e indicata  ∫ _{[a, b]} F  o  ∫_a^b F  o, per comodità,  _a ∫ ^b F.

    Se la funzione F è descritta esplicitamente si usa una notazione in cui compare un nome per la variabile.  Ad esempio nel caso precedente posso scrivere  _-1 ∫ ¹ x dx, o, volendo,  _-1 ∫ ¹ u du, _-1 ∫ ¹ t dt, … impiegando un nome di variabile differente.
    Nel caso di "sin" posso usare sia  _-π ∫ ^π sin(x) dx  che  _-π ∫ ^π sin,   ∫_[-π,π] sin, ...

    Il simbolo  ∫  ha la forma di una "S" allungata. Infatti ricorda che l'area che sta sotto alla curva può essere approssimata sommando opportuni rettangoli o trapezi.

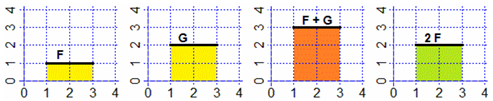
    La figura seguente illustra due proprietà degli integrali, simili a proprietà che abbiamo visto per le derivate, che useremo spesso (k è un numero reale):

∫ _[a,b] (F+G) = ∫ _[a,b] F + ∫ _[a,b] G       ∫ _[a,b] (k F) = k ∫ _[a,b] F

Esercizi:     uno     soluz.     due     soluz.     tre     soluz.
 

  Formula fondamentale del calcolo integrale

    Costruire approssimazioni successive, man mano più precise, è un operazione comoda per calcolare singoli integrali, se si dispone di un mezzo di calcolo. Vedremo in questo paragrafo che in molte situazioni  (ma non in tutte)  si può ricorrere ad un metodo più semplice, che ci consente di valutare gli integrali utilizzando opportune formule. Nel paragrafo "approfondimenti" faremo qualche considerazione storica sull'origine di questo metodo.
    Illustriamo il metodo con un esempio.  Consideriamo la funzione x → m·x.  Sotto a sinistra ne è rappresentato il grafico.  Vediamo come determinare l'area della figura illustrata sotto a destra, ossia  ∫ _[a,b] m·x dx,  con una formula.

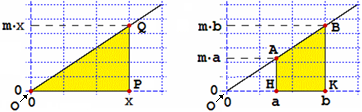
    L'area tra grafico ed asse orizzontale che va dall'ascissa 0 all'ascissa x è quella di un triangolo con base x ed altezza m·x, cioè 1/2·m·x².  Quella che va dall'ascissa a all'ascissa b è, evidentemente, la differenza tra l'area del triangolo BOK e quella del triangolo AOH:  1/2·m·x² −1/2·m·a².
    Ma D_x(1/2·m·x²) = m·x, ovvero 1/2·m·x² è un'antiderivata (rispetto ad x) di m·x.
    In definitiva ∫_[a,b] m·x dx = F(b)-F(a), dove F è un'antiderivata di x → m·x  (il concetto di antiderivata, o primitiva, di una funzione è stato introdotto nella voce  derivata e differenziale).

    La cosa potrebbe essere dimostrata in generale:

sia f continua in [a, b];  se  G' = f  allora  ∫_[a,b] f = G(b) - G(a)

    Questa proprietà viene chiamata formula fondamentale del calcolo integrale.

    Proviamo ad usare questo metodo per calcolare l'integrale tra -1 ed 1 di x → 1-x², che abbiamo visto valere 4/3.  Un'antiderivata di questa funzione è G: x → x-x³/3 (la derivata, rispetto ad x, di x è 1 e di x³/3 è 3·x²/3 = x²); G(1)-G(-1) = 1-1/3 - (-1+1/3) = 2-2/3 = 1+1/3 = 4/3.  OK!

  Approfondimenti

    A causa del legame tra derivazione e integrazione (espresso dal teorema fondamentale) si è presto diffuso l'uso di  ∫ f(x) dx  per indicare un generico termine g(x) tale che g'(x) = f(x);  l'operazione che ad f(x) associa tale termine viene chiamata  (oltre che antiderivazione)  integrazione indefinita, mentre l'aggettivo definita viene riservato all'associazione alla funzione e ad un intervallo [a, b] del numero ∫ _{[a, b]} f.
    È un uso che sopravvive per motivi storici, ma che è abbastanza ambiguo, e usato in modi differenti. Per chi lo affronta per la prima volta è bene, dunque, fare alcune osservazioni:
•  nel caso dell'integrale definito la variabile "integrata" è muta : si potrebbe scrivere  ∫ _{[-1, 3]} f(x) dx  o  ∫ _{[-1, 3]} f(t) dt  o  ∫ _{[-1, 3]} f,  o usare una variabile diversa da x e t  in modo del tutto equivalente;  invece  ∫ f(t) dt,  ∫ f(x) dx  e  ∫ f(u) du  indicano termini diversi;
•  qualcuno usa l'integrale indefinito per indicare un insieme di termini:  ∫ f(x) dx = {g(x) + c / c numero reale}:  ad es.  ∫ 6x dx  starebbe per l'insieme costituito dai termini  3x²,  3x² + 1,  3x² + 2/3,  3x² − 5, …, ovvero dai termini del tipo  3x² + c  al variare di c in IR,  altri (come noi faremo) un termine particolare che abbia come derivata  f(x);
•  noi useremo quest'ultima convenzione, ogni tanto esplicitando, e ogni tanto no, la possibilità di aggiungere una costante, ossia qualche volta scriveremo  ∫ 6x dx = 3x² e qualche altra volta  ∫ 6x dx = 3x² + c  lasciando al lettore la comprensione. Anche il software a volte usa una convenzione a volte l'altra. Ecco, ad esempio, due diverse uscite di WolframAlpha (vedi):

    Le prime due colonne della tabella seguente, e i primi quattro elementi delle terza, riassumono alcune derivate e alcuni integrali d'uso comune, che è bene pian piano incominciare a memorizzare.  Gli elementi successivi delle terza colonna possono essere consultati all'occorrenza; è, comunque, un buon esercizio verificare che le derivate di essi sono gli elementi della prima.

∫ g(x) dx	g(x)
f(x)	f '(x)	∫ f(x) dx
k xn  1/x  ex log(x) ax  (a > 0, a ≠ 1)  loga(x)  (a > 0, a ≠ 1) sin(x) cos(x)  tan(x)   asin(x)   acos(x)   atan(x)	0 n xn−1 −x−2 ex 1/x ax log(a) 1 / x / log(a) cos(x) −sin(x) cos(x)−2  [= 1+tan(x)²] 1 / √(1−x2) −1 / √(1−x2) 1 / (1+x2)	kx xn+1/(n+1)   (se n ≠ −1)  log(x) ,   log(−x)  ex x log(x) − x ax / log(a) (x log(x) − x) / log(a) −cos(x) sin(x) −log(cos(x)) ,   −log(−cos(x)) x asin(x) + √(1−x2) x acos(x) − √(1−x2) x atan(x) − log(1+x2)/2

    Con WolframAlpha possiamo usare anche i comandi  compute integral  e  compute derivative.

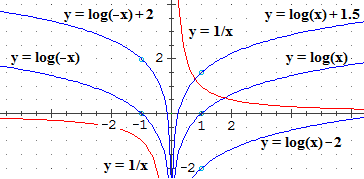
Si noti che come integrale di  1/x  si sono messe due espressioni:  log(x) e log(-x).  È da intendersi che la funzione che ad x positivo associa  log(x) + h  e che a x negativo associa  log(−x) + k,  dove h e k sono numeri reali qualunque, ha come derivata 1/x.  Infatti  per x>0  d (log(x)+h) / dx = d log(x) / dx+ d h / dx = 1/x  e  per x<0  d (log(−x)+k) / dx = d log(−x) / dx+ d k / dx = −1/x·( −1) = 1/x.     Considerazione analoghe valgono per altre funzioni: nella tabella è descritto il caso di  tan(x).     Esercizio.  Trovare  ∫ (ex + x−2 + x + 3) dx.     Cerco f tale che df / dx = ex + x−2 + x + 3.

Basta che f sia la somma delle funzioni che in x hanno come derivate  ex,  x−2,  x  e  3.     dex / dx = ex,  d − x−1 / dx = x−2,  d (x2/2) / dx = x,  d 3x / dx = 3 dx / dx = 3·1 = 3.     Quindi va bene  f(x) = ex − x−1 + x2/2 + 3x     e, più in generale,  f(x) = ex − x−1 + x2/2 + 3x + c  al variare di c in IR.