 caso discreto.
caso discreto.
Leggi di distribuzione (variabili continue)
Per una introduzione all'argomento rinviamo al primo paragrafo della analoga voce relativa al
 caso discreto.
caso discreto.
 Funzioni di densità e variabili casuali continue
Funzioni di densità e variabili casuali continue
Per mettere a fuoco il tema partiamo con un esempio concreto:
| Una azienda produce pere Abate. La pere prodotte sono di varia misura (il peso va da poco più di un etto a quasi tre etti) e sono commercializzate sia "sfuse" che in confezioni "da 4 hg" composte da due pere. La legge richiede che una confezione venduta come "da 4 hg" contenga "almeno" 4 hg; quindi la azienda, per queste confezioni, seleziona pere con peso maggiore o uguale a 200 g e inferiore 210 g. Supponiamo che in questo intervallo le pere prodotte si distribuiscano uniformemente. |
Questa è una situazione "realistica", anche se (per facilitare le elaborazioni e mettere meglio in luce come avviene la modellizzazione) è stata inventata. Di fronte ad essa possiamo porci problemi come i seguenti:
(1) Qual è il peso medio di una confezione da "4 hg"?
(2) Qual è la probabilità che una di queste confezioni
ecceda il peso di 4 hg per meno di 8 g?
(3) E che lo ecceda per più di 12 g?
Modellizziamo la situazione utilizzando opportune variabili casuali.
Se indico con P1 il peso in decine di grammi di una pera e con P2
quello dell'altra, il peso (netto) in decine di grammi di una confezione posso rappresentarlo con P, avendo posto
So che P1 e P2 variano in
Il fenomeno è analogo a quello del lancio di  due dadi equi: essi hanno uscite U1 e U2 distribuite uniformemente, la loro somma U no
(2 e 12 sono le uscite più improbabili, 7 è l'uscita più probabile).
due dadi equi: essi hanno uscite U1 e U2 distribuite uniformemente, la loro somma U no
(2 e 12 sono le uscite più improbabili, 7 è l'uscita più probabile).
Modellizzata la situazione possiamo studiarla sperimentalmente simulandola mediante il
 generatore di numeri casuali.
Supponiamo di impiegare un linguaggio di programmazione in cui esso sia indicato con Rnd, possiamo simulare sia P1 che P2 con
generatore di numeri casuali.
Supponiamo di impiegare un linguaggio di programmazione in cui esso sia indicato con Rnd, possiamo simulare sia P1 che P2 con
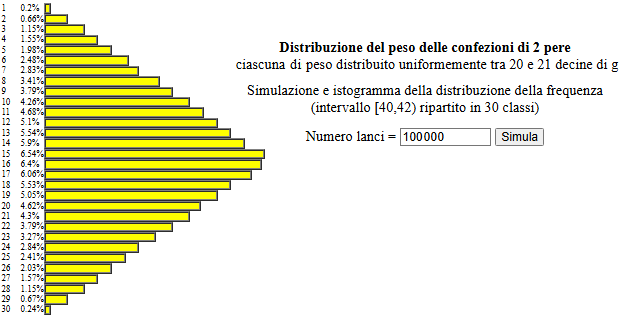
Si vede che l'istogramma delle frequenze relative tende a disporsi lungo un triangolo, analogamente
a quanto accadeva per i due dadi. Ma ora la variabile casuale P può assumere tutti i valori
di un intervallo, non un insieme di valori isolati come accadeva per U. La distribuzione teorica di P non potremo
rappresentarla con un istogramma, come nel caso della  distribuzione di una variabile discreta.
distribuzione di una variabile discreta.
 Poniamoci, dunque, il problema di
come rappresentare graficamente la legge di distribuzione di una Poniamoci, dunque, il problema di
come rappresentare graficamente la legge di distribuzione di una  variabile casuale continua.
variabile casuale continua.Partiamo dalla rappresentazione di una variabile continua X con distribuzione uniforme in |
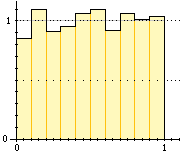 |
Sopra a destra è illustrato un esempio di quello che si può ottenere con 1000 prove
suddividendo [0,1) in 10 intervallini. Come altezze delle colonne sono state prese le densità di frequenza,
ovvero le frequenze relative divise per l'ampiezza degli intervallini  Distribuzione),
Distribuzione),
Il contorno superiore è il segmento con ordinata 1
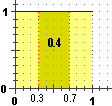
e ascissa che varia tra 0 e 1. La probabilità che X cada tra 0.3 e 0.7 posso interpretarla (vedi figura sottostante a sinistra)
come l'area della figura che sta tra tale segmento, l'asse delle ascisse e le rette verticali di ascissa 0.3 e 0.7,
area che vale
 |
 |
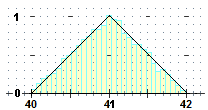 |
| X = Rnd | X = X1+X2, Xi = Rnd | P = P1+P2 |
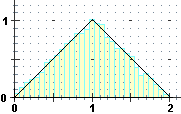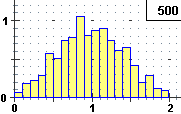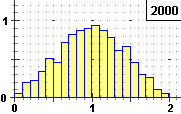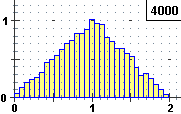
Nel caso di X somma di due variabili continue uniformi, e in particolare X = X1+X2 con X1 e X2 distribuite uniformemente
in [0,1), otteniamo istogrammi
che tendono a disporsi lungo un contorno triangolare, proprio come abbiamo trovato per il caso delle  pere abate:
sopra al centro quello che si ottiene per X, a destro quello che si ottiene per P.
pere abate:
sopra al centro quello che si ottiene per X, a destro quello che si ottiene per P.
 Consideriamo un'ulteriore situazione
problematica:
Consideriamo un'ulteriore situazione
problematica:
| L'organizzazione di vendite televisive Ventel riceve ordinazioni telefoniche tra le 14 e le 15. Per stabilire se il numero delle linee (e delle centraliniste) che impiega è conveniente fa studiare dalla ditta specializzata in statisiche Sifanstat i tempi di arrivo delle telefonate che arrivano ai centralini e le durate delle telefonate che riescono a prendere la linea. |
Nei file durata.htm e diff_t.htm sono riportate
le durate in secondi di 500 telefonate e 500 valori della distanza in secondi tra il tempo di arrivo di una telefonata e quello della precedente.
Prova ad analizzare con lo script "istogramma" (presente QUI)
i due file e verifica se ottieni esiti come i seguenti:
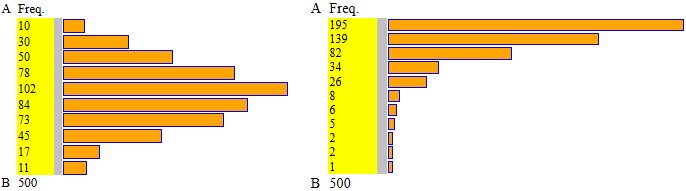
| A=0, B=100, 10 intervalli ampi 10 min=1.36, max=99.483, media = 48.403884 mediana=47.562, 1^|3^ quarto = 34.488|61.926 |
A=0, B=55, 11 intervalli ampi 5 min=1, max=50, media=8.626 mediana=6, 1^|3^ quarto = 3|12 |
Prova anche ad analizzarli con lo script "boxplot", ottenendo esiti come questi:
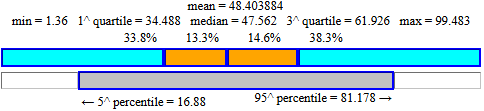

La ditta Sifanstat sa come approssimare gli istogrammi precedenti con delle curve che racchiudono con l'asse x un'area ampia 1, come nel caso del quadrato di base (0,1) e altezza 1 e il triangolo di base (0,2) e altezza 1 considerati sopra:
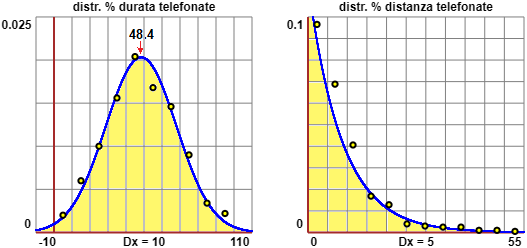
Come la ditta ha trovato queste funzioni lo vedremo più avanti. Osserviamo che possiamo convicerci che l'area "sottesa" sia 1 considerando le figure seguenti: 10·0.02/2 = 1, 20·0.1/2 = 1.
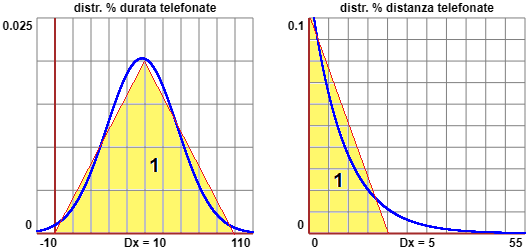
Funzioni come queste, e come
 quelle sul cui grafico si stabilizzavano gli istogrammi sperimentali di una distribuzione uniforme e della sommma di due distribuzioni unformi uguali,
si chiamano funzioni di densità. Il nome deriva dal fatto che i valori di queste funzioni rappresentano le densità di frequenza teoriche.
quelle sul cui grafico si stabilizzavano gli istogrammi sperimentali di una distribuzione uniforme e della sommma di due distribuzioni unformi uguali,
si chiamano funzioni di densità. Il nome deriva dal fatto che i valori di queste funzioni rappresentano le densità di frequenza teoriche.

Esercizio 1 (soluzione) Esercizio 2 (soluzione) Esercizio 3 (soluzione)
 Media e scarto quadratico medio teorici
Media e scarto quadratico medio teorici
Il concetto di  integrale
ci consente di approfondire e generalizzare quanto visto nei punti precedenti.
integrale
ci consente di approfondire e generalizzare quanto visto nei punti precedenti.
Se la variabile casuale U a valori nell'intervallo I ha istogrammi sperimentali che (all'aumentare delle prove e al ridurre l'ampiezza degli intervallini in cui viene ripartito I) hanno contorno superiore che tende a condondersi col grafico di una funzione f con dominio I, se f è integrabile su I posso porre, per ogni a e b in I:
Pr ( a ≤ U ≤ b ) =
Nota questa funzione, quindi, possiamo calcolare Pr(U∈J) per ogni intervallo J che sta nel dominio di U. f è dunque una caratterizzazione della legge di distribuzione di U. Come abbiamo anticipato nei paragrafi precedenti, f viene chiamata densità di probabilità [della legge di distribuzione] di U.
Ci occupiamo, nel seguito, di una variabile casuale U a valori in un intervallo di I per cui esista una funzione di densità f (non è detto che una tale f esista; quando parleremo di "variabile casuale continua" sottintenderemo che una tale f esista).
 Sia f la densità di U. Posso definire la media M(U) di U in analogia al caso discreto:
Sia f la densità di U. Posso definire la media M(U) di U in analogia al caso discreto:
Per lo  scarto quadratico medio abbiamo sqm(U) = √Var(U), dove, posto
scarto quadratico medio abbiamo sqm(U) = √Var(U), dove, posto
Var(U) = M(U - μ)2 =
[come per M(U) con al posto dei valori x di U i valori x-μ di U-μ]
 Consideriamo le variabili casuali continue finora introdotte:
Consideriamo le variabili casuali continue finora introdotte:
|
• Distribuzione uniforme in [0,1); densità: f(x) = 1. (vedi) μ = 0∫1 x·f(x) dx = 0∫1 x dx = [x2/2]x=1 − [x2/2]x=0 = 1/2 Var = 0∫1(x - m)2 f(x) dx =
0∫1(x - 1/2)2 dx =
Vediamo come calcolare l'ultimo integrale con lo script "integrali": |  |
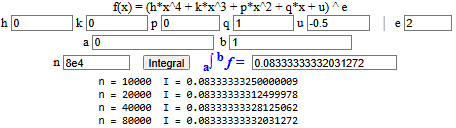
Volendo studiare la varibile casuale sperimentalemente, con "n. casuali reali" e con "calcolatrice2":

• Distribuzione uniforme in [a,b):
è la legge considerata sopra, con, rispetto ad essa, uscite moltiplicate per
• Distribuzione esponenziale; densità: f(x) = a e− a x, con a > 0 (è una delle due distribuzioni viste qui, per un a fissato)
μ = 0∫∞ x·f(x) dx = 0∫∞ x ae-ax dx = 1/a 0∫-∞ueu du = 1/a (per i calcoli vedi questo esercizio)
sqm = √( 0∫∞(x - 1/a)2 ae-ax dx ) = √(1/a2) = 1/a = μ
Nel caso dell'esempio visto sopra la media m era il tempo medio tra una telefonata e la telefonata successiva. Hanno andamento simile le distribuzioni sperimentali dei tempi di attesa tra un arrivo e l'arrivo successivo di molti fenomeni (ad esempio della distanza temporale tra la venuta al semaforo di un'auto e la venuta dell'auto successiva, nel caso di semafori preceduti da un lungo tratto di strada senza altri impedimenti al traffico programmati dall'uomo; il parametro a, ossia il reciproco del tempo medio, in inglese viene chiamate rate, ossia "velocità").
• La distribuzione della durata delle telefonate ha una forma particolare, che assomiglia a quella di certe distribuzioni binomiali ( caso discreto): è una particolare
distribuzione gaussiana, la cui forma è caratterizzata dai valori della media e dello
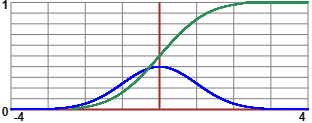
scarto quadratico medio (o deviazione standard). Sotto a sinistra è rappresentato il grafico della gaussiana di media 0 e sqm 1.
La sua equazione è la seguente:
caso discreto): è una particolare
distribuzione gaussiana, la cui forma è caratterizzata dai valori della media e dello
scarto quadratico medio (o deviazione standard). Sotto a sinistra è rappresentato il grafico della gaussiana di media 0 e sqm 1.
La sua equazione è la seguente:
| f(x) = |
1 | e |
| (-∞ < x < ∞) |
||||
| —— | ||||||||
| √(2π) |
Dato che f(-x) = f(x), la curva è simmetrica rispetto all'asse y e quindi:
| media = | −∞ ∫ −∞ | x f(x) dx = 0 |
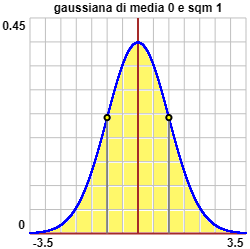 |  |
Lo script "gaussiana" presente QUI ci permette di calcolare la densità delle distribuzioni gaussiane. Verifichiamo con essa che effettivamente l'integrale tra -∞ e ∞ della gaussiana di media 0 e sqm 1 vale 1:

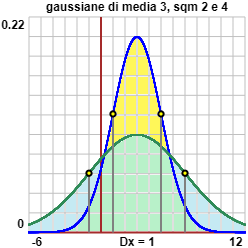
A destra sono rappresentate la distribuzione gaussiana di media 3 e sqm 2 e quella di sqm 4. Sono rappresentate dalla formula seguente, in cui "s" rappresenta lo sqm (o deviazione standard):
| densità: f(x) = |
1 | e |
| |||||||
| ——— | ||||||||||
| √(2π) s |
Ecco come è stato realizzato l'ultimo grafico.
Utilizzzando nuovamente lo script "gaussiana" ottengo:
| a∫b g = | 1 | if a=-inf b=inf, | m=0 s=1 |
| a∫b g = | 0.68268949234 | if a=-1 b=1, | m=0 s=1 |
| a∫b g = | 1 | if a=-inf b=inf, | m=3 s=4 |
| a∫b g = | 0.68268949234 | if a=-1 b=7 | m=3 s=4 |
| a∫b g = | 0.68268949234 | if a=1 b=5 | m=3 s=2 |
Potevo usare anche WolframAlpha. Esempio:

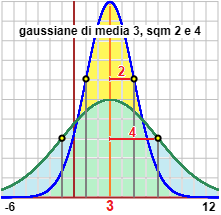 | Osserviamo, infine, che nei punti di ascissa media+sqm e media-sqm il grafico della funzione ha un
cambiamento di concavità, ovvero che essi sono dei punti di flesso ( Nel caso della gaussaina di media 0 e sqm 1 sono i punti di ascissa -1 ed 1. solve d^2/dx^2 1/sqrt(2*PI)*exp(-x^2/2) = 0 → x = ± 1 |
Possiamo dire che lo scarto quadratico medio, nel caso della densità gaussiana, è un indicatore della dispersione:
 limiti
limiti
 Soffermiamoci sulla distribuzione
gaussiana. Il suo nome deriva dal matematico (o fisico, naturalista, filosofo, …: le etichette
attuali avevano un significato diverso un paio di secoli fa) Gauss, che la studiò
particolarmente agli inizi dell'Ottocento; essa, in realtà, fu introdotta nel calcolo delle
probabiltà almeno una settantina d'anni prima; è nota anche come distribuzione
normale.
Vediamo un primo esempio d'uso di questa legge di distribuzione, sulla quale
torneremo più avanti, e di tale programma di calcolo.
Soffermiamoci sulla distribuzione
gaussiana. Il suo nome deriva dal matematico (o fisico, naturalista, filosofo, …: le etichette
attuali avevano un significato diverso un paio di secoli fa) Gauss, che la studiò
particolarmente agli inizi dell'Ottocento; essa, in realtà, fu introdotta nel calcolo delle
probabiltà almeno una settantina d'anni prima; è nota anche come distribuzione
normale.
Vediamo un primo esempio d'uso di questa legge di distribuzione, sulla quale
torneremo più avanti, e di tale programma di calcolo.
La probabilità che un prodotto di un certo tipo sia difettoso è 1%. Qual è la probabilità che tra 10000 pezzi scelti a caso non ve ne siano più di 70 difettosi?
È un problema che dovrebbe essere risolto usando la legge di distribuzione binomiale,
che abbiamo già considerato studiando le  variabili casuali discrete:
variabili casuali discrete:
Pr(N = k) = C(n,k) · pk · (1 – p)n-k.
Nel nostro caso devo calcolare Σk C(10000,k)·1%k·99%10000-k (k=0,…,70).
Usando WolframAlpha posso fare:
Ma, se non ho a disposizione un mezzo di calcolo potente, in questo caso,
come vedremo meglio in una voce successiva
 limiti
limiti variabili casuali discrete],
variabili casuali discrete],
Dopo aver calcolato con una calcolatrice √0.99 = 0.99498743710662 usando lo script "gaussiana" ottengo:
Ho integrato tra -0.5 e 70.5 in quanto, passando dal finito al caso continuo,
i valori 0 e 70 corrispondono agli intervalli
 La media e lo scarto quadratico medio di una distribuzione
gaussiana permettono di determinare completamente la distribuzione: sono i due parametri che identificano la particolare densità gaussiana.
La media e lo scarto quadratico medio di una distribuzione
gaussiana permettono di determinare completamente la distribuzione: sono i due parametri che identificano la particolare densità gaussiana.
Nel caso della distribuzione esponenziale la densità è caratterizzata da un solo parametro: il valore della media, che coincide con quello dello scarto quadratico medio.
La legge di distribuzione uniforme in un intervallo di estremi a e b è, invece, completamente determinata dai valori di a e b −
Media e scarto quadratico medio danno delle indicazioni sulla forma e sulla posizione del grafico della funzione densità, ma, se non si conosce la forma di esso, e non si è in casi particolari come i precedenti, non sono sufficienti a determinarla. Possono essere di aiuto altri valori, di cui ne vediamo alcuni.
|
Nel caso in cui U sia una variabile casuale che
può assumere valori in un intervallo I di numeri reali, la mediana di U è definita come nel caso discreto
Se U è continua, viene chiamata moda di U ogni numero x di I per cui f(x) è massimo. Ovviamente − come nel caso discreto
|
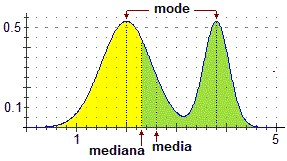 |
Il confronto tra i diversi indici di posizione, mentre nel caso discreto può dare indicazioni sulla forma dell'istogramma di distribuzione, nel caso continuo può dare indicazioni sulla forma del grafico della funzione di densità. Le considerazioni geometriche svolte nel caso discreto  valori
valori
Esercizio 4 (soluz.) Esercizio 5 (soluz.) Esercizio 6 (soluz.) Esercizio 7 (soluz.) Esercizio 8 (soluz.)
 Funzione di ripartizione
(o di distribuzione)
Funzione di ripartizione
(o di distribuzione)
Sotto sono riprodotti sia il grafico della funzione di distribuzione uniforme in
 valori medi - 2 e di cui si
è vista la rappresentazione grafica in un approfondimento (in
valori medi - 2 e di cui si
è vista la rappresentazione grafica in un approfondimento (in  questo).
questo).
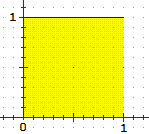 | 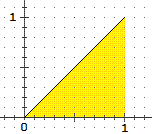 |
| la funzione di densità (teorica) di Rnd: x → 1 | la sua funzione di ripartizione: x → Pr(uscita < x) = x |
Se U è una densità, viene detta ripartizione (cumulative distribution function in inglese) di U la funzione
Si noti che, nel caso in cui U sia continua, come nei casi visti sopra,
per ogni x (appartenente al dominio di U)
La contraddizione è solo apparente. Da una parte, la probabilità complessiva
non è data da una somma, ma, nel caso di U che vari con continuità in un intervallo,
da un  integrale
integrale calcolo approssimato)
calcolo approssimato)
A volte si considera ripartizione di U è la funzione
Come ulteriore controllo possiamo tracciare il grafico della funzione densità
(dalla forma triangolare)
e quello della funzione di
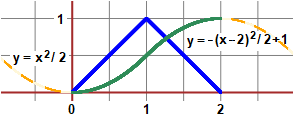
Nota. La funzione di ripartizione x → ∫ [−∞, x] h(t) dt
dove h è una gaussiana è una funzione non elementare
[ |
 |
 A differenza del caso finito,
non è detto che esista la media di una variabile aleatoria U (dotata di legge di distribuzione associata a una misura di probabilità Pr) nel caso continuo e nel caso discreto infinito.
A differenza del caso finito,
non è detto che esista la media di una variabile aleatoria U (dotata di legge di distribuzione associata a una misura di probabilità Pr) nel caso continuo e nel caso discreto infinito.
Ad esempio la variabile U a valori in (1,∞) con densità f(x)=1/x² (f è una densità in quanto
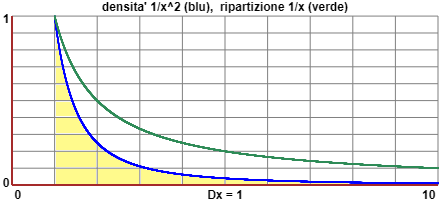
Analogamente se S è Σ 1/i² (i da 1 a ∞) e Pr(U=i) = 1/(S·i²) (i intero positivo), la variabile aleatoria (a valori interi positivi) U non ha media.
Mentre nel caso discreto esiste sempre almeno
una moda, nel caso continuo non è detto che esista. Ad esempio se f(x)=1/(2√x), f è una funzione di densità tra 0 e 1 (ivi l'integrale è 1) che non ha massimo.
Esercizio 9 (soluz.)
Esercizio 10 (soluz.)
Esercizio 11 (soluz.)
Esercizio 12 (soluz.)
Esercizio 13 (soluz.)